hdu 2363(枚举+最短路好题)

Cycling

Time Limit: 5000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1247    Accepted Submission(s): 411

Problem Description

You
want to cycle to a programming contest. The shortest route to the
contest might be over the tops of some mountains and through some
valleys. From past experience you know that you perform badly in
programming contests after experiencing large differences in altitude.
Therefore you decide to take the route that minimizes the altitude
difference, where the altitude difference of a route is the difference
between the maximum and the minimum height on the route. Your job is to
write a program that finds this route.
You are given:

the number of crossings and their altitudes, and

the roads by which these crossings are connected.
Your
program must find the route that minimizes the altitude difference
between the highest and the lowest point on the route. If there are
multiple possibilities, choose the shortest one.
For example:

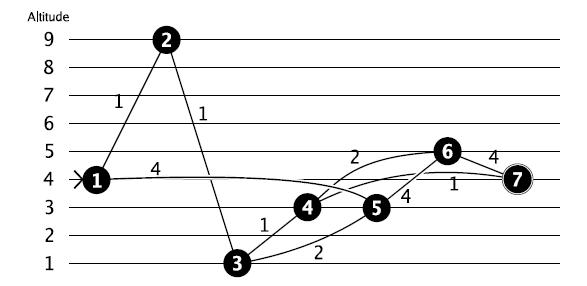
In
this case the shortest path from 1 to 7 would be through 2, 3 and 4,
but the altitude difference of that path is 8. So, you prefer to go
through 5, 6 and 4 for an altitude difference of 2. (Note that going
from 6 directly to 7 directly would have the same difference in
altitude, but the path would be longer!)

 

Input

On the first line an integer t (1 <= t <= 100): the number of test cases. Then for each test case:

One
line with two integers n (1 <= n <= 100) and m (0 <= m <=
5000): the number of crossings and the number of roads. The crossings
are numbered 1..n.

n lines with one integer hi (0 <= h_i <= 1 000 000 000): the altitude of the i-th crossing.

m lines with three integers a_j , b_j (1 <= a_j , b_j <= n) and c_j (1 <= c_j <= 1 000 000): this indicates that there is a two-way road between crossings a_j and b_j of length c_j . You may assume that the altitude on a road between two crossings changes linearly.
You
start at crossing 1 and the contest is at crossing n. It is guaranteed
that it is possible to reach the programming contest from your home.

 

Output

For each testcase, output one line with two integers separated by a single space:

the minimum altitude difference, and

the length of shortest path with this altitude difference.

 

Sample Input

1
7 9
4
9
1
3
3
5
4
1 2 1
2 3 1
3 4 1
4 7 1
1 5 4
5 6 4
6 7 4
5 3 2
6 4 2

 

Sample Output

2 11

 

题意:有n个点m条边,每个点都有一个高度,问在保证高度之差最小的情况下从1点到第n点，最小高度差和最短路分别是多少?

题解:这题做的时候完全没思路,一直在想两点之间的高度问题，怎样才能从子问题递推到父亲问题找到最优的解，后面还是不会,,,然后看了题解发现自己的思维太死板了。。这个题只要枚举所有的高度差，然后按照高度差排序，当在某个高度差的限制下我们能够达到第n点（当然这个时候路径上每个点都应该在low和high之间），那么这个结果就是我们要的结果。

#include <stdio.h>
#include <math.h>
#include <iostream>
#include <algorithm>
#include <math.h>
#include <queue>
#include <string.h>
using namespace std;
typedef long long ll;
const int N = ;
const int INF = ;
struct Node { ///枚举高度差所需要用到的结构体
    int low,high;
}node[N*N];
struct Edge{
    int v,w,next;
}edge[N*N];
int head[N];
ll h[N];
int graph[N][N];
int n,m;
int cmp(Node a,Node b){
    return (a.high-a.low)<(b.high-b.low);
}
bool vis[N];
int d[N];
void addEdge(int u,int v,int w,int &k){
    edge[k].v = v,edge[k].w = w;
    edge[k].next = head[u],head[u]=k++;
}
void spfa(int s,int low,int high){
    queue<int > q;
    for(int i=;i<=n;i++){
        d[i] = INF;
        vis[i] = false;
    }
    d[s] = ;
    q.push(s);
    while(!q.empty()){
        int u = q.front();
        q.pop();
        vis[u] = false;
        if(h[u]>high||h[u]<low) continue;
        for(int k = head[u];k!=-;k=edge[k].next){
            int v = edge[k].v,w = edge[k].w;
            if(h[v]>high||h[v]<low) continue;
            if(d[v]>d[u]+w){
                d[v] = d[u]+w;
                if(!vis[v]){
                    vis[v]=true;
                    q.push(v);
                }
            }
        }
    }
}
int main()
{
    int tcase;
    scanf("%d",&tcase);
    while(tcase--){
        memset(head,-,sizeof(head));
        scanf("%d%d",&n,&m);
        for(int i=;i<=n;i++){
            scanf("%lld",&h[i]);
        }
        int tot = ;
        for(int i=;i<=m;i++){
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            addEdge(a,b,c,tot);
            addEdge(b,a,c,tot);
        }
        int k = ;
        for(int i=;i<=n;i++){
            for(int j=i;j<=n;j++){
                if(h[i]<h[j]){
                    node[k].low = h[i];

                    node[k++].high = h[j];
                }
                else {
                    node[k].low = h[j];
                    node[k++].high = h[i];
                }
            }
        }
        sort(node,node+k,cmp);
        for(int i=;i<k;i++){
            spfa(,node[i].low,node[i].high);
            if(d[n]<INF){
                printf("%d %d\n",node[i].high-node[i].low,d[n]);
                break;
            }
        }
    }
}