Leetcode 529.扫雷游戏

扫雷游戏

让我们一起来玩扫雷游戏！

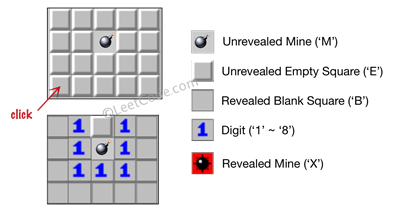
给定一个代表游戏板的二维字符矩阵。 'M' 代表一个未挖出的地雷，'E' 代表一个未挖出的空方块，'B' 代表没有相邻（上，下，左，右，和所有4个对角线）地雷的已挖出的空白方块，数字（'1' 到 '8'）表示有多少地雷与这块已挖出的方块相邻，'X' 则表示一个已挖出的地雷。

现在给出在所有未挖出的方块中（'M'或者'E'）的下一个点击位置（行和列索引），根据以下规则，返回相应位置被点击后对应的面板：

1. 如果一个地雷（'M'）被挖出，游戏就结束了- 把它改为 'X'。
2. 如果一个没有相邻地雷的空方块（'E'）被挖出，修改它为（'B'），并且所有和其相邻的方块都应该被递归地揭露。
3. 如果一个至少与一个地雷相邻的空方块（'E'）被挖出，修改它为数字（'1'到'8'），表示相邻地雷的数量。
4. 如果在此次点击中，若无更多方块可被揭露，则返回面板。

示例 1：

输入:

[['E', 'E', 'E', 'E', 'E'],

['E', 'E', 'M', 'E', 'E'],

['E', 'E', 'E', 'E', 'E'],

['E', 'E', 'E', 'E', 'E']]

Click : [3,0]

输出:

[['B', '1', 'E', '1', 'B'],

['B', '1', 'M', '1', 'B'],

['B', '1', '1', '1', 'B'],

['B', 'B', 'B', 'B', 'B']]

解释:

示例 2：

输入:

[['B', '1', 'E', '1', 'B'],

['B', '1', 'M', '1', 'B'],

['B', '1', '1', '1', 'B'],

['B', 'B', 'B', 'B', 'B']]

Click : [1,2]

输出:

[['B', '1', 'E', '1', 'B'],

['B', '1', 'X', '1', 'B'],

['B', '1', '1', '1', 'B'],

['B', 'B', 'B', 'B', 'B']]

解释:

注意：

1. 输入矩阵的宽和高的范围为 [1,50]。
2. 点击的位置只能是未被挖出的方块 ('M' 或者 'E')，这也意味着面板至少包含一个可点击的方块。
3. 输入面板不会是游戏结束的状态（即有地雷已被挖出）。
4. 简单起见，未提及的规则在这个问题中可被忽略。例如，当游戏结束时你不需要挖出所有地雷，考虑所有你可能赢得游戏或标记方块的情况。

思路

BFS，不能一直深搜，因为当前位置如果要显示数字（即周围有几个雷），那么不能对它的四周进行深搜。

因此先count当前四周雷数，如果没有雷才能继续递归搜索

 public class Solution {
     int[][] dirs = {{1, 0}, {1, 1}, {1, -1}, {-1, 0}, {-1, 1}, {-1, -1}, {0, 1}, {0, -1}};
     public char[][] updateBoard(char[][] board, int[] click) {
         if (board == null || board.length == 0) {
             return board;
         }
         int i = click[0];
         int j = click[1];
         if (board[i][j] == 'M') {
             board[i][j] = 'X';
             return board;
         }
         update(board, i, j);
         return board;
     }
     private void update(char[][] board, int i, int j) {
         if (board[i][j] != 'E') {
             return;
         }
         int cnt = 0;
         for (int[] dir : dirs) {
             int row = dir[0] + i;
             int col = dir[1] + j;
             if (row >= 0 && row < board.length && col >= 0 && col < board[0].length && board[row][col] == 'M') {
                 cnt++;
             }
         }
         board[i][j] = '*';
         if (cnt == 0) {
             board[i][j] = 'B';
             for (int[] dir : dirs) {
                 int row = dir[0] + i;
                 int col = dir[1] + j;
                 if (row >= 0 && row < board.length && col >= 0 && col < board[0].length) {
                     update(board, row, col);
                 }
             }
         } else {
             board[i][j] = (char) (cnt + '0');
         }
     }
 }