ACM学习历程—BestCoder 2015百度之星资格赛1006 单调区间（组合数学）

Problem Description

百小度最近在逛博客，然后发现了一个有趣的问题。

如下图所示，是一个12 
位数014326951987 
, 它的数字先逐渐变大, 然后变小，再变大，接着变小，又变大，最后变小。我们就称，其共包含6 
个单调区间。

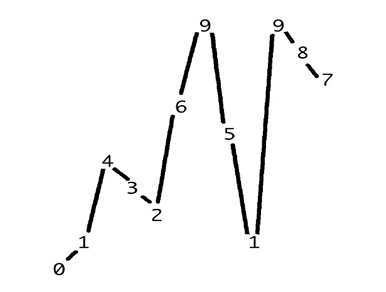
现在问题来了：一个n位数平均包含多少个单调区间？单调区间的平均长度又是多少？

因为我们考虑到这样的数样本太大，有10 n  
这么多，所以百小度决定缩小样本，假定任意两位相邻数字不能相同，而且这个n 
位数允许以0 
开头。现在我已经将样本大小已经被缩小到10∗9 n−1  
，接下来把这个问题交给你，请你开启大脑挖掘机，挖挖答案在哪里。

Input

第一行为T 
，表示输入数据组数。

下面T行，每行包含一个正整数n 
，n 
为不大于100000 
的正整数。

Output

对第i组数据，输出

Case #i:

然后输出两个实数，用空格隔开，分别为平均单调区间数和单调区间平均长度，结果保留六位小数。

Sample Input

2
2
12

Sample Output

Case #1:
1.000000 2.000000
Case #2:
8.037037 2.368664

原题是IMO候选题：

考虑这么一个  位数  ，如图所示，它的数字先逐渐变大，然后开始变小，再变大，再变小，再变大，再变小。我们就说，它一共包含了  个单调区间。我们的问题就是：一个 n 位数平均有多少个单调区间？为了避免歧义，我们假设任意两位相邻的数字都不相同，因而像  这样的数我们就不考虑了。另外，大家可能已经注意到了，我们允许这个 n 位数以数字  开头。因而，更精确地说，我们的问题是：相邻数字都不相同的、允许以  开头的所有 n 位数当中，平均有多少个单调区间？

    这个题目来自  年 IMO 候选题。

    让我们把所有这种 n 位数的个数记作 N 。那么 N 等于多少？这个 n 位数的第一位有  种选择，今后的每一位都只有  种选择（因为要跟前一位不一样），因而 n 位数一共有 N =  · 9n- 个。接下来，我们要求的就是，所有 n 位数当中的所有单调区间一共有多少个。我们换一种方法来累计这些单调区间：先算所有从第一位开始的单调区间，再算所有从第二位开始的单调区间，等等，最后算所有从第 n 位开始的单调区间。如果用 ri 来表示所有从第 i 位开始的单调区间的数目，那么我们要求的平均单调区间数就是 (r1 + r2 + … + rn) / N ，也就是 r1 / N + r2 / N + … + rn / N 。注意到其中的每一项 ri / N 其实就是从 N 个合法的 n 位数中任取一个后，存在以第 i 位数打头的单调区间的概率。因此，我们只需要求出这 n 个概率值，加起来便是我们想要的答案了。
    显然， r1 / N =  ，因为第一位数字必然会引领一个单调区间。显然， rn / N =  ，因为最后一位数字不可能引领一个新的单调区间。那么，对于其他的 ri / N 呢？注意到，第 i –  位、第 i 位和第 i +  位的大小关系一共可能有以下四种情况：

    其中，只有第三种情况和第四种情况下，第 i 位才会成为一个新的单调区间的开始。为了计算这两种情况发生的概率，我们只需要算出情况  和情况  发生的概率，再用  来减即可。情况  发生的概率有多大呢？三位数字串一共有  ·  个（第一位有  种选择，后面的每一位都只有  种选择，因为要跟前一位不一样）。为了得到递增的数字串，我们只需要选出三个不同的数字，然后把它们从小到大排列即可，这一共有 C(, ) 种方法。因此，情况  的发生概率就是 C(, ) / ( · ) = / 。同理，情况  的发生概率也是 / ，两者加起来就是 / ；反过来，情况  和情况  出现的概率就是  – / = / 了。
    因此，我们最终要求的答案就是  + / + / + … + / +  =  + (n – ) · / 。

    这个结论还会引出很多有意思的问题。在一个  位数当中，平均会产生  个单调区间。我们似乎发现了一个很不合理的地方：这岂不意味着，平均每个单调区间的长度只有 / = 1.45 个数字吗？考虑到单调区间的长度不可能恰好是 1.45 个数字，为了得到 1.45 这个平均长度，一定有些区间的长度比 1.45 小，有些区间的长度比 1.45 大。有些区间的长度比 1.45 小，这不就意味着这些区间的长度为  吗？而一个区间的长度显然是不可能为  的。怎么回事？
    其实， / = 1.45 这个算式是错的。在这  个单调区间中，除了最后一个区间以外，每一个区间的最后一个数与下一个区间的第一个数都是公共的。因此，这个  位数当中，有  个数被重复使用了。所以，在一个  位数当中，单调区间的平均长度应该是 ( + ) /  = 2.4 。
    类似的， n 位数的单调区间的平均长度为 (n + (/)(n – )) / ( + (/)(n – )) = (46n – ) / (19n – ) = ( – /n) / ( – /n) 。当 n 无穷大时，其极限为 / 。

参考资料：Ross Honsberger, From Erdos to Kiev: Problems of Olympiad Caliber, pp. -

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
#include <string>
#define LL long long

int main()
{
    //freopen("test.in", "r", stdin);
    int T, n;
    double ans;
    scanf("%d", &T);
    for (int times = ; times <= T; ++times)
    {
        printf("Case #%d:\n", times);
        scanf("%d", &n);
        ans =  + (n-2.0)*/;
        printf("%lf ", ans);
        ans = (-38.0/n) / (-11.0/n);
        printf("%lf\n", ans);
    }
    return ;
}