[洛谷P4556][BZOJ3307]雨天的尾巴-T3订正

线段树合并+树上差分

题目链接（···） 「简单」「一般」——其实「一般」也只多一个离散化

考试时想法看>这里<

总思路：先存所有的操作，离散化，然后用树上差分解决修改，用权值线段树维护每个值的个数，最后dfs合并处理答案（先处理儿子，再合并自己和儿子，递归解决）

简单版当然不用离散话辣。

做了好几天，感觉自己傻了。

但是好像也不是这样的

事实上，这道题确实扩充了我对线段树的认识。

它它它还可以不存左右区间的啊？——一定是我太蒻了

先附样例以示敬意

Sample Input

Sample Output

我还是第一次见这么恐怖的样例

不过它也是我的救命稻草，让我骗了5分，这是之前的事

样例以1为根的巨树

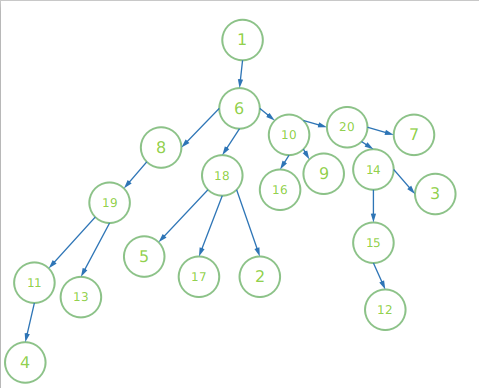
还是能看下的

树上差分就是通过修改树上某些节点的值来修改一段区间值的方法，比较常用

比如我们需要加树上一个区间

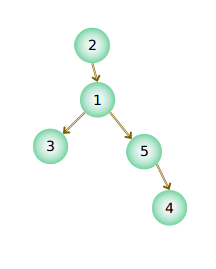想这样，加从3到4的区间，每个加1（加N也一样）

那么我们按照差分法，3++，4++，1--，2--

「公式」其实是 x+n ,y+n ,lca(x,y)-n ,father[lca(x,y)]-n

别告诉我你不会lca，虽然我也是刚学了实用的版本

结果是这样的

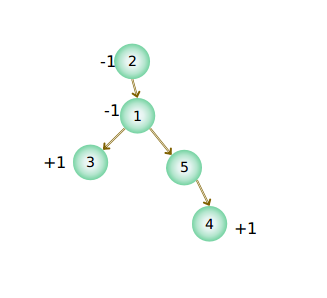这一步很快的···

我们要的结果当然不是±1什么的，要的是1或0

所以下面就是dfs统计结果（‘=’号前是过程，‘=’后是结果）

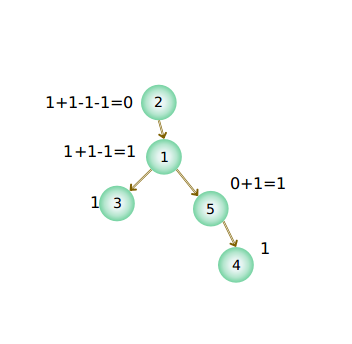仿佛得到了结果

这样我们就能够离线处理树上的区间加减

注意：只能是离线，N个修改，一次输出

---

线段树合并前面已经说过，这里不再细讲。

这个题仿佛对内存的限制很苛刻（我MLE 22 次，数过，想哭），所以线段树的节点一定要节约开空，只开最大值和左右儿子指针

//鬼知道我调了几天的是这个傻点

左右区间可以递归维护，不必要一定存在节点里，

也不必须在维护最大值时捆绑维护下标，查询时的O（NlogN）还是可以接受的

 #include <algorithm>
 #include <iostream>
 #include <cstring>
 #include <cstdlib>
 #include <cstdio>
 #include <cmath>
 #include <queue>
 #define  N 200001
 #define  B 2*N
 #define  logN 31
 using namespace std;
 struct ST{
     int f,t,next;
 };ST rs[B];
 int tot=,fl[N],n,m,len;
 void add(int f,int t){
     rs[tot].f=f;
     rs[tot].t=t;
     rs[tot].next=fl[f];
     fl[f]=tot;
     tot++;
 }
 struct XDS{
     XDS *lid,*rid;
     int maxn;
     XDS(){
         lid=rid=NULL;
         maxn=;
     }
 };XDS *root[N];
 struct CON{
     int x,y,z;
 };CON q[N];
 int val[N];
 int fvind(int i){
     return lower_bound(val,val+len,i)-val+;
 }
 inline void build(XDS *&n){
     n=new XDS();
 }
 void add(XDS *&rt,int v,int k,int l,int r){
     if(rt==NULL)build(rt);
     if(l==r){
         rt->maxn+=k;
         return ;
     }
     int mid=(l+r)>>;
     if(mid>=v){
         add(rt->lid,v,k,l,mid);
     }
     else{
         add(rt->rid,v,k,mid+,r);
     }
     if(rt->lid!=NULL){
         rt->maxn = rt->lid->maxn;
     }
     if(rt->rid!=NULL&&
         rt->maxn < rt->rid->maxn)
             rt->maxn = rt->rid->maxn;
 }
 int dep[N],fa[N][logN],ln;
 bool is_v[N];
 struct Myqu{
     int f,e;
     int Q[N*];
     void push(int k){
         e++;
         Q[e]=k;
     }
     int front(){
         f++;
         return Q[f];
     }
     bool empty(){
         if(e==f)return true;
         return false;
     }
 }qu;
 void bfs(int k){
     qu.push(k);
     is_v[k]=;
     while(!qu.empty()){
         int f=qu.front();
         for(int i=fl[f];i!=-;i=rs[i].next){
             if(!is_v[rs[i].t]){
                 qu.push(rs[i].t);
                 is_v[rs[i].t]=;
                 fa[rs[i].t][]=f;
                 dep[rs[i].t]=dep[f]+;
                 for(int j=;j<=ln;j++) fa[rs[i].t][j]=fa[fa[rs[i].t][j-]][j-];
             }
         }
     }
 }
 int lca(int a,int b){//cout<<a<<SP<<b<<endl;
     if(dep[a]>dep[b])swap(a,b);
     for(int i=ln;i>=;i--)
         if(dep[fa[b][i]]>=dep[a]){
             b=fa[b][i];
             //cout<<" "<<b<<" Dep"<<dep[b]<<endl;
         }
     if(a==b) return b;
     for(int i=ln;i>=;i--)
         if(fa[a][i]!=fa[b][i]){
             a=fa[a][i],b=fa[b][i];
         }
     return fa[a][];
 }
 XDS* merge(int l,int r,XDS *&a,XDS *&b){
     if(a==NULL)return b;
     if(b==NULL)return a;
     if(l==r){
         a->maxn =a->maxn+b->maxn;
         delete b;
         b=NULL;
         return a;
     }
     int mid=(l+r)>>;//puts("midgot");
     a->lid=merge(l,mid,a->lid,b->lid);//puts("Lid merge end");
     a->rid=merge(mid+,r,a->rid,b->rid);
     if(a->lid!=NULL){
         a->maxn  = a->lid->maxn;
     }
     if(a->rid!=NULL&&
         a->rid->maxn > a->maxn)
             a->maxn =a->rid->maxn;
     return a;
 }
 int ffind(XDS *rt,int l,int r){
     int mid=(l+r)>>;
     if(rt==NULL)return -;
     if(l==r)return l;
     if(rt->lid==NULL&&rt->rid==NULL)return -;
     if(rt->lid==NULL)return ffind(rt->rid,mid+,r);
     if(rt->rid==NULL)return ffind(rt->lid,l,mid);
     if(rt->lid->maxn>=rt->rid->maxn){
         return ffind(rt->lid,l,mid);
     }
     else return ffind(rt->rid,mid+,r);
 }
 void getans(int k){
     is_v[k]=;
     for(int i=fl[k];i!=-;i=rs[i].next){
         if(is_v[rs[i].t]){
             getans(rs[i].t);
             root[k]=merge(,len,root[k],root[rs[i].t]);
         }
     }
     int q=ffind(root[k],,len);
     if(q==-)dep[k]=;
     else dep[k]=val[q-];
 }
 int du[N];
 int main(){
     int a,b,c,ro;
     memset(fl  ,-,sizeof fl);
     scanf("%d%d",&n,&m);
     ln=log2(n)+;
     for(int i=;i<n;i++){
         scanf("%d%d",&a,&b);
         add(a,b);
         add(b,a);
     }
     for(int i=;i<=m;i++){
         scanf("%d%d%d",&a,&b,&c);
         q[i].x=a ,q[i].y=b ,q[i].z=val[i-]=c;
         du[a]++,du[b]++;
     }
     int maxn=-;
     for(int i=;i<=n;i++){
         if(du[i]>maxn){
             ro=i;
             maxn=du[i];
         }
     }
     sort(val+,val+m);
     len=unique(val,val+m)-val;
     dep[ro]=;
     bfs(ro);
     for(int i=;i<=m;i++){
         int Lca=lca(q[i].x,q[i].y),val=fvind(q[i].z);
         add(root[Lca],       val,-,,len);
         add(root[fa[Lca][]],val,-,,len);
         add(root[q[i].x]    ,val, ,,len);
         add(root[q[i].y]    ,val, ,,len);
     }
     getans(ro);
     for(int i=;i<=n;i++){
         printf("%d\n",dep[i]);
     }
     return ;
 }

Total Code