BZOJ3325 [Scoi2013]密码【manacher】

题目

Fish是一条生活在海里的鱼。有一天他很无聊，就到处去寻宝。他找到了位于海底深处的宫殿，但是一扇带有密码锁的大门却阻止了他的前进。通过翻阅古籍，Fish 得知了这个密码的相关信息：

该密码的长度为N。
密码仅含小写字母。
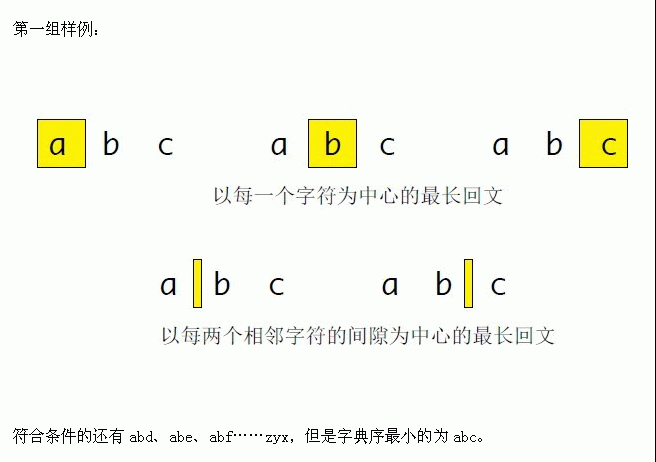
以每一个字符为中心的最长回文串长度。
以每两个相邻字符的间隙为中心的最长回文串长度。

很快Fish 发现可能有无数种满足条件的密码。经过分析，他觉得这些密码中字典序最小的一个最有可能是答案，你能帮他找到这个密码么？

注意：对于两个串A和B，如果它们的前i个字符都相同，而A的第i+1个字符比B的第i+1个字符小，那么认为是则称密码A 的字典序小于密码B 的字典序，例如字符串abc 字典序小于字符串acb。如果密码A的字典序比其他所有满足条件的密码的字典序都小，则密码A是这些密码中字典序最小的一个。

输入格式

输入由三行组成。

第一行仅含一个整数N，表示密码的长度。

第二行包含N 个整数，表示以每个字符为中心的最长回文串长度。

第三行包含N - 1 个整数，表示每两个相邻字符的间隙为中心的最长回文串长度。

对于20% 的数据，1 <= n <= 100。

另有30% 的数据，1 <= n <= 1000。

最后50% 的数据，1 <= n <= 10^5。

输出格式

输出仅一行。输出满足条件的最小字典序密码。古籍中的信息是一定正确的，故一定存在满足条件的密码。

输入样例

1 1 1

0 0

输出样例

abc

提示

题解

根据贪心的思想，我们当然是每个位置在满足条件下尽量选小的

我们从左开始选字符

每到达一个位置，由于其之前的位置已经确定，由回文串我们可以确定后面对应的位置

又由于每个最长回文串的端点处的下一位一定是不同的，可以用一个数组记录每个位置不能取的值

#include<iostream>

#include<cstdio>

#include<cmath>

#include<cstring>

#include<algorithm>

#define LL long long int

#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)

#define REP(i,n) for (int i = 1; i <= (n); i++)

#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");

using namespace std;

const int maxn = 100005,maxm = 100005,INF = 1000000000;

inline int read(){

	int out = 0,flag = 1; char c = getchar();

	while (c < 48 || c > 57){if (c == '-') flag = -1; c = getchar();}

	while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}

	return out * flag;

}

int ans[maxn],n;

int R[maxn],r[maxn];

int isn[maxn][26];

int main(){

	memset(ans,-1,sizeof(ans));

	n = read();

	for (int i = 1; i <= n; i++) R[i] = (read() >> 1) + 1;

	for (int i = 1; i < n; i++) r[i] = read() >> 1;

	int mr = 1; ans[1] = 0;

	for (int i = 1; i <= n; i++){

		if (ans[i] == -1) for (int j = 0; j < 26; j++) if (!isn[i][j]){

			ans[i] = j;

			mr = i;

			break;

		}

		while (mr < i + R[i] - 1) ++mr,ans[mr] = ans[2 * i - mr];

		while (i < n && mr < i + r[i]) ++mr,ans[mr] = ans[2 * i - mr + 1];

		if (i + R[i] <= n && i - R[i] > 0)

			isn[i + R[i]][ans[i - R[i]]] = true;

		if (i < n && i + r[i] + 1 <= n && i - r[i] > 0)

			isn[i + r[i] + 1][ans[i - r[i]]] = true;

	}

	for (int i = 1; i <= n; i++) putchar(ans[i] + 'a');

	return 0;

}