[刷题] 343 Integer Break

要求

• 给定一个正数n，可将其分割成多个数字的和，求让这些数字乘积最大的分割方法（至少分成两个数）

示例

• n=2，返回1（2=1+1）
• n=10，返回36（10=3+3+4）

实现

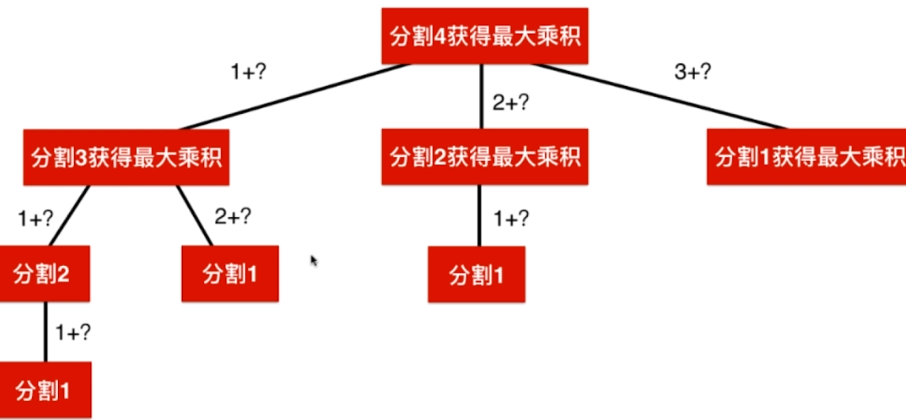
• 回溯遍历（n^2，超时）

 1 class Solution {
 2 private:
 3     int max3( int a , int b , int c ){
 4         return max( a , max(b,c) );
 5     }
 6
 7     // 将n进行分割（至少两部分）可获得的最大乘积
 8     int breakInteger(int n){
 9
10         if( n == 1 )
11             return 1;
12
13         int res = -1;
14         for( int i = 1 ; i <= n-1 ; i ++ )
15             // i + (n-i)
16             res = max3( res, i * (n-i) , i * breakInteger(n-i) );
17
18         return res;
19     }
20
21 public:
22     int integerBreak(int n) {
23         return breakInteger(n);
24     }
25 };

• 记忆化搜索
  • 21：不要写成 res=max(res,i*breakInteger(n-i))，breakInteger(n-i) 将 n-i 至少分成两部分，不分割的话就是 i*(n-i)
  • 自定义传入3个数求最大值的函数

 1 class Solution {
 2 private:
 3     vector<int> memo;
 4
 5     int max3( int a , int b , int c ){
 6         return max( a , max(b,c) );
 7     }
 8
 9     // 将n进行分割（至少两部分）可获得的最大乘积
10     int breakInteger(int n){
11
12         if( n == 1 )
13             return 1;
14
15         if( memo[n] != -1)
16             return memo[n];
17
18         int res = -1;
19         for( int i = 1 ; i <= n-1 ; i ++ )
20             // i + (n-i)
21             res = max3( res, i * (n-i) , i * breakInteger(n-i) );
22         memo[n] = res;
23         return res;
24     }
25
26 public:
27     int integerBreak(int n) {
28         memo = vector<int>(n+1,-1);
29         return breakInteger(n);
30     }
31 };

• 动态规划
  • 重叠子问题：有相同的子问题，可采用记忆化搜索进行优化
  • 最优子结构：通过求子问题的最优解，可以获得原问题的最优解
  • 如：想获得分割n的最大乘积，需要知道分割n-1，n-2...，1等的最大乘积
  • 满足重叠子问题 + 最优子结构的递归问题，可以用记忆化搜索/动态规划求解

 1 class Solution {
 2 private:
 3     int max3( int a , int b , int c ){
 4         return max( a , max(b,c) );
 5     }
 6
 7 public:
 8     int integerBreak(int n) {
 9         assert( n >= 2 );
10
11         // memo[i]表示至少将数字i分割（至少两部分）后得到的最大乘积
12         vector<int> memo(n+1,-1);
13
14         memo[1] = 1;
15         for( int i = 2 ; i <= n ; i ++ )
16             // 求解memo[j]
17             for( int j = 1 ; j <= i-1 ; j ++ )
18                 // j + (i-j)
19                 memo[i] = max3(j*(i-j) , j*memo[i-j] , memo[i] );
20
21         return memo[n];
22     }
23 };

相关

• 279 Perfect Squares
• 91 Decode Ways
• 62 Unique Paths
• 63 Unique Paths II