go实现堆排序、快速排序、桶排序算法

一. 堆排序

　　堆排序是利用堆这种数据结构而设计的一种排序算法。以大堆为例利用堆顶记录的是最大关键字这一特性，每一轮取堆顶元素放入有序区，就类似选择排序每一轮选择一个最大值放入有序区，可以把堆排序看成是选择排序的改进。它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

堆

　　堆是一棵完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

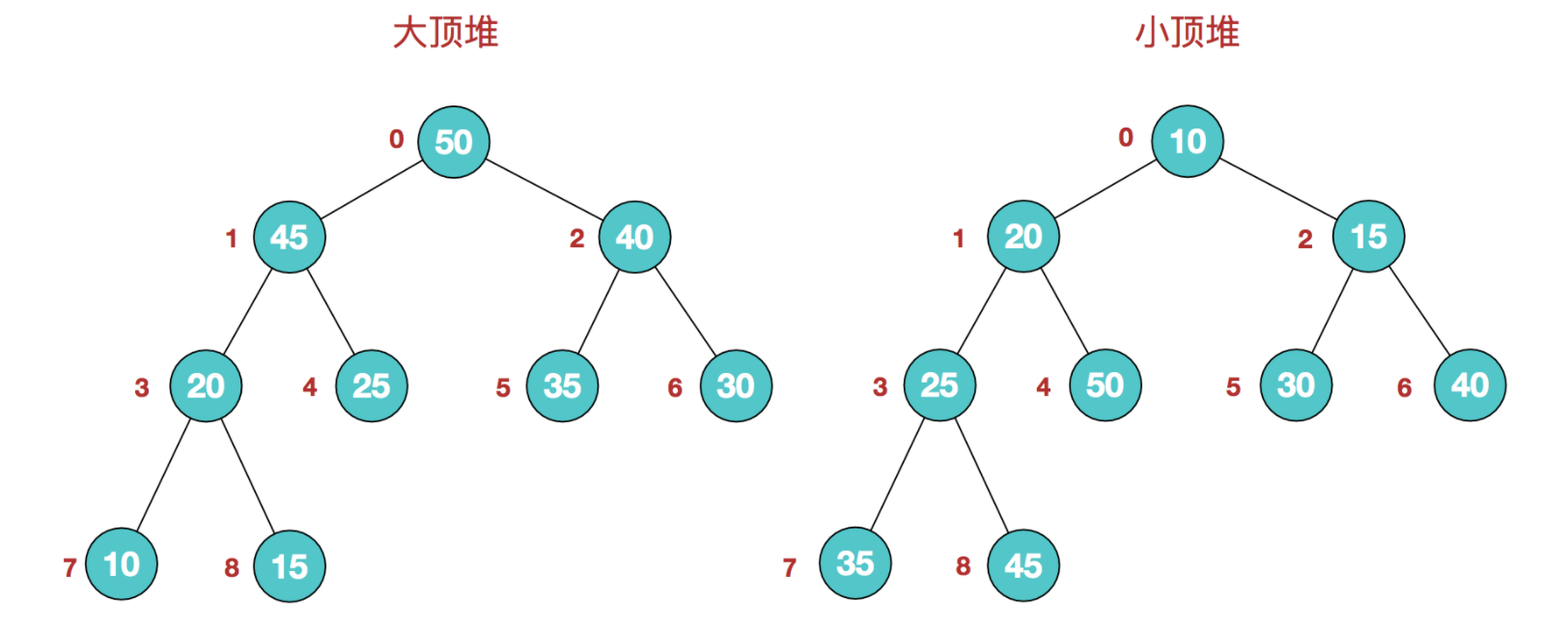
对堆中的结点按层进行编号，将这种逻辑结构映射到数组中：

由于它是一颗完全二叉树，所以满足序号

leftchild = parent * 2 + 1;

rightchild = parent * 2 + 2;

这样的特性，利用这一特性，每次将parent与child进行比较然后向下调整元素的位置。

实现堆排序

1. 将初始待排序关键字序列(R0,R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；初始堆满足大顶堆性质，但是元素无序。
2. 依次将将堆顶元素R[0]与最后一个元素R[n]交换，此时得到新的无序区(R0,R1,R2,......Rn-1)和新的有序区(Rn)；
3. 交换后进行向下调整无序区，使其满足大顶堆性质。
4. 循环执行 2.3 步骤 直到遍历完数组。

 1 func HeapSort(arr []int)  {
 2     arrLen := len(arr)
 3     for i := (arrLen-2)/2; i >= 0; i-- {
 4         arrJustDown(arr, i, arrLen)
 5     }
 6     end := arrLen - 1
 7     for end != 0 {
 8         arr[0], arr[end] = arr[end], arr[0]
 9         arrJustDown(arr, 0, end)
10         end--
11     }
12     fmt.Println(arr)
13 }
14 func arrJustDown(arr []int, root, n int) {
15     parent := root
16     child := parent * 2 + 1
17     for child < n {
18         if child + 1 < n && arr[child + 1] > arr[child] {
19             child++
20         }
21         if arr[child] > arr[parent] {
22             arr[child], arr[parent] = arr[parent], arr[child]
23             parent = child
24             child = parent * 2 + 1
25         } else {
26             break
27         }
28     }
29 }

　　建堆和每次向下调整的时间复杂度都是long2N ,所以整个数组处理完后，需要执行Nlong2N遍，调整过程中，最后一个元素和堆顶元素交换后需要向下调整，所以不保证相同大小元素的位置不变，它是不稳定排序。

二. 快速排序

排序思想

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

排序实现

步骤为：（1）从数列中挑出一个元素，称为 "基准"（pivot）；

　　       （2）重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。

　　　　（3）递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

　　当我们每次划分的时候选择的基准数接近于整组数据的最大值或者最小值时，快速排序就会发生最坏的情况，但是每次选择的基准数都接近于最大数或者最小数的概率随着排序元素的增多就会越来越小，我们完全可以忽略这种情况。但是在数组有序的情况下，它也会发生最坏的情况，为了避免这种情况，我们在选择基准数的时候可以采用三数取中法来选择基准数。 
三数取中法： 选择这组数据的第一个元素、中间的元素、最后一个元素，这三个元素里面值居中的元素作为基准数。

 1 func QuickSort(arr []int)  {
 2     arrLen := len(arr)
 3     quickSort(arr, 0, arrLen - 1)
 4     fmt.Println(arr)
 5 }
 6 func quickSort(arr []int, left, right int)  {
 7     if left < right {
 8         mid := partSort(arr, left, right)
 9         quickSort(arr, left, mid - 1)
10         quickSort(arr, mid + 1, right)
11     }
12 }
13 func partSort(arr []int, left, right int) (ret int) {
14     key := arr[right]
15     for left < right {
16         for left < right && arr[left] <= key {
17             left++
18         }
19         arr[right] = arr[left]
20         for left < right && arr[right] >= key {
21             right--
22         }
23         arr[left] = arr[right]
24     }
25     arr[left] = key
26     ret = left
27     return
28 }

快速排序是一种快速的分而治之的算法，其平均运行时间为O(N*1ogN) 。它的速度主要归功于一个非长紧凑的并且高度优化的内部循环。但是他也是一种不稳定的排序，当基准数选择的不合理的时候他的效率又会编程O(N*N)。快速排序的最好情况： 快速排序的最好情况是每次都划分后左右子序列的大小都相等，其运行的时间就为O(N*1ogN)。快速排序的最坏情况： 快速排序的最坏的情况就是当分组重复生成一个空序列的时候，这时候其运行时间就变为O(N*N)快速排序的平均情况： 平均情况下是O(N*logN)。

三. 桶排序

介绍

　　基本原理是将数组分到有限数量的桶里。每个桶再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序），最后依次把各个桶中的记录列出来记得到有序序列。当要被排序的数组内的数值是均匀分配的时候，桶排序使用线性时间（Θ(n)）。但桶排序并不是比较排序，他不受到O(n log n)下限的影响。

排序思想

　　桶排序的思想近乎彻底的分治思想。假设待排序的一组数均匀独立的分布在一个范围中，并将这一范围划分成几个子范围（桶）。然后基于某种映射函数f ，将待排序列的关键字 k 映射到第i个桶中 (即桶数组B 的下标i) ，那么该关键字k 就作为 B[i]中的元素 (每个桶B[i]都是一组大小为N/M 的序列 )。接着将各个桶中的数据有序的合并起来 : 对每个桶B[i] 中的所有元素进行比较排序 (可以使用快排)。然后依次枚举输出 B[0]….B[M] 中的全部内容即是一个有序序列。

　　为了使桶排序更加高效，我们需要做到这两点：

1. 在额外空间充足的情况下，尽量增大桶的数量
2. 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

实现逻辑

• 设置一个定量的数组当作空桶子。
• 寻访序列，并且把项目一个一个放到对应的桶子去。
• 对每个不是空的桶子进行排序。
• 从不是空的桶子里把项目再放回原来的序列中。

动图演示排序过程：

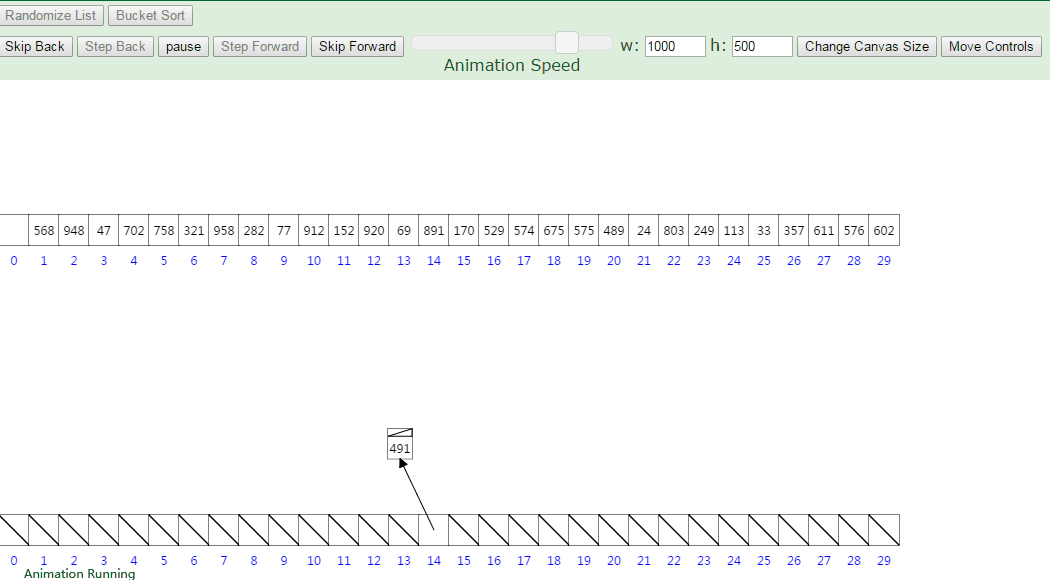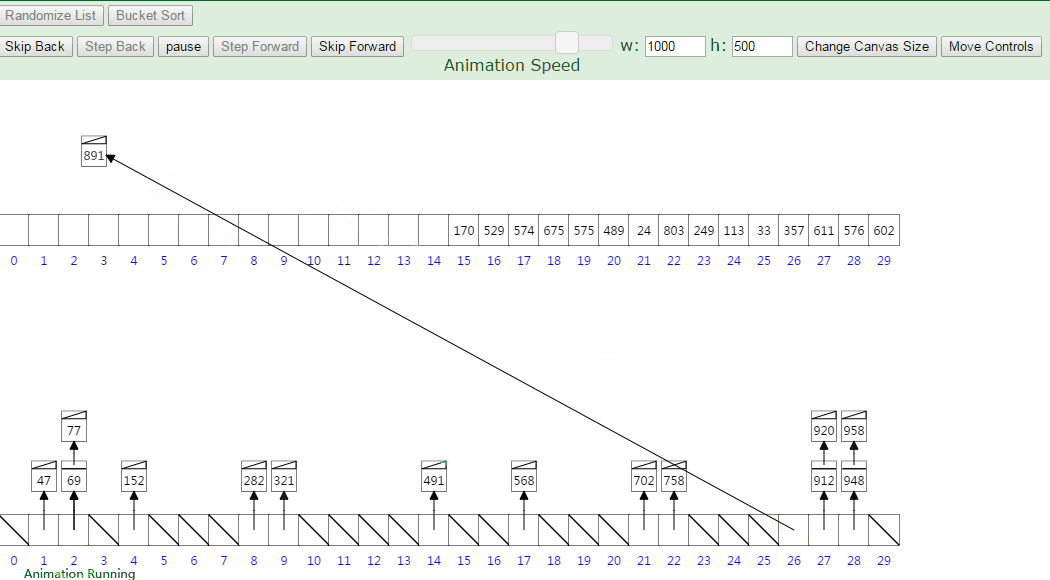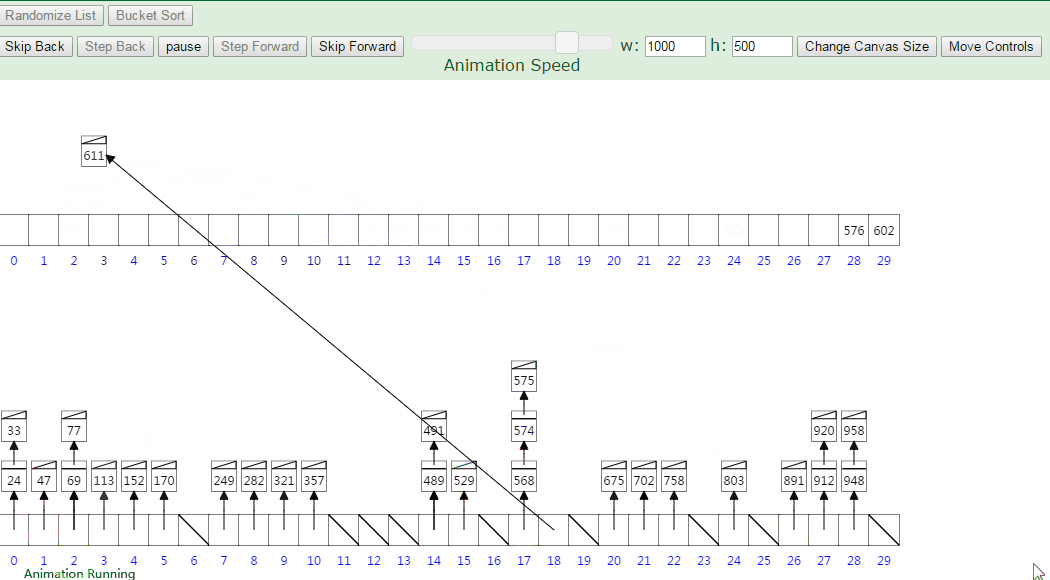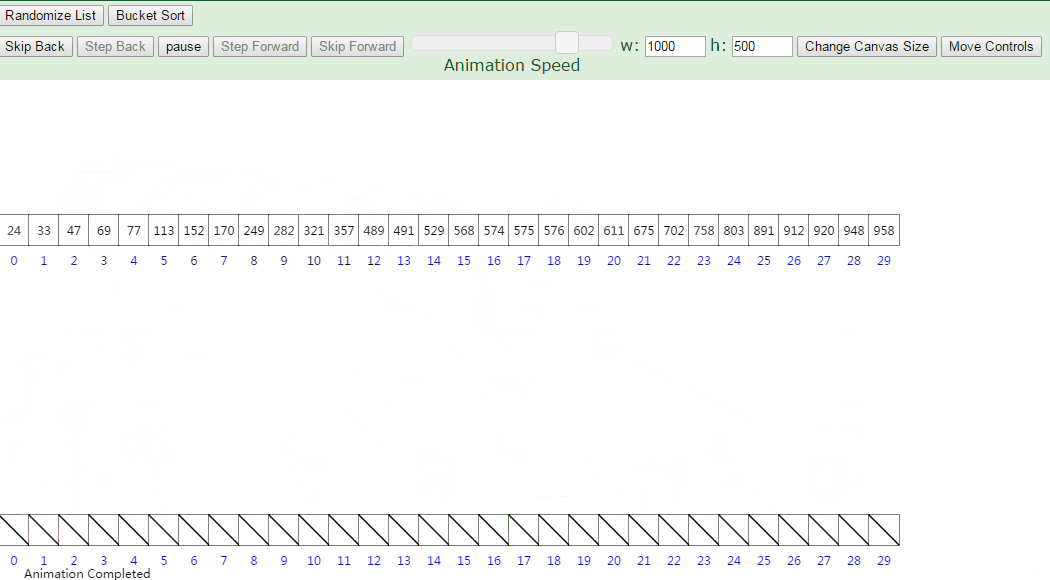
设有数组 array = [63, 157, 189, 51, 101, 47, 141, 121, 157, 156, 194, 117, 98, 139, 67, 133, 181, 13, 28, 109]

对其进行桶排序：

复杂度

• 平均时间复杂度：O(n + k)
• 最佳时间复杂度：O(n + k)
• 最差时间复杂度：O(n ^ 2)
• 空间复杂度：O(n * k)
• 稳定性：稳定

　　桶排序最好情况下使用线性时间O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

go代码实现

 1 func bin_sort(li []int, bin_num int) {
 2     min_num, max_num := li[0], li[0]
 3     for i := 0; i < len(li); i++ {
 4         if min_num > li[i] {
 5             min_num = li[i]
 6         }
 7         if max_num < li[i] {
 8             max_num = li[i]
 9         }
10     }
11     bin := make([][]int, bin_num)
12     for j := 0; j < len(li); j++ {
13         n := (li[j] - min_num) / ((max_num - min_num + 1) / bin_num)
14         bin[n] = append(bin[n], li[j])
15         k := len(bin[n]) - 2
16         for k >= 0 && li[j] < bin[n][k] {
17             bin[n][k+1] = bin[n][k]
18             k--
19         }
20         bin[n][k+1] = li[j]
21     }
22     o := 0
23     for p, q := range bin {
24         for t := 0; t < len(q); t++ {
25             li[o] = bin[p][t]
26             o++
27         }
28     }
29 }

　　桶排序是计数排序的变种，它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。把计数排序中相邻的m个”小桶”放到一个”大桶”中，在分完桶后，对每个桶进行排序（一般用快排），然后合并成最后的结果。

　　算法思想和散列中的开散列法差不多，当冲突时放入同一个桶中；可应用于数据量分布比较均匀，或比较侧重于区间数量时。

　　桶排序最关键的建桶，如果桶设计得不好的话桶排序是几乎没有作用的。通常情况下，上下界有两种取法，第一种是取一个10n或者是2n的数，方便实现。另一种是取数列的最大值和最小值然后均分作桶。