学军中学csp-noip2020模拟5

Problem List（其实这几场全是附中出的）

这场比赛的题目相当有价值，特别是前两题，相当的巧妙。

A.路径二进制

数据范围这么小，当然是搜索。

\(30pts:\)大力搜索出奇迹，最后统计答案的时候拿一个桶存一下已经统计了哪些数，由于\(d<=20\)，所以\(result<=2^20\)，所以还是存的下的。

\(60pts:\)我们发现重复状态其实非常之多，我们加上一个记忆化进行剪枝：\(vis[i][t][S]\)表示\(i\)号点、时间是\(t\)、当前数是\(S\)是否已经访问过，如果已经访问过那就可以回溯了。时间复杂度和空间复杂度都是\(O(nd2^d)\)的，时间上可以过满数据，但是空间会被卡。

\(100pts:\)相当巧妙的方法来优化空间：我们在搜索时进行折半，只从一开始搜索长度为\(\frac{1}{2}d\)的链并用状压存下是否可达存下来，然后分别在每个点往外搜索长度为\(\frac{1}{2}d\)的链并状压存下，最后遍历每个点暴力合并前后两段就可以了。空间复杂度是\(n^22^{\frac{1}{2}d}+2^d\)的，时间是\(n^22^d\)的。

B.停车场

\(20pts:\)悬线法可以解决静态的平面最大全0矩阵问题。当然也可以用\(DP\)解决：设\(f_{i,j}\)为在结点\((i,j)\)向左上能延伸的最大方形的边长，\(h_{i,j}\)为向上能有多少个空位，\(r_{i,j}\)是向左的空位，于是得到\(f_{i,j}=min\{r_{i,j},h_{i,j},f_{i-1,j-1}+1\$。复杂度\)O(n^2m)$。

\(70pts:\)你会发现没有这一档部分分，这个是我考场上乱搞搞出来的分数。你会发现一个神奇的性质：

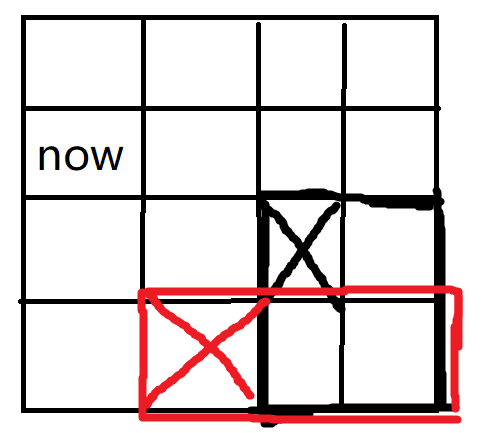
假设我们要在\(now\)这个点放一辆车，那么它只会对它右下角的点的\(DP\)值产生影响，并且下面这种已经放过车的右下方的位置的\(DP\)值也没有影响，所以我们要更新的点的数量就比较有限了。关于如何遍历这个奇形怪状的东西，我们只需要一行一行枚举，存一下当前遇到的最左边的车的横坐标，以后便利的横坐标都要小于这个值就行了）。另外我们要动态查询\(f\)的最大值，这个东西用一棵权值线段树当成平衡树跑就可以实现\(log\)级别，所以总的时间复杂度最劣是\(O(n^2dlogn)\)的，但是只要随机它能飞起来。

\(100pts:\)简直精妙到不得了的，时间复杂度应该是最劣\(n^2logn+mn\)的。答案显然是递减的，并且答案的值域就只有\([1,2000]\)，还是满足决策单调性的！这就使人浮想联翩了。由于加上一辆车可能会破坏很多答案，破坏性质不优美，即使用平衡树维护啥的都很吃力，所以我们反过来想：我们移走一辆车，看看包括它的矩形最大是多少的，这个时候两个答案取\(max\)是满足交换律的，相当优美。

但是光光这样还是相当困难。我们再加上一个小小的转换：记录上一次的答案是\(lastans\)，那么我这次就依次验证有没有矩形包含这个新空格且大小为\(lastans+1\)、\(lastans+2\)······直到不合法为止。这个可以用平衡树来解决：设\(r1_{i,j}\)、\(r2\)、\(r3\)、\(r4\)分别是它向四个方向能延伸多少，那么我在指定空格的那个纵列上依次扫下来，看看这个高度为\(lastans+1\)的窗口内的向左、向右的最小值加起来是否能够大于等于\(lastans+1\)。显然一个空格只会影响它所在的那一横一竖的\(r\)，暴力修改即可。

它的时间复杂度显然是均摊的，最劣是\(n^2logn+mn\)，据说用并查集可以优化到\(n^2\alpha\)的。

这启发我们在答案值域很小、满足单调性和决策单调性的时候可以使用反过来的、判定性的方法解决问题。