Deep Upsupervised Cardinality Estimation

本篇博客是对Deep Upsupervised Cardinality Estimation的解读，原文连接为：https://dl.acm.org/doi/pdf/10.14778/3368289.3368294
本文介绍了如何使用深度自回归模型（如：MADE、transformer）来进行基数估计的任务（利用模型训练拟合数据分布）
特点：
- 使用autoregressive model，无监督学习
- 没有做任何独立性假设
- 支持范围查询

选择度（基数）估计问题定义

selectivity——选择度。本文针对的是给定谓词，估计其可以估计数据表中满足该谓词的元组的比例，有如下定义：$$sel(\theta):=|{\ x \in T :\theta (x)=1}|/|T|$$

其中分母T就是表的总行数，分子是满足选择谓词的行数。

选择度和数据联合分布的关系

文中给出联合分布(joint distribution)的定义：

\[P(a_1,a_2,...,a_n):=f(a_1,a_2,...,a_n)/T
\]

其中分母T仍表示表行数，f为满足a1，a2...an条件的行数。因此实际上联合分布和选择度有着十分紧密的联系（基本一致）。同时联合分布还可以通过因式分解（factorization）写成：

\[P(A_1,A_2,...A_n):=\hat{P}(A_1) \hat{P}(A_2|A_1)...\hat{P}(A_n|A_1,A_2,...A_{n-1})
\]

该式没有进行任何独立性假设，而且保留了属性之间的相互联系，因此想获得相对准确的选择度，实际上就是要构建能计算上式的模型。

深度自回归模型如何计算joint distribution

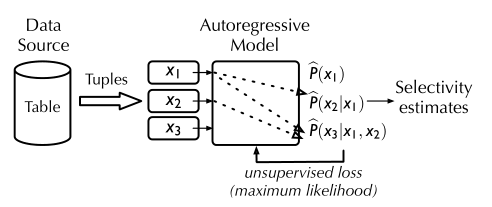
作者选用Autoregressive Model进行对数据联合分布的拟合。以某一列为例。对于一列数据的分布，模型的input为前几列值的组合（因为是条件概率），输出的是在前几列的条件下，改列的分布概率。例如一张表travel_checkins含有三个属性：city、year、stars。给定一行作为输入：<Portland;2017;10>:
\[0\rightarrow M(city)
\]

\[E_{city}(Portland)\rightarrow M(year)
\]

\[(E_{city}(Portland)\oplus E_{year}(2017)) \rightarrow M_{star}
\]

上式三个输出依次是条件概率：$$\hat{P}(city),\hat{P}(year|city),\hat{P}(star|city,year)$$

下图简略展示了模型的工作流

编码解码策略

在训练模型时，我们必须将数据表中的各个元素编码成机器能够看懂的语言，模型输出时我们要将编码进行解码得到各种概率，下面介绍作者提出的编码解码策略。

small-domain：
- encodding：one-hot
- decoding：一个全连接层FC（F，|Ai|），其中F为隐藏层大小，|Ai|第i列的值域大小。输出一个长度|Ai|的向量，每个元素表示位于该值的概率。
large-domain：
- encodding：Embedding，通过词嵌入将各值映射为一个固定长度h的向量
- decoding：Embedding reuse。当属性值域太大时，向上面一样使用一个全连接层产生一个非常长的向量，这在空间上和计算复杂度上都十分低效。在这里作者提出Embedding reuse，同样使用一个全连接层FC（F,h），其中F还是隐藏层的大小，h为Embedding规定的向量长度，这样神经网络就会生成一个长度为h的向量H，接着通过计算$HE_i^T$并对其进行标准化处理，我们就能得到一个代表选择度的度量值。

具体执行

本文提供的方法支持点查询和范围查询，一般来说$sel=P(X_1\in R_1,X_2\in R_2,...X_n\in R_3)$

点查询，即等值查询,将上式转换为：$sel=P(X_1=x_1,X_2=x_2,...X_n=x_3)$
范围查询：对于范围查询，本文采用渐进采样的方法对数据表进行采样进行概率的估计
wildcard-skipping：这里提到的通配符不是指like查询，而是指age = any，也就是age可以为任何值，即范围查询age = [0, Di]。所以这里提到的通配符是为了满足有些条件没有filter的处理。

为了达到这个目的，作者设计了特殊的token，Xi = MASKi，如age这一列的token为MASK_age。训练的时候，会把每一列用这个token替换掉，进行训练（这样就需要训练n次？n为列的个数，相当于数据被复制了n份，每一份把一列的值替换为token）。

实际操作的时候，会随机sample一个tuple，age对应的值换成MASK_age，表明age取所有值，其他值的条件概率就是当age取所有值的情况下，其条件概率为多少，作为label。至于sample多少条数据，这个要看具体效果了。

另外要根据实际的query确定哪些列需要有这个通配符。再举个具体的例子，一个表有三列a b c，查询为a=1，那么模型训练的时候必须要有b=MASK_b，c=MASK_c，查询的输入为a=1, b=MASK_b，c=MASK_c。再如a<10，一种方法是sampling，还有一种方法是模型训练的时候要有a=MASK_a, 这样查询的时候输入是a=MASK_a, b=MASK_b，c=MASK_c，a的输出会得到所有的值，再把<10对应的值的概率加起来。

所以，这个通配符是非常有用的，因为在真实查询中，不可能保证所有列上都有条件，那么没有条件的列就用通配符替代。当然也可以用sampling的方式，但是通配符的查询效率更高。

属性的顺序

从上面的分析中可以看到每列实际上是有顺序的，比如模型的输入是列a b c，输出是条件概率，既然是条件概率，那么b的概率是给定a得到，c的概率是给定a和b得到。所以这个顺序要提前定好，如果查询是b=1 a=2，需要把顺序调整成a=2 b=1输入到模型。

均匀采样和渐进采样

两种sampling策略是为了解决范围查询的选择度估计问题。

假定一个范围查询域$R=R_1\times R_2 \times ... \times R_n$,如果用等值的方法处理这种问题，在某种比较坏的情况下，查询域可能会非常大（比如可能为$|A_1|\times |A_2| ... |A_n|$）,此时非常耗费时间和空间。为了解决这种问题，本文尝试了两种解决方案：

uniformly sampling
- 从R（查询域）中均匀随机抽样出$x^{(i)}$,接着将该$x^{(i)}$输入模型，计算出该样本在数据表中的概率：$\hat{p_i}=\hat{P}(x^{(i)})$，基于朴素蒙特卡洛，对于S个样本，我们可以将$\frac{|R|}{S}\sum_{i=1}^{S}\hat{p_i}$作为期望密度的无偏估计。简单来说，该方案是将点随机扔到目标区域R中，以探测其平均密度。
- 均匀采样的缺点：考虑这样一个情况，数据表T有n个属性列，但每一列的数据都非常倾斜，有99%的数据只集中在前1%的值域中，剩下1%的数据分散到后99%的值域内。在这种情况下，如果我们想进行值域前50%的范围查询。通过随机抽样我们大概率只能抽到1%-50%内的数据，计算出的结果会严重失真。如果要保持准确性，我们必须抽$1/(0.01/0.5)^n=1/0.02^n$个样本才能都取到数据高密度区域。真实的数据集中，这样倾斜的数据常有出现，当均匀抽样遇到这样的数据会很快崩溃，产生非常大的误差如下图左，这里我们使用下文提出的渐进采样来决绝该问题。
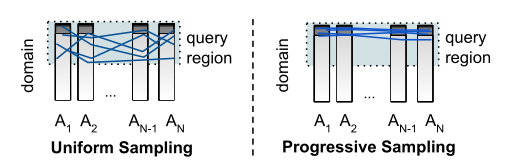
progressive sampling
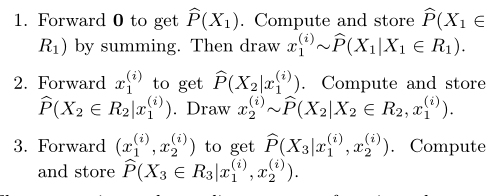
- 渐进采样。在均匀采样中，我们是随机的在查询域中选择了一组样本。但实际上，我们可以更有选择性的挑选样本。具体来说我们可以利用模型一边生成各个属性的概率分布，一边按照生成的概率分布进行采样，因为是逐步进行采样的所以叫渐进采样。通过渐进采样，我们能很容易的采样到高数据密度的区域，如上图右。步骤如下：

(*^▽^*)

(*^▽^*)

(*^▽^*)

(*^▽^*)

(*^▽^*)

笔者解读不易，若是有所帮助，给笔者点个赞吧(*^▽^*)

欢迎来与笔者交流相关问题！