「CF559E」 Gerald and Path

「CF559E」 Gerald and Path

为啥我现在做啥题都在想网络流啊

考虑 \(\texttt{DP}\)。

容易想到状态应该包含当前枚举了前 \(i\) 条线段，且第 \(i\) 条线段的方向。

然后你会发现计算贡献并不方便，因为你新加一条线段并不能非常方便的算出它对答案的贡献。

于是我们考虑先对线段端点排序，再考虑储存当前最靠右的线段端点位置，这样新加一条线段的贡献可能会更好计算。

然后你发现还是有特殊情况，有可能你新加的这一条线段不仅两端有贡献，中间也有贡献，你觉得很烦。

图大概长这样

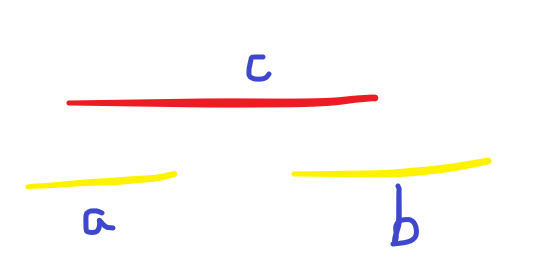
然后你发现事实上 \(b\) 线段和 \(c\) 线段可以合并看成实际上只有一条线段，即端点在 \(c\) 线段右边的线段若被完全包含就不管，能合并就合并掉了，问题就转变成只有两端有贡献了。

所以状态为 \(f_{i,j,0/1}\) 表示前 \(i\) 条线段，最右端点为 \(j\)，第 \(i\) 条线段的方向为左/右的答案。

转移即可，注意上面说到的类似于合并线段的问题即可。时间复杂度为 \(O(n^3)\)。

/*---Author:HenryHuang---*/
/*---Never Settle---*/
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e2+5;
pair<int,int> seg[maxn];
int f[maxn][maxn][2];
int ans;
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	int n;cin>>n;
	for(int i=1;i<=n;++i) cin>>seg[i].first>>seg[i].second;
	sort(seg+1,seg+n+1);seg[0].first=-(1<<30);
	for(int i=0;i<=n;++i){
		for(int j=0;j<=i;++j){
			for(int k=0;k<2;++k){
				ans=max(ans,f[i][j][k]);
				int nr=seg[j].first+seg[j].second*k,mx=-(1<<30),x=0,y=0;
				for(int l=i+1;l<=n;++l){
					for(int m=0;m<2;++m){
						int tr=seg[l].first+seg[l].second*m;
						if(tr>mx) mx=tr,x=l,y=m;
						f[l][x][y]=max(f[l][x][y],f[i][j][k]+mx-tr+min(seg[l].second,tr-nr));
					}
				}
			}
		}
	}
	cout<<ans<<'\n';
	return 0;
}