Solution -「洛谷 P5236」「模板」静态仙人掌

\(\mathcal{Description}\)

  Link.

  给定一个 \(n\) 个点 \(m\) 条边的仙人掌，\(q\) 组询问两点最短路。

  \(n,q\le10^4\)，\(m\le2\times10^4\)。

\(\mathcal{Solution}\)

  提出一个环来考虑，从环上一点 \(u\) 到 \(v\)，无非两条路径。可以按顺序处理一个前缀和。如图：

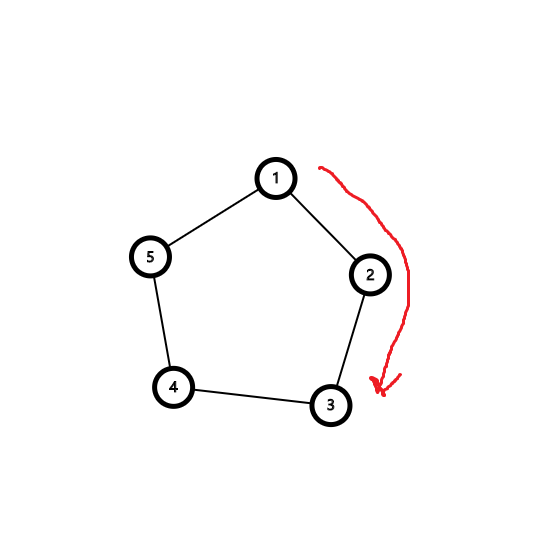
  令 \(sum_2\) 为结点 \(1\) 到 \(2\) 的顺时针距离，\(sum_3\) 为结点 \(1\) 到 \(3\) 的顺时针距离……特别地，\(sum_1\) 记录整个环的大小。那么环上 \(u\) 和 \(v\) 的最短距离就是 \(\min\{|sum_u-sum_v|,sum_1-|sum_u-sum_v|\}\)。这样就能 \(\mathcal O(1)\) 求到了。

  接下来建圆方树（很多题解说建树的细节与普通图不一样，其实正常建也没有任何问题 qwq），发现一个圆点走进方点（点双），在走到父亲圆点的最短距离可以在 \(\text{Tarjan}\) 算法中预处理出来。考虑圆方树上的边权：圆点到父亲方点的边权为上述最短距离，否则为 \(0\)。对于询问 \((u,v)\)，找到其 \(\text{LCA}\)（设为 \(w\)），分 \(w\) 的情况讨论：

• \(w\) 是圆点，那么 \(\text{LCA}\) 时求出的树上距离就是答案。
• \(w\) 是方点，此时树上距离实际上是 \(u\) 和 \(v\) 走到 \(w\) 的父亲圆点的距离之和，明显时错误的——\(u\) 和 \(v\) 走进同一个点双后，需要求一次最短距离而非直接在父亲会和。所以可以倍增求到 \(u\) 走进点双的第一个点（即方点向 \(u\) 点方向的儿子圆点）\(u'\)，同理求出 \(v'\)，利用处理的前缀和求到 \(u'\) 到 \(v'\) 的最短距离。那么答案就是 \(\operatorname{dist}(u,u')+\operatorname{dist}(u',v')+\operatorname{dist}(v',v)\)。

  复杂度 \(\mathcal O(n\log n)\)。不过这里作者偷懒用 std::map 记录了每个环的 \(sum\)，写得好看一点是可以在这一部分做到 \(\mathcal O(n)\)。但求走进点双的第一个点似乎必须用带 \(\log\) 的算法 owo？

\(\mathcal{Code}\)

#include <map>
#include <cstdio>
#include <algorithm>

#define adj( g, u, v, c ) \
	for ( int eid = g.head[u], v, c; v = g.to[eid], c = g.cst[eid], eid; eid = g.nxt[eid] )

const int MAXN = 2e4, MAXM = 4e4;
int n, m, q, snode, fa[MAXN + 5][15];
int dfc, top, dfn[MAXN + 5], low[MAXN + 5], stk[MAXN + 5];
int dep[MAXN + 5], dis[MAXN + 5], root[MAXN + 5];
std::map<int, int> sum[MAXN + 5];

struct Graph {
	int ecnt, head[MAXN + 5], to[MAXM + 5], cst[MAXM + 5], nxt[MAXM + 5];
	inline void link ( const int s, const int t, const int c ) {
		to[++ ecnt] = t, cst[ecnt] = c, nxt[ecnt] = head[s];
		head[s] = ecnt;
	}
	inline void add ( const int u, const int v, const int c ) {
		link ( u, v, c ), link ( v, u, c );
	}
} src, tre;

inline char fgc () {
	static char buf[1 << 17], *p = buf, *q = buf;
	return p == q && ( q = buf + fread ( p = buf, 1, 1 << 17, stdin ), p == q ) ? EOF : *p ++;
}

inline int rint () {
	int x = 0; char s = fgc ();
	for ( ; s < '0' || '9' < s; s = fgc () );
	for ( ; '0' <= s && s <= '9'; s = fgc () ) x = x * 10 + ( s ^ '0' );
	return x;
}

inline void wint ( const int x ) {
	if ( 9 < x ) wint ( x / 10 );
	putchar ( x % 10 ^ '0' );
}

inline int min_ ( const int a, const int b ) { return a < b ? a : b; }

inline bool chkmin ( int& a, const int b ) { return b < a ? a = b, true : false; }

inline bool chkmax ( int& a, const int b ) { return a < b ? a = b, true : false; }

inline int cost ( const Graph& g, const int s, const int t ) {
	adj ( g, s, u, c ) if ( u == t ) return c;
	return -1;
}

inline int mncost ( const int id, int u, int v ) {
	int t1 = sum[id][u], t2 = sum[id][v];
	if ( t1 > t2 ) t1 ^= t2 ^= t1 ^= t2;
	return min_ ( t2 - t1, sum[id][root[id]] - ( t2 - t1 ) );
}

inline void buildSquare ( const int rt, const int p, const int sid ) {
	int beg = top; for ( ; stk[beg] ^ p; -- beg );
	root[sid] = rt;
	// loop: rt - stk[beg] - stk[beg + 1] - ... - stk[top] - rt.
	for ( int i = beg, cur = p, pre = rt; i <= top; pre = cur, cur = stk[++ i] ) {
		sum[sid][cur] = sum[sid][pre] + cost ( src, pre, cur );
	}
	sum[sid][rt] = sum[sid][stk[top]] + cost ( src, stk[top], rt );
	int u;
	do {
		u = stk[top --];
		tre.add ( sid, u, mncost ( sid, rt, u ) );
	} while ( u ^ p );
}

inline void Tarjan ( const int u, const int fa ) {
	dfn[u] = low[u] = ++ dfc, stk[++ top] = u;
	adj ( src, u, v, c ) if ( v ^ fa ) {
		if ( ! dfn[v] ) {
			Tarjan ( v, u ), chkmin ( low[u], low[v] );
			if ( low[v] >= dfn[u] ) {
				tre.add ( u, ++ snode, 0 );
				buildSquare ( u, v, snode );
			}
		} else chkmin ( low[u], dfn[v] );
	}
}

inline void init ( const int u, const int f ) {
	dep[u] = dep[fa[u][0] = f] + 1;
	for ( int i = 1; i <= 14; ++ i ) fa[u][i] = fa[fa[u][i - 1]][i - 1];
	adj ( tre, u, v, c ) if ( v ^ f ) {
		dis[v] = dis[u] + c;
		init ( v, u );
	}
}

inline int calcLCA ( int u, int v ) {
	if ( dep[u] < dep[v] ) u ^= v ^= u ^= v;
	for ( int i = 14; ~ i; -- i ) if ( dep[fa[u][i]] >= dep[v] ) u = fa[u][i];
	if ( u == v ) return u;
	for ( int i = 14; ~ i; -- i ) if ( fa[u][i] ^ fa[v][i] ) u = fa[u][i], v = fa[v][i];
	return fa[u][0];
}

inline int climb ( int u, const int tar ) {
	for ( int i = 14; ~ i; -- i ) if ( dep[fa[u][i]] > dep[tar] ) u = fa[u][i];
	return u;
}

int main () {
	n = snode = rint (), m = rint (), q = rint ();
	for ( int i = 1, u, v, w; i <= m; ++ i ) {
		u = rint (), v = rint (), w = rint ();
		src.add ( u, v, w );
	}
	Tarjan ( 1, 0 );
	init ( 1, 0 );
	for ( int u, v; q --; ) {
		u = rint (), v = rint ();
		int w = calcLCA ( u, v );
		if ( w <= n ) wint ( dis[u] + dis[v] - 2 * dis[w] );
		else {
			int pu = climb ( u, w ), pv = climb ( v, w );
			wint ( dis[u] - dis[pu] + dis[v] - dis[pv] + mncost ( w, pu, pv ) );
		}
		putchar ( '\n' );
	}
	return 0;
}