NKOJ-4573 Falsita

问题描述：

到海边了呢......
如果没有那次选择,现在是不是会好些呢......
都过去了。
仰望着星空,迎面吹过一阵阵海风,倚靠着护栏,Fine 在海边静静地伫立着,在一个个无际的长夜后,Fine 终于放下了往事的痛楚,得到了治愈。
但是作为 Fine 的另一重人格的 Falsita 就没那么幸运了。她仍然被各种繁忙的事务困扰着。
虽然同在一副躯体中,Fine 与 Falsita 的精神世界却相差甚远,Fine 可以轻易地构造出幻梦时,Falsita 却只能停留在现实的痛楚中。
但是为了生活需要,她们还是需要经常达成共识。
让我们形式化的描述一下吧。
她们所在的精神世界是一棵以 1 号节点为根的树,每个树上的节点 u 都有一个权值Wu,她们每个人分别都在一个节点上,达成共识的方法就是两个人都到达一个共识节点(即到达它们的最近公共祖先)。
一个点 u 与另外一个点 v 之间想要达到共识需要花费的代价为Wu+Wv。
有时两人的精神有所触动时,有时点的权值会改变成某个数,有时以某个点的子树中的所有点的权值会加上某个数。
Falsita 和 Fine 经常需要达成共识,每一次询问,已知达成的共识节点,求她们花费的期望代价。

输入格式：

输入共 m + 3 行。
第一行两个整数 n, m ,表示节点个数和操作数。
第二行 n - 1 个整数Pi,表示节点 i ( i = 2 . . . n ) 的父亲节点的编号。
第三行 n 个整数Wi。
接下来 m 行,每行表示一个操作。
1. S u delta 表示将节点 u 的权值加上 delta 。
2. M u delta 表示将以节点 u 为根的子树中的所有节点的权值加上 delta。
3. Q u 表示询问共识节点为 u 时的答案。
询问保证 u 不是叶子节点。

输出格式：

对于每组询问,输出答案,答案精确到小数点后 6 位。
你的程序输出的答案需要与标准答案之差不超过10^(-5)。

数据范围：

对于 100% 的数据,1 ≤ n, m ≤ 300000, 0≤ |delta|, |Wi|≤ 20000。

　　这道题思维很“巧妙”，代码细节也“巨多”，真是道“好题”。

　　

　　首先，题目要求求 期望值 ，期望值 =  点对数值总和 / 点对数量，这肯定不能暴力，我们需要推个具有普适性的式子来优化一下，由于这是个纯数学问题，这里就不赘述了，直接给出最终式子：

V[x]=Sum[x]*Size[x]-∑Sum[y]*Size[y]-W[x]
Div[x]=(Size[x]*Size[x]-∑Size[y]*Size[y]-1)/2

其中：y为x的儿子，V[x]为以x为根的子树中点对数值总和，Div[x]为子树中点对数量，Sum[x]为子树中所以点值之和，Size[x]为子树中节点数量，W[x]为点x的值

　　注意：上式子中的 W[ ] 为当时的点权，并不是初始值

　　先DFS一次，预处理出 V[ ] 和 Div[ ] 。

接下来，我们来分析 3种 操作：

　　操作1.单点修改：

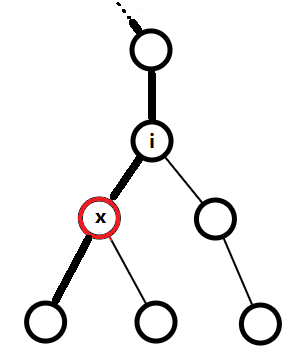
　　　　我们将点x加上一个Del，那么显然 V[ x ] += Del * Size[ i ]，而这并不会对x的儿子们产生任何影响，只会对从Root到x路径上的点产生影响。设 i 为从Root到x路径上的点，则 V[ Fa [ i ] ] += Del * ( Size [ Fa [ i ] ] - Size [ i ] )。

　　　　但是，这样操作，最坏的情况下可能达到 O(n) 的复杂度，怎么优化呢？

　　　　对一条数上的路径进行操作，我们很容易就想到了 树链剖分 ，对于一条重链而言，Size [ Fa [ i ] ] - Size [ i ] 是一个定值，知道 Del 就能求出 V [ ] 的变化量，可以线段树记下（记为Del1）；而对于一个轻边，暴力加就可以。即：

[ Id[Top[x]] , Id[x] )  区间修改 +=Del    //注意开闭

V[Fa[Top[x]]] += Del*(Size[Fa[Top[x]]]-Size[Top[x]])

　　　　树剖有一个重要的性质： 从一点到根的路径上，轻边数量不超过 log(n) ，重链数量不超过 log(n) 。所以，复杂度就成了 O(log n) 了。

　　操作2.子树修改：

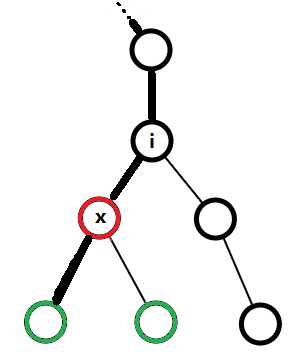
　　　　将以x为根的子树加上一个Del，这可以等价于：对每个子树中的点进行一次“操作1”，但这样复杂度又是 O(n) 的了。我们可以将这个操作的影响分成两类讨论：对子树的影响 和 对从Root到x路径上的点的影响。

　　　　先讨论对子树的影响：每个点点权增加Del，那么每个点对的贡献就会增加 2 * Del ，由于我们进行了树剖，所以一个子树的 Id[ ] 是连续的，所以再在线段树树记一下就可以了（记为Del2）； 然后再看对从Root到x路径上的点的影响，因为子树修改的本质是 对每个子树中的点进行一次“操作1” ，所以，对路径的影响可以等价于将x点点权增加 Del * Size [ x ]，这就转换成“操作1”了。具体来说：

[ Id[x] , Id[x]+Size[x]-1 ) 区间修改 += 2*Del     //注意开闭

操作1: S  x  d*Size[x]

（Ps：操作1 和 操作2 是分开记的）

　　操作3.查询：

　　　　经过上面的操作，查询就很简单了：

Ans = 2.0* ( V[x]+Del1*(Size[x]-Size[Son[x]]) ) / Div[x] + Del2
其中，Del1、Del2为线段树中维护的值
Ps:为保证精度，Div[ ]没有除以2，而是在求答案时进行处理

　　最后说一下代码的细节：区间的开闭一定要搞清楚再写！！！

　　（由于要进行树剖，所以预处理的DFS可以合入树剖的DFS中。）

Code:

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define int long long
using namespace std;
char IP;
int n,m,W[300005],V[300005],Sum[300005],Div[300005],Size[300005],Fa[300005],Som[300005],Son[300005],Deep[300005],Trans[300005],Id[300005],Top[300005],Cnt,Head[300005],Next[300005],To[300005];
struct node {int L,R,Del1,Del2,Lazy1,Lazy2;}Tr[2400005];
struct nodden {int Del1,Del2;}Tmp;
inline int read()
{
    int x(0),f(1);char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return f*x;
}
inline void ADD(int x,int y) {Next[++Cnt]=Head[x],Head[x]=Cnt,To[Cnt]=y;}
inline void DFS1(int x,int fa,int deep)
{
    int Max(0);
    Size[x]=1,Fa[x]=fa,Deep[x]=deep,Div[x]=-1,Sum[x]=W[x],V[x]=-W[x];
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        DFS1(j,x,deep+1),Size[x]+=Size[j],Div[x]-=Size[j]*Size[j],Sum[x]+=Sum[j],V[x]-=Size[j]*Sum[j];
        if(Size[j]>Max) Max=Size[j],Son[x]=j;
    }
    Div[x]+=Size[x]*Size[x],V[x]+=Sum[x]*Size[x];
}
inline void DFS2(int x,int anc)
{
    Top[x]=anc,Id[x]=++Cnt,Trans[Cnt]=x;
    if(Son[x]) DFS2(Son[x],anc);
    for(register int i=Head[x],j;i;i=Next[i])
    {
        j=To[i];
        if(j==Son[x]) continue;
        DFS2(j,j);
    }
    Som[x]=Cnt;
}
inline void Build(int x,int L,int R)
{
    Tr[x].L=L,Tr[x].R=R;
    if(L==R) return;
    int M=(L+R)>>1;
    Build(x<<1,L,M),Build(x<<1|1,M+1,R);
}
inline void PutDown1(int x) {Tr[x<<1].Del1+=Tr[x].Lazy1,Tr[x<<1].Lazy1+=Tr[x].Lazy1,Tr[x<<1|1].Del1+=Tr[x].Lazy1,Tr[x<<1|1].Lazy1+=Tr[x].Lazy1,Tr[x].Lazy1=0;}
inline void PutDown2(int x) {Tr[x<<1].Del2+=Tr[x].Lazy2,Tr[x<<1].Lazy2+=Tr[x].Lazy2,Tr[x<<1|1].Del2+=Tr[x].Lazy2,Tr[x<<1|1].Lazy2+=Tr[x].Lazy2,Tr[x].Lazy2=0;}
inline void ReModify(int x,int L,int R,int d)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) {Tr[x].Del1+=d,Tr[x].Lazy1+=d;return;}
    if(L<=Tr[x<<1].R) ReModify(x<<1,L,R,d);
    if(Tr[x<<1|1].L<=R) ReModify(x<<1|1,L,R,d);
}
inline void ReChange(int x,int L,int R,int d)
{
    if(L<=Tr[x].L&&Tr[x].R<=R) {Tr[x].Del2+=d,Tr[x].Lazy2+=d;return;}
    if(L<=Tr[x<<1].R) ReChange(x<<1,L,R,d);
    if(Tr[x<<1|1].L<=R) ReChange(x<<1|1,L,R,d);
}
inline nodden Find(int x,int pos)
{
    if(Tr[x].L==Tr[x].R) return nodden{Tr[x].Del1,Tr[x].Del2};
    if(Tr[x].Lazy1) PutDown1(x);if(Tr[x].Lazy2) PutDown2(x);
    if(pos<=Tr[x<<1].R) return Find(x<<1,pos);
    return Find(x<<1|1,pos);
}
inline void Modify(int x,int z)
{
    if(x==1) return;
    while(Top[x]!=1) ReModify(1,Id[Top[x]],Id[Fa[x]],z),V[Fa[Top[x]]]+=z*(Size[Fa[Top[x]]]-Size[Top[x]]),x=Fa[Top[x]];
    if(x!=1) ReModify(1,1,Id[Fa[x]],z);
}
inline void Change(int x,int z) {ReChange(1,Id[x],Id[x]+Size[x]-1,2*z),Modify(x,z*Size[x]);}
inline double GetAns(int x)
{
    Tmp=Find(1,Id[x]),V[0]=V[x]+Tmp.Del1*(Size[x]-Size[Son[x]]);
    return 2.0*V[0]/Div[x]+Tmp.Del2;
}
signed main()
{
    n=read(),m=read();
    for(register int i=2,x;i<=n;++i) x=read(),ADD(x,i);
    for(register int i=1;i<=n;++i) W[i]=read();
    Cnt=0,DFS1(1,0,1),DFS2(1,1),Build(1,1,n);
    for(register int i=1,x,y;i<=m;++i)
    {
        scanf(" %c",&IP);
        switch(IP)
        {
            case 'S':{x=read(),y=read(),V[x]+=y*Size[x]-y,Modify(x,y);break;}
            case 'M':{x=read(),y=read(),Change(x,y);break;}
            case 'Q':{x=read(),printf("%.6lf\n",GetAns(x));break;}
        }
    }
    return 0;
} 

Falsita