夜莺与玫瑰

题解

联赛$T1$莫比乌斯$\%\%\%$

$dead$  $line$是直线

首先横竖就是$n+m$这比较显然

枚举方向向量

首先我们枚举方向向量时只枚举右下方向,显然贡献$*2$就是所有斜着的直线

$i,j$表示当自己向右$i$个单位长度,向下$j$单位长度

我们相同斜率下只算最短的线贡献,(因为其他长度下方案数都包含在最短里面了)

我们方向向量$i$,$j$的$gcd(i,j)==1$时我们枚举的才是当前斜率最短长度,

然后考虑贡献

考虑容斥,先算出来当前长度下所有线段再减去重合的

$(n-a)*(m-b)$是总方案数,考虑重合部分

假设我们有一个4*4点阵

. . . .

. . . .

. . . .

. . . .

我们算1,1方向向量贡献

\ \ \ .

\ \ \ \

\ \ \ \

. \ \ \

只有

\ \ \ .

\ \ \ \

\ \ \ \

. \ \ \

标蓝才有贡献,别的都是算重的

定义前趋为$x-1$ $y-1$,后继$x+1$ $y+1$

观察这些线发现符合条件就是前趋不在点阵而后继在点阵数量

例如$1$,$1$这个点$+$方向向量得到$-1$ $-1$ 和$2$ $2$

因为$-1$ $-1$不在点阵内所以是合法的

,我们把他们都提到与边界相重

看他们相减后是否在边界中即可

重复的部分就是$max((n-2*a),0)*max((m-2*b),0)$

$\sum\limits_ {a=1}^{a<=n} \sum\limits_{b=1}^{b<=m} [gcd(a,b)==1](n-a)*(m-b)-max((n-2*a),0)*max((m-2*b),0)$

这样我们还是$AC$不了$T=10000$稍巨

所以我们预处理一下,让查询变成$O(n)$的$(其实可以是O(1))然而出题人还卡空间$

把原式子拆成$(n-a)*m-(n-a)*b$每一个$gcd(a,b)==1$都会对第一个式子造成贡献,而后面那个式子就是$(n-a)*{\sum\limits_{b=1}^{b<=m} [gcd(a,b)==1] b}$

维护前缀和$tot(a,m)$表示$b=1--m所有数中$与$a$,$gcd==1$的个数和为$tot(a,m)$,

$sum(a,m)$表示$b=1--m$中所有$gcd(a,b)==1$对应$\sum\limits_{b=1}^{b<=m} [gcd(a,b)==1] b$和为$sum(a,m)$

所以式子$\sum\limits_ {a=1}^{a<=n} \sum\limits_{b=1}^{b<=m} [gcd(a,b)==1](n-a)*(m-b)$可以化为$(n-a)*(tot(a,m)*m-sum(a,m))$

后面这个式子类似

首先如果$(n-2*a)<=0$或$(m-2*b)<=0$就不用减了

所以$m-2*b>0$才可以即$b<\frac{m}{2}$

所以后面式子可以化为$(n-2*a)*(tot(a,\frac{m}{2})*m-2*sum(a,\frac{m}{2}))$

总式子就是$\sum\limits_{a=1}^{a<=n} (n-a)*(tot(a,m)*m-sum(a,m))-(n-2*a)*(tot(a,\frac{m}{2})*m-2*sum(a,\frac{m}{2}))$

单单是这样你还是$AC$不了$4000*4000$枚举$gcd$很慢,你需要递推

代码

  1. #include<iostream>
  2. #include<cstdio>
  3. using namespace std;
  4. int T,n,m,sum[4100][4100];
  5. const int mod=1073741824;
  6. short num[4100][4100],g[4100][4100];
  7. int gcd(int a,int b){return b?gcd(b,a%b):a;}
  8. int main(){
  9.     for(register int i=1;i<=4001;i++){
  10.         g[i][i]=g[0][i]=g[i][0]=i;
  11.         for(register int j=1;j<i;j++){
  12.             g[i][j]=g[j][i]=g[j][i%j];
  13.         }
  14.     }
  15.     for(register int i=1;i<=4001;i++){
  16.         for(register int j=1;j<=4001;j++){
  17.             sum[i][j]=sum[i][j-1];
  18.             num[i][j]=num[i][j-1];
  19.             if(g[i][j]==1) sum[i][j]=(sum[i][j]+j)%mod,num[i][j]++;
  20.         }
  21.     }
  22.     scanf("%d",&T);
  23.     while(T--){
  24.         scanf("%d%d",&n,&m);
  25.         long long ans=0;
  26.         for(register int i=1;i<n;i++){
  27.             ans=(ans+(num[i][m]*m%mod-sum[i][m]%mod)*(n-i)%mod)%mod;
  28.             if(2*i<n) ans=ans-(num[i][m/2]*m%mod-2*sum[i][m/2]%mod)*(n-i*2)%mod;
  29.         }
  30.         ans=(ans*2%mod+n+m)%mod;
  31.         printf("%lld\n",(ans+mod)%mod);
  32.     }
  33. }

夜莺

玫瑰花精

题解

抱歉,题解没时间写了

  1. 对于 100%的数据
  2. 可以考虑线段树。首先我们对区间[1..n]建立一棵线段树。对于每一个节点,
  3. 维护 4 个值。分别是 l,r,mid,p。l 表示在当前结点线段树所在区间最左边的花精所在的位置,r 表示最右边的花精所在的位置。mid 表示在这个小区间[l,r]中的
  4. 两只花精之间的最长距离除以 2 后的值。p 表示取 mid 值时所在的紧邻的两只
  5. 花精的中间位置,也就是在[l,r]中的答案值。
  6. 对于 1 询问:访问线段树的第一个节点,我们比较 l-1,n-r,mid 的值哪
  7. 个更大,就选哪个,它们的答案依次是 1,n,p。假设我们求得的位置是 fairy[x]。
  8. 然后访问[fairy[x],fairy[x]]所在的线段树的叶子节点,初始化它的值,然后回溯,
  9. 进行合并。对于 tr[x].l 与 tr[x].r 可以通过两个儿子的 l,r 信息得出。对于 tr[x].mid
  10. 值,首先在左右儿子的 mid 值中去一个最大的值。其次考虑一种情况,就是夹在
  11. 两个线段之间的距离,可以通过(tr[x+x+1].l-tr[x+x].r) / 2 的值得出在于 mid
  12. 进行比较,然后 p 就随着 mid 的值的更新而更新。
  13. 对于 2 询问:访问询问花精所在的位置,直接将它的叶子节点
  14. [fairy[x],fairy[x]]删除,然后回溯时,再做一次合并操作。

代码

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define ll long long
  4. #define A 1010101
  5. struct tree{
  6.     ll l,r,mid,ql,qr,p;
  7. }tr[A];
  8. ll n,m;
  9. ll in[A];
  10. void built(ll x,ll l,ll r){
  11.     tr[x].l=l,tr[x].r=r;
  12.     if(l==r){
  13.         return ;
  14.     }
  15.     ll mid=(l+r)>>1;
  16.     built(x<<1,l,mid);
  17.     built(x<<1|1,mid+1,r);
  18. }
  19. void update(ll x){
  20. //    printf("ql=%lld qr=%lld\n",tr[x].ql,tr[x].qr);
  21.     if(tr[x<<1].ql) tr[x].ql=tr[x<<1].ql;
  22.     else  tr[x].ql=tr[x<<1|1].ql;
  23.     if(tr[x<<1|1].qr) tr[x].qr=tr[x<<1|1].qr;
  24.     else  tr[x].qr=tr[x<<1].qr;
  25.     tr[x].mid=tr[x<<1].mid;
  26.     tr[x].p=tr[x<<1].p;
  27.     if(tr[x<<1].qr&&tr[x<<1|1].ql){
  28. //        ll minn=tr[x].mid;
  29.         if((tr[x<<1|1].ql-tr[x<<1].qr)/2>tr[x].mid){
  30.             tr[x].mid=(tr[x<<1|1].ql-tr[x<<1].qr)>>1;
  31.             tr[x].p=(tr[x<<1].qr+tr[x<<1|1].ql)>>1;
  32. //            minn=tr[x].mid;
  33.         }
  34.         if(tr[x<<1|1].mid>tr[x].mid){
  35.             tr[x].mid=tr[x<<1|1].mid;
  36.             tr[x].p=(tr[x<<1|1].p);
  37. //            minn=tr[x].mid;
  38.         }
  39.     }
  40. //    printf("x=%lld l%lld--r%lld <<1%lld %lld |1%lld %lld区间 leftson mid=%lld mid=%lld x.mid=%lld p=%lld p=%lld p=%lld \n",x,tr[x].ql,tr[x].qr,tr[x<<1].ql,tr[x<<1].qr,tr[x<<1|1].ql,tr[x<<1|1].qr,tr[x<<1].mid,tr[x<<1|1].mid,tr[x].mid,tr[x].p,tr[x<<1].p,tr[x<<1|1].p);
  41.     return ;
  42. }
  43. void change(ll x,ll pla,ll val){
  44.     if(tr[x].l==tr[x].r){
  45.         if(val==1){
  46.             tr[x].ql=tr[x].l;
  47.             tr[x].qr=tr[x].r;
  48. //            printf("x=%lld l=%lld r=%lld\n",x,tr[x].l,tr[x].r);
  49.             tr[x].p=0;
  50.             tr[x].mid=0;
  51.             return ;
  52.         }
  53.         else {
  54.             tr[x].ql=0,
  55.             tr[x].qr=0,
  56.             tr[x].p=0,
  57.             tr[x].mid=0;
  58. //            printf("x=%lld ql=%lld qr=%lld\n",x,tr[x].ql,tr[x].qr);
  59.             return ;
  60.         }
  61.     }
  62.     ll mid=(tr[x].l+tr[x].r)>>1;
  63.     if(mid>=pla) change(x<<1,pla,val);
  64.     else change(x<<1|1,pla,val);
  65.     update(x);
  66. }
  67. int main(){
  68.     scanf("%lld%lld",&n,&m);
  69.     built(1,1,n);
  70.     for(ll i=1,opt,a,b;i<=m;i++){
  71.         scanf("%lld%lld",&opt,&a);
  72.         if(opt==1){
  73.             if(tr[1].ql==0){
  74.                 in[a]=1;
  75.                 printf("%lld\n",in[a]);
  76.                 change(1,in[a],1);
  77.                 continue ;
  78.             }
  79.             ll minn=-0x7ffffff;
  80. //            printf("mid=%lld ql-1=%lld n-qr=%lld\n",tr[1].mid,tr[1].ql-1,n-tr[1].qr);
  81.             if(tr[1].ql-1>minn){
  82.                 minn=tr[1].ql-1;
  83.                 in[a]=1;
  84.             }
  85.             if(tr[1].mid>minn){
  86.                 minn=tr[1].mid;
  87.                 in[a]=tr[1].p;
  88.             }
  89.             if(n-tr[1].qr>minn){
  90.                 minn=n-tr[1].qr;
  91.                 in[a]=n;
  92.             }
  93.             printf("%lld\n",in[a]);
  94.             change(1,in[a],1);
  95.         }
  96.         else change(1,in[a],-1);
  97.     }
  98. }

影子

题解

以为是神仙$dp$,然后是神仙并查集,

觉得官方题解写的很明白

将所有点按照权值从大到小排序,对于当前点和比当前点权值大的点和并到一个集合内,并查集维护当前集合直径和对应端点,

合并两个并查集时当前直径可以是其中一个集合中直径或两个集合交叉取

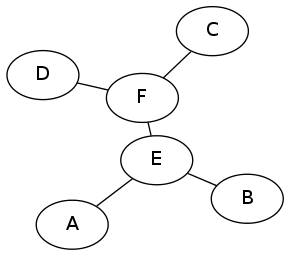
例如集合$AEB$ $CDF$ 合并时直径可以是$A-C$ $A-D$ $B-C$ $B-D$ (交叉取)$A-B$,$C-D$(原本集合)

需要用到两点之间距离$lca$在线回答就行了

合并并查集时$ans=max(ans,直径长度*a[i])$

一个问题是当前点是否在集合内,其实并不会造成影响,你已经将点从大到小排好序了,你当前枚举如果之前出现过那么已经在之前处理过了

代码

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define ll long long
  4. #define A 500000
  5. struct moo{
  6.     ll l,r,len,fa;
  7. }fa[A];
  8. struct vvv{
  9.     ll v,id;
  10.     friend bool operator < (const vvv & a,const vvv & b){
  11.         return a.v>b.v;
  12.     }
  13. }v[A];
  14. ll dis[A],f[A][25],head[A],nxt[A],ver[A],edg[A],deep[A],va[A];
  15. ll t,n,m,ans=0,tot=0;
  16. void add(ll x,ll y,ll z){
  17.     nxt[++tot]=head[x],head[x]=tot,ver[tot]=y,edg[tot]=z;
  18. }
  19. ll find(ll x){
  20. //    printf("%lld.fa=%lld\n",x,fa[x].fa);
  21.     if(x!=fa[x].fa)
  22.         fa[x].fa=find(fa[x].fa);
  23.     return fa[x].fa;
  24. }
  25. inline ll lca(ll x,ll y)
  26. {
  27.     if(deep[x]>deep[y])swap(x,y);
  28.     for(ll i=t;i>=0;i--)
  29.     {
  30.         if(deep[x]==deep[y]) break;
  31.         if(deep[x]<=deep[f[y][i]]) y=f[y][i];
  32.     }
  33.     if(x==y) return x;
  34.     for(ll i=t;i>=0;i--)
  35.         if(f[x][i]!=f[y][i])
  36.             x=f[x][i],y=f[y][i];
  37.     return f[x][0];
  38. }
  39. void merge(ll x,ll y,ll edgval,ll now){
  40.     ll maxx=0;
  41.     x=find(fa[x].fa),y=find(fa[y].fa);
  42.     fa[y].fa=x;
  43.     ll l1=fa[x].l,r1=fa[x].r,l2=fa[y].l,r2=fa[y].r;
  44.     ll dis1=fa[x].len,
  45.        dis2=fa[y].len,
  46.        dis3=dis[l1]+dis[l2]-2*dis[lca(l1,l2)],
  47.        dis4=dis[l1]+dis[r2]-2*dis[lca(l1,r2)],
  48.        dis5=dis[r1]+dis[l2]-2*dis[lca(r1,l2)],
  49.        dis6=dis[r1]+dis[r2]-2*dis[lca(r1,r2)];
  50.     if(dis2>fa[x].len){
  51.         fa[x].l=l2,fa[x].r=r2;
  52.         fa[x].len=dis2;
  53.     }
  54.     if(dis3>fa[x].len){
  55.         fa[x].l=l1,fa[x].r=l2;
  56.         fa[x].len=dis3;
  57.     }
  58.     if(dis4>fa[x].len){
  59.         fa[x].l=l1,fa[x].r=r2;
  60.         fa[x].len=dis4;
  61.     }
  62.     if(dis5>fa[x].len){
  63.         fa[x].l=r1,fa[x].r=l2;
  64.         fa[x].len=dis5;
  65.     }
  66.     if(dis6>fa[x].len){
  67.         fa[x].l=r1,fa[x].r=r2;
  68.         fa[x].len=dis6;
  69.     }
  70.     ans=max(ans,fa[x].len*va[now]);
  71. //    printf("l1=%lld r1=%lld l2=%lld r2=%lld  dis1=%lld dis2=%lld dis3=%lld dis4=%lld dis5=%lld dis6=%lld fa[x].len*va[now]=%lld dis[l1]=%lld+dis[l2]=%lld-2*dis[lca(l1,l2)]=%lld %lld lca=%lld ve[%lld]=%lld\n",l1,r1,l2,r2,dis1,dis2,dis3,dis4,dis5,dis6,fa[x].len*va[now],dis[r1],dis[r2],2*dis[lca(r1,r2)],dis[r1]+dis[r2]-2*dis[lca(r1,r2)],lca(r1,r2),now,va[now]);
  72. }
  73.  
  74. void dfs(ll x,ll pre,ll de){
  75.     deep[x]=de;
  76.     for(ll i=head[x];i;i=nxt[i]){
  77.         ll y=ver[i];
  78.         if(y==pre) continue ;
  79.         dis[y]=dis[x]+edg[i];
  80.         f[y][0]=x;
  81.         dfs(y,x,de+1);
  82.     }
  83. }
  84. void mem(){
  85.     memset(head,0,sizeof(head));
  86.     memset(fa,0,sizeof(fa));
  87.     tot=0;
  88.     ans=0;
  89. }
  90. int main(){
  91. //    freopen("b.in","r",stdin);
  92.     ll T;
  93.     scanf("%lld",&T);
  94.     while(T--){
  95.         scanf("%lld",&n);
  96.         mem();
  97.         t=log(n)/log(2)+1;
  98.         for(ll i=1;i<=n;i++){
  99.             scanf("%lld",&v[i].v);
  100.             v[i].id=i;
  101.             va[i]=v[i].v;
  102.             fa[i].fa=i;
  103.             fa[i].l=fa[i].r=i;
  104.         }
  105.     //    printf("n=%lld\n",n);
  106.         for(ll i=1,a,b,c;i<=n-1;++i){
  107.             scanf("%lld%lld%lld",&a,&b,&c);
  108.             add(a,b,c),add(b,a,c);
  109.         }
  110.  
  111.         dfs(1,0,0);
  112.         f[1][0]=1;
  113.         for(ll j=1;j<=t;j++)
  114.             for(ll i=1;i<=n;i++)
  115.                 f[i][j]=f[f[i][j-1]][j-1];
  116.         sort(v+1,v+n+1);
  117.         for(ll i=1;i<=n;i++){
  118.             ll x=v[i].id,val=v[i].v;
  119.             for(ll j=head[x];j;j=nxt[j]){
  120.                 ll y=ver[j];
  121.                 if(va[y]>=va[x]){
  122.                     merge(x,y,edg[j],x);
  123.  
  124.                 }
  125.             }
  126.         }
  127.         printf("%lld\n",ans);
  128.     }
  129. }

csp-s模拟测试41「夜莺与玫瑰·玫瑰花精·影子」的更多相关文章

  1. NOIP模拟测试2「排列 （搜索）·APIO划艇」

    排序 内存限制:128 MiB 时间限制:1000 ms 标准输入输出     题目描述 输入格式 数据范围与提示 对于30%的数据,1<=N<=4: 对于全部的数据,1<=N< ...

  2. NOIP模拟测试19「count·dinner·chess」

    反思: 我考得最炸的一次 怎么说呢?简单的两个题0分,稍难(我还不敢说难,肯定又有人喷我)42分 前10分钟看T1,不会,觉得不可做,完全不可做,把它跳了 最后10分钟看T1,发现一个有点用的性质,仍 ...

  3. [考试反思]0909csp-s模拟测试41：反典

    说在前面:我是反面典型!!!不要学我!!! 说在前面:向rank1某脸学习,不管是什么题都在考试反思后面稍微写一下题解. 这次是真的真的运气好... 这次知识点上还可以,但是答题策略出了问题... 幸 ...

  4. [CSP-S模拟测试41]题解

    中间咕的几次考试就先咕着吧…… A.夜莺与玫瑰 枚举斜率.只考虑斜率为正且不平行于坐标轴的直线,最后把$ans\times 2$再$+1$即可. 首先肯定需要用$gcd(i,j)==1$确保斜率的唯一 ...

  5. csp-s模拟测试44「D·E·F」

    用心出题,用脚造数据 乱搞场 1 #include<bits/stdc++.h> 2 #define re register 3 #define int long long 4 #defi ...

  6. NOIP模拟测试30「return·one·magic」

    magic 题解 首先原式指数肯定会爆$long$ $long$ 首先根据欧拉定理我们可以将原式换成$N^{\sum\limits_{i=1}^{i<=N} [gcd(i,N)==1] C_{G ...

  7. NOIP模拟测试21「折纸&#183;不等式」

    折纸 题解 考试时无限接近正解,然而最终也只是接近而已了 考虑模拟会爆炸,拿手折纸条试一试,很简单 考你动手能力 代码 #include<bits/stdc++.h> using name ...

  8. NOIP模拟测试18「引子·可爱宝贝精灵·相互再归的鹅妈妈」

    待补 引子 题解 大模拟,注意细节 代码1 #include<bits/stdc++.h> using namespace std; int n,m;char a[1005][1005]; ...

  9. NOIP模拟测试10「大佬·辣鸡·模板」

    大佬 显然假期望 我奇思妙想出了一个式子$f[i]=f[i-1]+\sum\limits_{j=1}^{j<=m} C_{k \times j}^{k}\times w[j]$ 然后一想不对得容 ...

随机推荐

  1. 多种方法实现实现全排列 + sort调用标准函数库函数的简述

    全排列:所有不同顺序的元素组组成的一个集合.这里使用使用递归实现全排列. 使用递归算算法呢,首先我们先找一下结束的条件:我们要对一组元素(这里使用数字举例)实现全排列,临界条件就是递归到只有一个元素的 ...

  2. JS数组的操作方法汇总

    数组的增删 push():添加到最后 pop():取出最后一个 shift():取出第一个 unshift():添加到第一个 splice() : 返回删除的数组,如果没有则为空数组,会改变原数组.可 ...

  3. 三分钟了解B2B CRM系统的特点

    最近很多朋友想了解什么是B2B CRM系统,说到这里小Z先来给大家说说什么是B2B--B2B原本写作B to B,是Business-to-Business的缩写.正常来说就是企业与企业之间的生意往来 ...

  4. [MySQL数据库之数据库相关概念、MySQL下载安装、MySQL软件基本管理、SQL语句]

    [MySQL数据库之数据库相关概念.MySQL下载安装.MySQL软件基本管理.SQL语句] 数据库相关概念 数据库管理软件的由来 数据库管理软件:本质就是个C/S架构的套接字程序. 我们在编写任何程 ...

  5. 『动善时』JMeter基础 — 20、JMeter配置元件【HTTP Cookie管理器】详细介绍

    目录 1.HTTP Cookie管理器介绍 2.HTTP Cookie管理器界面详解 3.JMeter中对Cookie的管理 (1)Cookie的存储 (2)Cookie的管理策略 4.补充:Cook ...

  6. ES6对象的新增方法的使用

    Object.assign Object Object.assign(target, ...sources) 将所有可枚举属性的值从一个或多个源对象复制到目标对象 参数: target 目标对象 so ...

  7. prometheus nginx-module-vts删除内存区数据

    项目地址:https://github.com/vozlt/nginx-module-vts 删除所zone内存中的数据 curl localhost/status/control?cmd=delet ...

  8. date命令月日时分年

    # date +%Y/%m/%d2019/09/29[root@a-3e5 lpts-20190910-keyan-v0.2]# date +%H:%M20:00

  9. Linux 用 ps 與 top 指令找出最耗費 CPU 與記憶體資源的程式最占cpu的进程

    Linux 用 ps 與 top 指令找出最耗費 CPU 與記憶體資源的程式 2016/12/220 Comments  ######### ps -eo pid,ppid,%mem,%cpu,cmd ...

  10. 【转载】 Linux常用命令: zip、unzip 压缩和解压缩命令

    Linux常用命令: zip.unzip 压缩和解压缩命令   Linux常用命令: zip.unzip 压缩和解压缩命令 zip的用法 基本用法是: zip [参数] [打包后的文件名] [打包的目 ...