支持向量机(SVM)之硬阈值

支持向量机 ( support vector machine, SVM ) 是使用超平面来对给定的 p 维向量进行分类的非概率二元线性分类器。

一、超平面 ( hyperplane )

在一个p维的输入空间，超平面就是 \(p-1\) 维的子空间。比如：在一个二维输入的空间，超平面就是一维，也就是直线。用公式表示如下：

\[b + w_{1}x_{11} + w_{2}x_{12}=0
\]

在一个三维的输入空间，超平面就是二维，也就是一个平面，公式表示如下：

\[b + w_{1}x_{11} + w_{2}x_{12} + w_{3}x_{13}=0
\]

当输入维度 \(p ＞ 3\) 时，很难直观地理解超平面，但是可以简单地记为：超平面将输入空间分为两个部分，因此超平面最终的数学表达式为：

\[b + w_{1}x_{11} + w_{2}x_{12} +...+ w_{p}x_{1p} = 0
\]

其中，\(\alpha_{i}\) 表示超平面的参数。因此，超平面将一个p维的空间分成两个部分，考虑一个 \(p\) 维度的输入实例 \(x = (x_{1}, x_{2},..., x_{p})\)，当该实例在超平面上时，有：

\[b + w_{1}x_{11} + w_{2}x_{12} +...+ w_{p}x_{1p} = 0
\]

当其不在超平面上时，必然会存在：

\[b + w_{1}x_{11} + w_{2}x_{12} +...+ w_{p}x_{1p} > 0
\]

或者：

\[b + w_{1}x_{11} + w_{2}x_{12} +...+ w_{p}x_{1p} < 0
\]

二、使用超平面进行二分类

考虑到一系列的输入 \(x = (x_{1}, x_{2},...,x_{n})\)，其中 \(x_{i} = (x_{i1}, x_{i2},...,x_{ip})^{T}\) ，那么对应的标签 应该属于不同的类，这里用\((1, -1)\) 来表示，即：\(y = (y_{1}, y_{2},...,y_{n}) \in (-1, 1)\)。因此我们需要根据这些观测的训练数据 \(T = ( (x_{1},y_{1}), (x_{2},y_{2}),...,(x_{n},y_{n})\) 来学习到SVM的参数 \((\alpha_{1}, \alpha_{2},...,\alpha_{p})\)，使其能够对任意给定的 \(p\) 维输入 \(x_{n+1}\) 做出正确的判断。在训练过程中，假如在超平面一侧的为 \(-1\)，那么在另外一侧的就是 \(+1\)，于是训练的标准就可以表示为：

\[b + w_{1}x_{i1} + w_{2}x_{i2} +...+ w_{p}x_{ip} > 0,\quad if \quad y_{i}=1 \\
b + w_{1}x_{i1} + w_{2}x_{i2} +...+ w_{p}x_{ip} < 0,\quad if \quad y_{i}=-1
\]

因此，最终的训练标准可以统一为：

\[(b + w_{1}x_{i1} + w_{2}x_{i2} +...+ w_{p}x_{ip})y_{i}>0
\]

最终的超平面方程写成矩阵形式为：\(f(x) = w^{T}x + b\)

但是从理论上来讲通过旋转，平移等操作，满足这种条件的 SVM 分类器有无数个，如下图左边的部分所示，我们以二维输入为例，把蓝色的点看做同一类，而红色的点看做第二类，黑色的线就是学到的分类器，那么到底应该选哪一个呢？

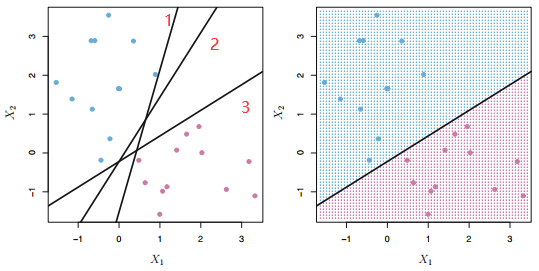
第1个分类器太靠近蓝色的和粉色的点，稍微有点扰动很有可能造成错误的分类，鲁棒性较差

第2，3个分类器似乎看起来还可以，但是选取的标准又该怎么定义呢？

一个很自然而然的想法就是选择最大边缘超平面\((maximal \quad margin \quad hyperplane)\)。即：我们可以计算 \(p\) 维空间上所有的点到该超平面的距离，另其最小的距离（\(margin\)）最大。由于离超平面越近的点越容易分不清楚，最大化这些距离之后便能具有一定程度的鲁棒性，这样一来便能找到最优的超平面。因此通过这种策略，上图的最优超平面可以描述为下图：

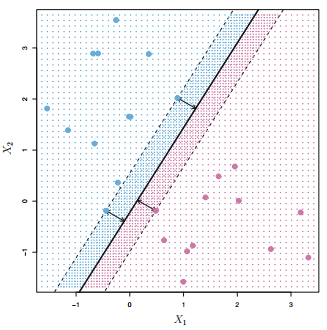
从上图中我们看到三个训练观测值与最大边距超平面等距，并且沿着指示边距宽度的虚线排列。因此这三个观测值被称为支持向量。有趣的是，最大边缘超平面直接取决于支持向量，而不取决于其他观测值，任何其他观察的移动不会影响分离超平面，前提是观察的移动不会导致它跨越 \(margin\)。

三、最大间隔阈值（\(maximum\quad margin\)）表示

回忆高中数学的相关内容，对于平面 \(\Phi:Ax+By+Cz+D=0\)，则其法向量为 \([A, B, C]\)，空间内任意一点 \((x,y,z)\) 到该平面的距离为：

\[distance = \dfrac{|Ax_{0}+By_{0}+Cz_{0}+D|}{\sqrt {A^{2}+B^{2}+C^{2}}}
\]

那么同理，在 \(p\) 维空间内，\(p-1\) 维超平面表示为：\(\Phi: w^{T}x = 0\)，则其法向量为 \(w^{T}\)，空间内任意一点 \(x_{i}^{T} = (x_{i1},x_{i2},...,x_{ip})\) 到该超平面的距离为：

\[distance = \dfrac{|w^{T}x_{i}+b|}{w^{2}} = \dfrac{|w^{T}x_{i}+b|}{||w||}
\]

加入超平面能够实现正确的分类，那么设支持向量到超平面的距离为 \(\beta\)，我们可以得到分类的值为：

\[(b + w_{1}x_{i1} + w_{2}x_{i2} +...+ w_{p}x_{ip})y_{i}>\beta
\]

即：\(w^{T}x > \beta\)，通过观察发现，缩放 \(w\) 的值并不会影响超平面的位置，因此不管 \(\beta\) 取任何值，最后都能通过 \(w'=w/\beta,\quad b'=b/\beta\) 将结果变为：\(w^{T}x+b > 1\)，因此支持向量之间的距离就变成了： \(2/||w||\)， 所以最后 SVM 的模型就变成了：

\[\mathop{argmax} \limits_{w} \dfrac{2}{||w||}\quad \quad s.t.\quad y_{i}(w^{T}x_{i}+b)>1,\quad x = 1, 2,...,m
\]

等价于：

\[\mathop{argmin} \limits_{w} \dfrac{1}{2}||w||^{2}\quad s.t.\quad y_{i}(w^{T}x_{i}+b)>1,\quad x = 1,2,...,m
\]

即：将超平面左右平移1个单位得到超平面 \(\Phi_{1}，\Phi_{2}\)，找出所有为 +1 类的点全部落在 \(\Phi_{1}\) 左侧，所有为 -1 类的点全部落在 \(\Phi_{2}\) 右侧，并且同时满足超平面的所有参数 \(w\) 的平方和最小的超平面。

四、对偶问题与KKT条件

求解带约束的不等式，根据拉格朗日乘数法将式 \((13)\) 改写成无约束不等式，得到：

\[L(w,b,\lambda) = \dfrac{1}{2}||w||^{2}+\sum_{i=1}^{m}\lambda_{i}(1-y_{i}(w^{T}x_{i}+b))
\]

于是我们对 \(L\) 求偏导：

\[\dfrac{\partial{L(w,b,\lambda)}}{\partial w} = w-\sum_{i=1}^{m}\lambda_{i}y_{i}x_{i}=0\\
\dfrac{\partial{L(w,b,\lambda)}}{\partial b} = \sum_{i=1}^{m}\lambda_{i}y_{i} = 0
\]

将得到的 \(w = \sum_{i=1}^{m}\lambda_{i}y_{i}x_{i},\quad \sum_{i=1}^{m}\lambda_{i}y_{i} = 0\) 代入式 \((14)\) 得到：

\[L(w,b,\lambda) = \dfrac{1}{2}(\sum_{i=1}^{m}\lambda_{i}y_{i}x_{i})^{T}\sum_{j=1}^{m}\lambda_{j}y_{j}x_{j}+\sum_{i=1}^{m}\lambda_{i} - \sum_{i=1}^{m}\lambda_{i}y_{i}(w^{T}x_{i})\\
=\dfrac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\lambda_{i}y_{i}\lambda_{j}y_{j}x_{i}^{T}x_{j}+\sum_{i=1}^{m}\lambda_{i} - \sum_{i=1}^{m}\sum_{j=1}^{m}\lambda_{i}y_{i}\lambda_{j}y_{j}x_{i}^{T}x_{j}\\
=\sum_{i=1}^{m}\lambda_{i} - \dfrac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\lambda_{i}y_{i}\lambda_{j}y_{j}x_{i}^{T}x_{j}
\]

即最后式子 \((14)\) 的对偶问题可以写成：

\[\mathop{argmax}\limits_{\lambda}\sum_{i=1}^{m}\lambda_{i} - \dfrac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\lambda_{i}y_{i}\lambda_{j}y_{j}x_{i}^{T}x_{j}, \quad s.t. \quad \sum_{i=1}^{m}\lambda_{i}y_{i} = 0
\]

最后通过求出 \(\lambda\) ，带入到公式 \((15)\) 中就可以求出 \(w\) ，进而能求出 \(b\)。

在上述将原问题转换为对偶问题的过程中，原问题需要满足 \(KKT\) 条件，即：

\[\begin{equation}
\left\{
\begin{array}{lr}
\lambda_{i}>=0; & \\
y_{i}f(x_{i})-1 >=0; & \\
\lambda_{i}(y_{i}f(x_{i})-1) = 0 ;
\end{array}
\right.
\end{equation}
\]

这个条件不就是同济第七版《高等数学》关于拉格朗日乘数法的应用前提吗？有兴趣的朋友可以自己查阅一下，毕竟已经不学数学好多年了，若有疏漏还请斧正。

这样就出现一个非常有趣的现象，即：

若 \(\lambda_{i}=0\)，则 \(y_{i}f(x_{i}) >= 1\)

若 \(\lambda_{i}>0\)，则 \(y_{i}f(x_{i}) = 1\)，所对应的样本刚好落在最大边界上 ( 即支持向量 )，因此训练完成后大部分的训练样本都不需要保留，最终模型仅仅与支持向量有关。

上述主要分析了当训练样本是线性可分的情况下，SVM的一些理论与求解过程，即硬阈值的SVM。当训练样本不是线性可分的情况下需要设计软阈值以及核函数的SVM，限于篇幅原因，将在后面的文章中进行阐述。