二叉查找树（BST)、平衡二叉树(AVL树)

二叉查找树(BST)

　　特殊的二叉树，又称为排序二叉树、二叉搜索树、二叉排序树。

　　二叉查找树实际上是数据域有序的二叉树，即对树上的每个结点，都满足其左子树上所有结点的数据域均小于或等于根结点的数据域，右子树上所有结点的数据域均大于根结点的数据域。如下图所示：

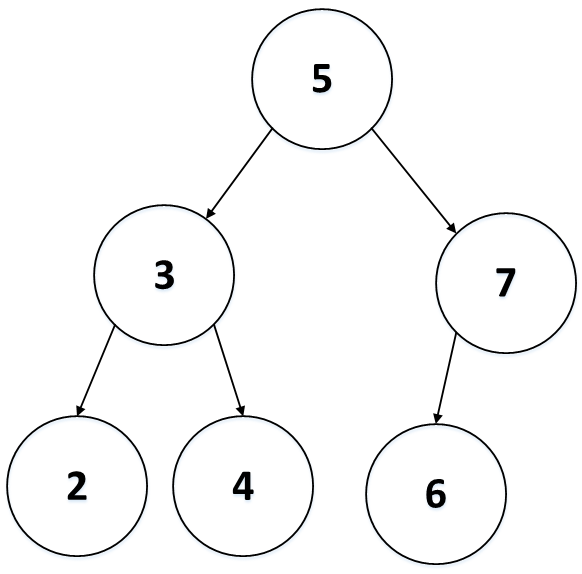
二叉查找树通常包含查找、插入、建树和删除操作。

二叉查找树的创建

对于一棵二叉查找树，其创建与二叉树的创建很类似，略有不同的是，二叉查找树，为了保证整棵树都关于根结点的大小呈左小右大的特征，在创建时，需要根据当前结点的大小来判断插入位置，给出如下代码：

template<typename T>
void  BSTree<T>::createBSTreeByFile(ifstream &f){
    T e;
    queue<BSNode<T>*> q;
 
    while(!f.eof()){
        InputFromFile(f, e);
        Insert(root, e);
    }
}
 
template<typename T>
void BSTree<T>::Insert(BSNode<T>* &t, T x){//得用指针的引用，不然传参时由于形参实例化，并不能成功创建二叉树
 
    if(t==NULL){
        t = new BSNode<T>;
        t->data = x;
        t->lchild = t->rchild = NULL;
        return;
    }
 
    if(x<=t->data){
        Insert(t->lchild, x);
    }
    else{
        Insert(t->rchild, x);
    }
}

二叉查找树的查找

二叉查找树的查找有递归和非递归两种，对于递归方式，其递归边界为树的终止结点，非递归方式则采取对树中所有结点采取BFS或者DFS进行遍历的方式。

对于非递归方式，给出采取DFS的遍历方式，在这种方式中，通常采用入栈的方式，来访问每个结点，而根据访问的先后顺序，又分为，前序、中序和后序三种遍历方式。以前序遍历为例，通常以根、左、右的顺序访问遍历每个结点，而中序遍历方式，则以左、根、右的顺序遍历，后序则以左右根的顺序来访问。下面给出三种遍历方式的代码：前序遍历：

 template<typename T>
 void BSTree<T>::PreOrderTraverse(void(*visit)(BSNode<T>&))const{
     stack<BSNode<T>*> s;
     BSNode<T> *t = root;
     while(NULL!=t || !s.empty()){
         if(NULL!=t){
             s.push(t);
             visit(*t);
             t = t->lchild;
         }
         else{
             t = s.top();
             s.pop();
             t = t->rchild;
         }
     }
     cout<<endl;
 }

中序遍历：

 template<typename T>
 void BSTree<T>::InOrderTraverse(void(*visit)(BSNode<T>&))const{
     stack<BSNode<T>*> s;
     BSNode<T> *q;
 
     q = root;
 
     while(!s.empty()||q!=NULL){
         if(q!=NULL){
             s.push(q);
             q = q->lchild;
         }
         else{
             q = s.top();
             s.pop();
             visit(*q);
             q = q->rchild;
         }
     }
     cout<<endl;
 }

后序遍历，对于后序遍历，直接采用入栈的方式进行访问，是不行的，因为根结点被访问两次，无法保证你在弹栈后，对该结点如何操作，因此，需要另设置一个flag参数，来指明该节点是否左右子树都访问过，代码如下，我这里是令定义一个结构体，来实现：

/*结构体部分*/
enum Tags{Left, Right};
 
template<typename T>struct StackElem
{
    BSNode<T> *p;
    Tags flag;
};
 
/*后序遍历代码部分*/
template<typename T>
void BSTree<T>::PostOrderTraverse(void(*visit)(BSNode<T>&))const{
    StackElem<T> se;
    stack<StackElem<T> > s;
 
    BSNode<T> *t;
    t = root;
 
    if(t==NULL){
        return;
    }
    while(t!=NULL||!s.empty()){
        while(t!=NULL){
            se.flag = Left;
            se.p = t;
            s.push(se);
            t = t->lchild;
        }
        se = s.top();
        s.pop();
        t = se.p;
        if(se.flag==Left){
            se.flag = Right;
            s.push(se);
            t = t->rchild;
        }
        else{
            visit(*t);
            t = NULL;
        }
    }
}

以下是递归实现部分，递归实现，则是以二叉树边界为递归边界，前面已经说过了，其余逻辑与非递归一致，因为递归的过程，可以看作是一个入栈和弹栈的过程，即，在未到达边界时，通过递归，来访问下一个结点，例如左结点，当触及边界，则访问该结点，由于每次递归状态都被计算机保存，因此，在访问一个结点以后，返回上一个结点的状态，会依次访问上去。

递归前序遍历：

 template<typename T>
 void BSTree<T>::PreTraverse(BSNode<T> *t, void(*visit)(BSNode<T>&))const{
     if(t==NULL){
         return;
     }
     else{
         visit(*t);
         PreTraverse(t->lchild, visit);
         PreTraverse(t->rchild, visit);
     }
 }

递归中序遍历：

 template<typename T>
 void BSTree<T>::InTraverse(BSNode<T> *t, void(*visit)(BSNode<T>&))const{
     if(t==NULL){
         return;
     }
     else{
         InTraverse(t->lchild, visit);
         visit(*t);
         InTraverse(t->rchild, visit);
     }
 }

递归后序遍历：

 template<typename T>
 void BSTree<T>::PostTraverse(BSNode<T> *t, void(*visit)(BSNode<T>&))const{
     if(t!=NULL){
         PostTraverse(t->lchild, visit);
         PostTraverse(t->rchild, visit);
         visit(*t);
     }
 }

平衡二叉树（AVL树）

　　平衡二叉树是由前苏联的两位数学家G.M.Adelse-Velskil和E.M.Landis提出，因此一般也称作AVL树，AVL树本质还是一棵二叉查找树，只是在其基础上增加了“平衡”的要求。所谓平衡是指，对AVL树的任意结点来说，其左子树与右子树的高度之差的绝对值不超过1，其中左子树与右子树的高度因子之差称为平衡因子。

　　如下所示，就是一棵由{1，2，3，4，5，7，8}构建的AVL树：

　　

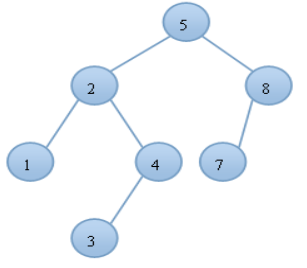
　　只要能随时保证每个结点平衡因子的绝对值不超过1，AVL的高度就始终能保持O(logn)级别，由于需要对每个结点都得到平衡因子，因此需要在树的结构中加入一个变量height来记录以当前结点为根结点的子树的高度。

AVL树的创建

　　AVL树的创建是基于二叉查找树的插入代码的基础上，增加平衡操作的。需要从插入的结点开始从下往上判断结点是否失衡，因此，需要在调用insert函数以后，更新当前子树的高度，并在这之后根据树型来进行相应的平衡操作。那么，怎么进行平衡操作呢？AVL树的插入是需要采取左旋或者右旋操作的，即，插入后，由于插入操作，导致某棵子树的高度超过了另一棵子树高度的2个结点高度，这样就破坏了树的平衡性，需要做出调整。

右旋操作

如下所示一棵简单的AVL树，对其进行插入操作以后：

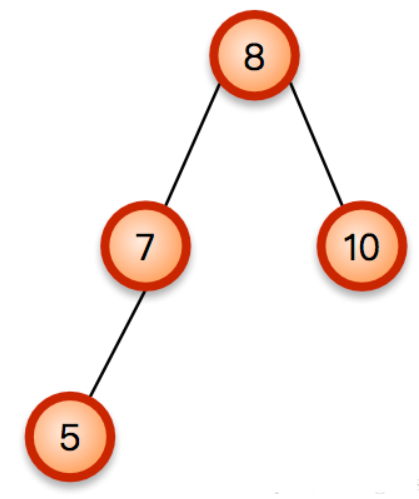
一棵简单的AVL树

变成了下图这样的AVL树：

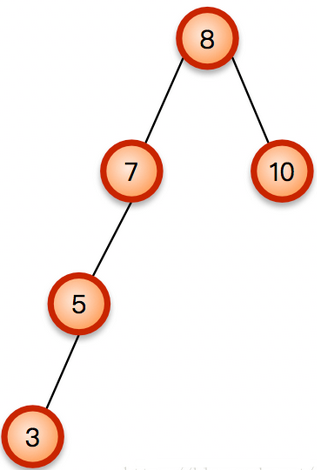
这样子就失衡了，所谓右旋操作，就是将这棵AVL树，从最靠近插入结点的失衡结点处，通过往右子树调整，使整棵树的每个结点的平衡因子变为正常，不如上图的树，离插入节点3最近的失衡结点是7，

则可以通过下图所示的操作，来平衡二叉树，即调整整棵树平衡因子：

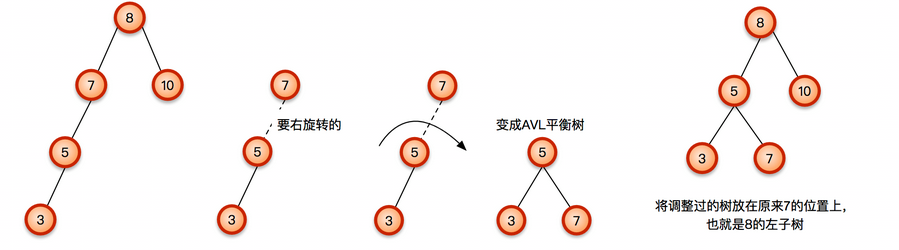
同样，左旋也与此类似。但是，如果5结点本身就有右结点，即如下所示：

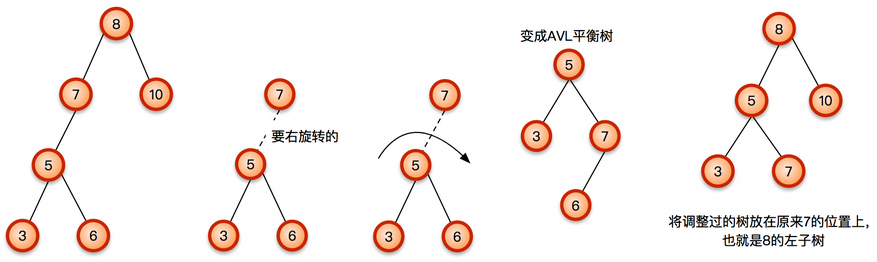
这样，在经过右旋操作以后，这棵树还是不平衡的，旋转后这棵树如下所示：

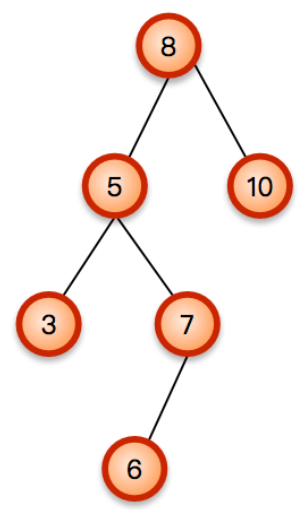
因此，还需要进行一次旋转，显然，继续右旋已经无法满足我们的需求，那么要如何进行操作，才能使这棵树回复平衡呢？（在后续中，会进行讲解）

左旋操作

左旋操作与右旋操作是类似的，都属于对子树的单旋转。

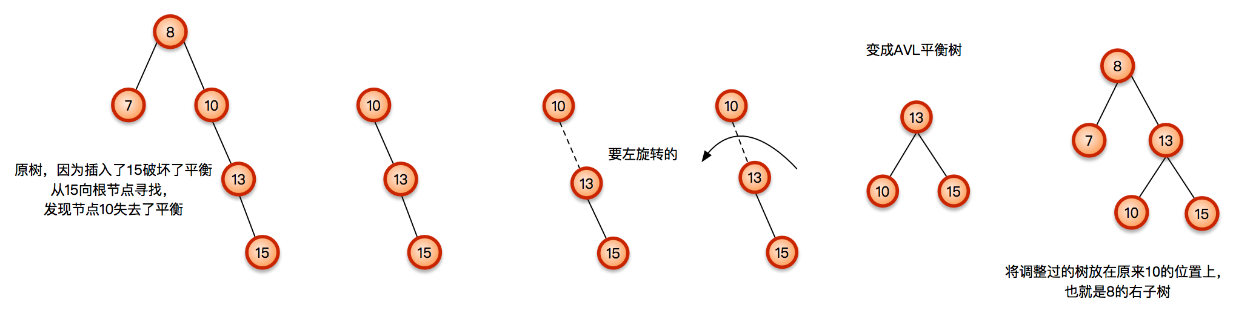
左旋与右旋一样，同样也存在这样的问题，如果该树的右子树的左结点存在，则单一通过左旋是做不到的，那么应该如何处理呢？

其实，以L和R来表示，插入结点的位置，有以下四种情况：

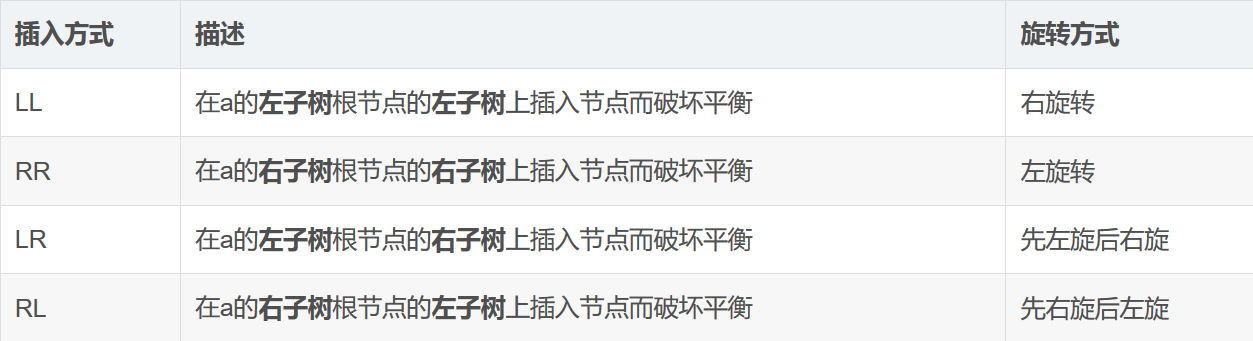
从上表可以看出，左旋和右旋两种情况中，左右结点若存在的话，就是上表中的RL和LR情况。则，只需要对两种情况分别按照上表采取相应的操作就可以解决，如下图所示：

LR型

RL型

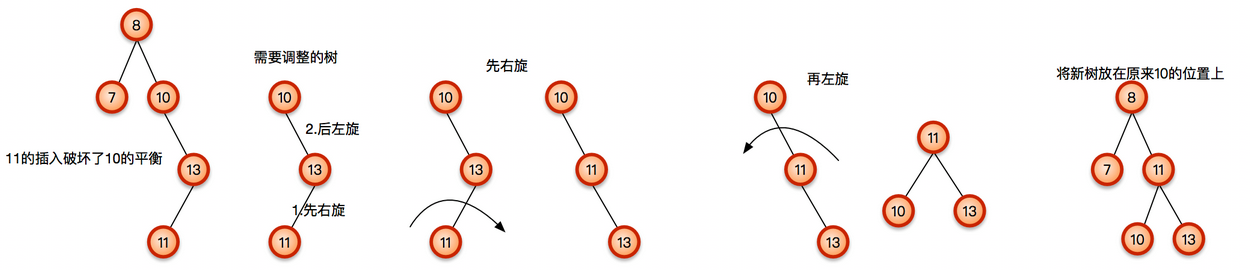
由此，就能实现AVL树的平衡，下面给出代码：

AVLTree.h

 #ifndef _AVLTREE_H_
 #define _AVLTREE_H_
 #include "C.h"
 #include "AVLNode.h"
 #include "Function.h"
 
 typedef int T;
 
 using namespace std;
 
 template<typename T>
 class AVLTree{
 private:
     AVLNode<T> *root;
     Destroy(AVLNode<T> *t){
         if(t!=NULL){
             Destroy(t->lchild);
             Destroy(t->rchild);
             delete t;
             t = NULL;
         }
         return ;
     }
 public:
     AVLTree(){
         root = NULL;
     }
     ~AVLTree(){
         Destroy(root);
     }
 
     AVLNode<T>* newAVLNode(T x);    //创建新结点
     void Insert(AVLNode<T>* &t, T x);
     void createAVLTreeFromFile(ifstream &f);
     AVLNode<T>* Root()const;
     int AVLTreeDepth(AVLNode<T> *t)const;
     int getAVLTreeHeight(AVLNode<T>* t)const;   //获取当前结点的高度
     int getBalanceFactor(AVLNode<T>* t)const;   //计算当前结点的高度
     void updateAVLNodeHeight(AVLNode<T>* &t);
     T getElem(AVLNode<T>* t)const;
     bool getElemExist(AVLNode<T>* &t)const;
     void LeftRotation(AVLNode<T>* &t);
     void RightRotation(AVLNode<T>* &t);
     void PreOrderTraverse(AVLNode<T>* t, void(*visit)(AVLNode<T>&))const;
     void PostOrderTraverse(AVLNode<T>* t, void(*visit)(AVLNode<T>&))const;
 };
 
 template<typename T>
 AVLNode<T>* AVLTree<T>::newAVLNode(T x){
     AVLNode<T>* avlnode = new AVLNode<T>;
     avlnode->data = x;
     avlnode->height = ;
     avlnode->lchild = avlnode->rchild = NULL;
     return avlnode;
 }
 
 template<typename T>
 void AVLTree<T>::Insert(AVLNode<T>* &t, T x){
     if(t==NULL){
         t = newAVLNode(x);
         return;
     }
     if(x==t->data){//结点已经存在，直接返回
         return;
     }
     if(x < t->data){
         Insert(t->lchild, x);
         updateAVLNodeHeight(t);
         if(getBalanceFactor(t)==){
             if(getBalanceFactor(t->lchild)==){
                 RightRotation(t);
             }
             else if(getBalanceFactor(t->lchild)==-){
                 LeftRotation(t->lchild);
                 RightRotation(t);
             }
         }
     }
     else{
         Insert(t->rchild, x);   //值比当前结点大，往右子树插入
         updateAVLNodeHeight(t);     //更新树高
         if(getBalanceFactor(t)==-){
             if(getBalanceFactor(t->rchild)==-){ //RR型
                 LeftRotation(t);
             }
             else if(getBalanceFactor(t->rchild)==){
                 RightRotation(t->rchild);
                 LeftRotation(t);
             }
         }
     }
 }
 
 template<typename T>
 void AVLTree<T>::createAVLTreeFromFile(ifstream &f){
     T e;
     while(!f.eof()){
         InputFromFile(f, e);
         Insert(root, e);
     }
 }
 
 template<typename T>
 AVLNode<T>* AVLTree<T>::Root()const{
     return root;
 }
 
 template<typename T>
 int AVLTree<T>::AVLTreeDepth(AVLNode<T> *t)const{
     int i,j;
     if(t==NULL){
         return ;
     }
     else{
         i = AVLTreeDepth(t->lchild);
         j = AVLTreeDepth(t->rchild);
     }
     return i>j ? i+ : j+;
 }
 
 template<typename T>
 int AVLTree<T>::getAVLTreeHeight(AVLNode<T>* t)const{
     if(t==NULL){
         return ;
     }
     return t->height;
 }
 
 template<typename T>
 int AVLTree<T>::getBalanceFactor(AVLNode<T>* t)const{
     if(t==NULL){
         return ;
     }
     return getAVLTreeHeight(t->lchild) - getAVLTreeHeight(t->rchild);
 }
 
 template<typename T>
 void AVLTree<T>::updateAVLNodeHeight(AVLNode<T>* &t){
     t->height = max(getAVLTreeHeight(t->lchild), getAVLTreeHeight(t->rchild)) + ;
 }
 
 template<typename T>
 T AVLTree<T>::getElem(AVLNode<T>* t)const{
     return t->data;
 }
 
 template<typename T>
 bool AVLTree<T>::getElemExist(AVLNode<T>* &t)const{//判断当前结点是否为空
     if(t!=NULL){
         return true;
     }
     return false;
 }
 
 template<typename T>
 void AVLTree<T>::LeftRotation(AVLNode<T>* &t){
     AVLNode<T> *temp = t->rchild;
     t->rchild = temp->lchild;
     temp->lchild = t;
     updateAVLNodeHeight(t);
     updateAVLNodeHeight(temp);
     t = temp;
 }
 
 template<typename T>
 void AVLTree<T>::RightRotation(AVLNode<T>* &t){
     AVLNode<T> *temp = t->lchild;
     t->lchild = temp->rchild;
     temp->rchild = t;
     updateAVLNodeHeight(t);
     updateAVLNodeHeight(temp);
     t = temp;
 }
 
 template<typename T>
 void AVLTree<T>::PreOrderTraverse(AVLNode<T>* t, void(*visit)(AVLNode<T>&))const{
     if(t!=NULL){
         visit(*t);
         PreOrderTraverse(t->lchild, visit);
         PreOrderTraverse(t->rchild, visit);
     }
 }
 
 template<typename T>
 void AVLTree<T>::PostOrderTraverse(AVLNode<T>* t, void(*visit)(AVLNode<T>&))const{
     if(t!=NULL){
         PostOrderTraverse(t->lchild, visit);
         PostOrderTraverse(t->rchild, visit);
         visit(*t);
     }
 }
 #endif // _AVLTREE_H_

Function.h

 #ifndef _FUNCTION_H_
 #define _FUNCTION_H_
 #include "C.h"
 #include "AVLNode.h"
 #include "AVLTree.h"
 
 typedef int T;
 
 using namespace std;
 
 bool InputFromFile(ifstream &f, T &e){
     f>>e;
     return f.good();
 }
 
 void visit(AVLNode<T> &t){
     cout<<t.data<<" ";
 }
 
 #endif // _FUNCTION_H_

C.h

 #ifndef _C_H_
 #define _C_H_
 #include<iostream>
 #include<string>
 #include<stdio.h>
 #include<algorithm>
 #include<map>
 #include<math.h>
 #include<queue>
 #include<stack>
 #include<vector>
 #include<fstream>
 #include<assert.h>
 #endif // _C_H_

AVLNode.h

 #ifndef _AVLNODE_H_
 #define _AVLNODE_H_
 
 typedef int T;
 
 template<typename T>
 struct AVLNode{
     int height;     //平衡因子
     T data;     //数据域
     AVLNode<T> *lchild, *rchild;    //指针域
 };
 #endif // _AVLNODE_H_