weblogic CVE-2018-2628漏洞利用工具
weblogic CVE-2018-2628漏洞利用
漏洞环境:
Windows2018R2
weblogic10.3.6
漏洞利用过程:
搭建好存在CVE-2018-2628漏洞的weblogic平台
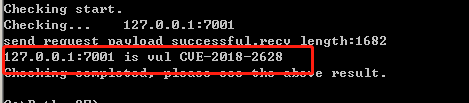
使用工具获得shell
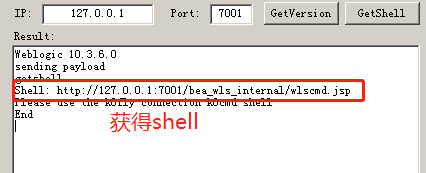
运行脚本,执行命令
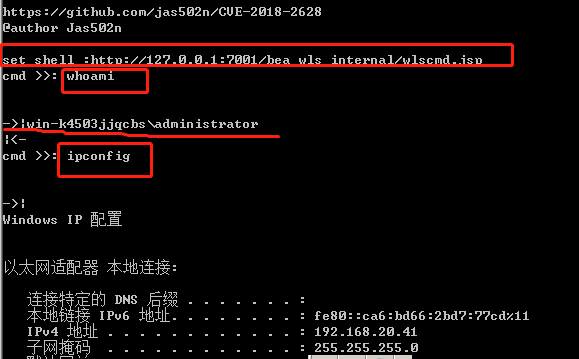
漏洞利用工具:
本文仅用于漏洞学习利用,禁止非法利用(后果自负)。
链接:https://pan.baidu.com/s/1VUSdwntnm4ViDTPgFSP6CA 密码:dto2
weblogic CVE-2018-2628漏洞利用工具的更多相关文章
- CVE-2014-6271 Bash漏洞利用工具
CVE-2014-6271 Bash漏洞利用工具 Exploit 1 (CVE-2014-6271) env x='() { :;}; echo vulnerable' bash -c "e ...
- 7. Vulnerability exploitation tools (漏洞利用工具 11个)
Metasploit于2004年发布时,将风暴带入了安全世界.它是开发,测试和使用漏洞利用代码的高级开源平台. 可以将有效载荷,编码器,无操作生成器和漏洞利用的可扩展模型集成在一起,使得Metaspl ...
- Struts2漏洞利用工具下载(更新2017-V1.8版增加S2-045/S2-046)
Struts2漏洞利用工具下载(已更新V1.8版) 2017-03-21:增加S2-046,官方发布S2-046和S2-045漏洞引发原因一样,只是利用漏洞的位置发生了变化,S2-046方式可能绕过部 ...
- [原创]K8 Struts2 Exp 20170310 S2-045(Struts2综合漏洞利用工具)
工具: K8 Struts2 Exploit组织: K8搞基大队[K8team]作者: K8拉登哥哥博客: http://qqhack8.blog.163.com发布: 2014/7/31 10:24 ...
- WebDAV服务漏洞利用工具DAVTest
WebDAV服务漏洞利用工具DAVTest WebDAV是基于Web服务的扩展服务.它允许用户像操作本地文件一样,操作服务器上的文件.借助该功能,用户很方便的在网络上存储自己的文件.为了方便用户使 ...
- ASP.net 资源请求漏洞利用工具PadBuster
ASP.net 资源请求漏洞利用工具PadBuster 在ASP.net 网站中,为了便于部署网站项目,开发者往往会将资源(图片.Javascript文件)嵌入到dll文件中.而网页中,会使用WebR ...
- 路由器漏洞利用工具RouterSploit
路由器漏洞利用工具RouterSploit 网络中存在大量的嵌入式设备,如路由器.智能摄像头.这类设备安全防护程度较低.由于这些设备更新不方便,一旦发现漏洞,往往不能及时修复.所以,在网络渗透测试中 ...
- 利用NSA的MS17-010漏洞利用工具实现Win 7和Win Server 2008系统入侵
影子经纪人(Shadow Brokers)最近陆续曝光的NSA网络武器令人震惊,尽管这些工具是否出自国家级别黑客团队之手尚不清楚,但至少存在一个可以说明问题的事实:这些漏洞利用工具都能有效运行,且具有 ...
- CVE-2017-3248——WebLogic反序列化漏洞利用工具
著名的web中间件WebLogic被曝出之前的反序列化安全漏洞补丁存在绕过安全风险,用户更新补丁后,仍然存在被绕过成功执行远程命令攻击的情况,安全风险高,Oracle官方及时发布了最新补丁,修复了该漏 ...
随机推荐
- Neo4j使用Cypher查询图形数据
Neo4j使用Cypher查询图形数据,Cypher是描述性的图形查询语言,语法简单,功能强大,由于Neo4j在图形数据库家族中处于绝对领先的地位,拥有众多的用户基数,使得Cypher成为图形查询语言 ...
- Mysql 用户权限管理
1. MySQL 权限介绍 mysql中存在4个控制权限的表,分别为user表,db表,tables_priv表,columns_priv表,我当前的版本mysql 5.7.22 . mysql权限表 ...
- go import使用及. _的作用解析
go中import用于导入包.导入之后就可以使用包中的代码. 比如: import( "fmt" ) 在代码中就可以使用fmt包中的方法,如: fmt.Println(" ...
- Spring的第三天AOP之xml版
Spring的第三天AOP之xml版 ssm框架 spring AOP介绍 AOP(Aspect Oriented Programming),面向切面编程.它出来的目的并不是去取代oop,而是对它的 ...
- [EZOJ1007] 神奇的三角形
Description 求 \(\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{i}C(i,j)\times (j+1)^m\operatorname{mod}99 ...
- Mybatis之基于XML的调用存储过程与手动回滚事务
一.调用存储过程 一.返回单个值 1.存储过程准备 这里先创建一个存储过程,传入参数为age,传出参数为count.然后先测试一下是否正确. CREATE DEFINER=`root`@`localh ...
- Fibonacci快速实现(优化)
斐波那契数列的通俗解法是利用递推公式进行递归求解,我们可以更优化的去解决它. 方法一:通项公式 斐波那契数列的递推公式是f(n)=f(n-1)+f(n-2),特征方程为:x2=x+1,解该方程得(1+ ...
- 【转】 Apk文件及其编译过程
Apk文件概述 Android系统中的应用程序安装包都是以apk为后缀名,其实apk是Android Package的缩写,即android安装包. 注:apk包文件其实就是标准的zip文件,可以直接 ...
- 【手记】VSTO部署中的坑
局域网部署,客户机安装时报[部署清单签名的证书或其位置不受信任]: 在[Internet 属性]里(可运行inetcpl.cpl打开),把服务器内网IP加进[受信任站点]就好,不用管excel信任中心 ...
- IdentityServer4-Resource定义-翻译
资源定义(Defining Resource) 通常,第一件事是定义那些你想保护的资源.这些资源可能是你的用户信息,比如个人数据,电子邮件或者对Api的访问. Note: 你可以用C#实体类来定义资源 ...
