【Static Program Analysis - Chapter 4】格理论(Lattice Theory)与程序分析

# 从一个例子说起，

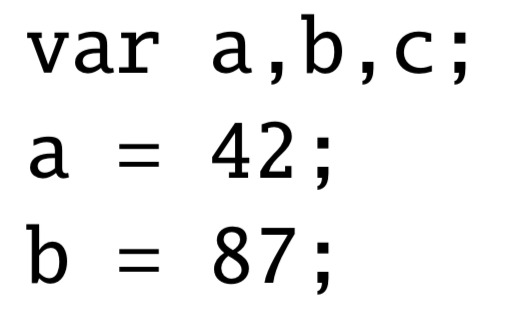
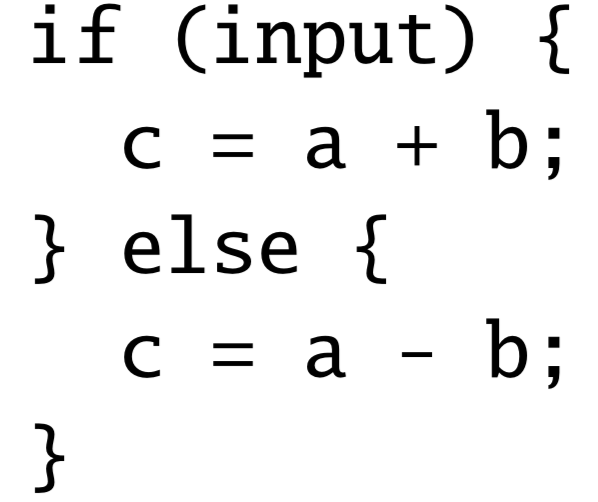
**任务：给定这样一段代码，假设我们想分析出这段代码中，每个数值型变量和表达式的符号，即正数，负数或0。**

此外，还有可能出现两种情况就是：

1.我们无法分析出结果，即我们无法确定符号，用(?)表示；

2.有些表达式的值并不是一个数字（例如，有可能是个指针）或者在执行的过程中没有被赋值（有可能是因为对于给定的输入，没有执行到，unreachable），用(⊥)表示。

因此，对于每一个变量或者是表达式，我们会有5种结果(这里将其表征成“格”的形式)：

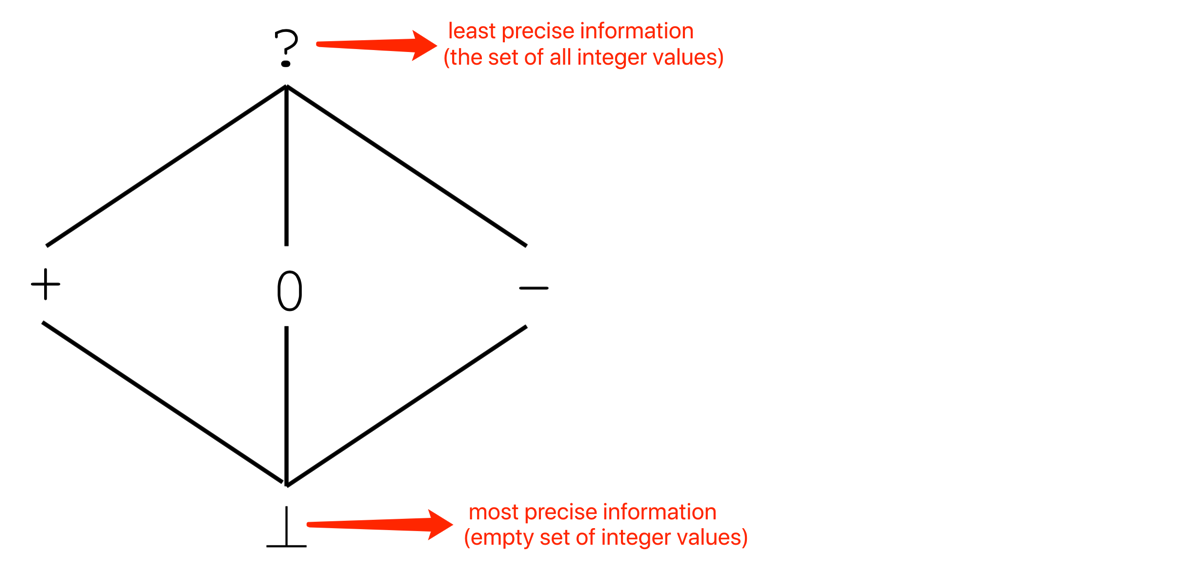
(?)可能的原因是：

1.执行多次，变量c是正数或者是负数的结果都出现过。所以标记为(?)更加保险；

2.分析方法无法证明结果的确定性。如，执行多次变量都是正数，但是分析方法无法证明变量一定是正数。

 # 格理论(Lattice Theory)

## 偏序集合(Partially ordered set，简写poset)

首先了解一个概念叫*偏序集合*，（英语：Partially ordered set，简写poset）是数学中，特别是序理论中，指配备了部分排序关系的集合。 这个理论将排序、顺序或排列这个集合的元素的直觉概念抽象化。这种排序不必然需要是全部的，就是说不必要保证此集合内的所有对象的相互可比较性。部分排序集合定义了部分排拓扑。（更多详细的介绍见维基百科）

理解偏序 & 全序:

偏序：集合内只有部分元素之间在这个关系下是可以比较的。
比如：比如复数集中并不是所有的数都可以比较大小，那么“大小”就是复数集的一个偏序关系。 

全序：集合内任何一对元素在在这个关系下都是相互可比较的。
比如：有限长度的序列按字典序是全序的。最常见的是单词在字典中是全序的。

 

偏序关系即给定集合S，“≤”是S上的二元关系，若“≤”满足：

1. 自反性：∀a∈S，有a≤a；
2. 反对称性：∀a，b∈S，a≤b且b≤a，则a=b；
3. 传递性：∀a，b，c∈S，a≤b且b≤c，则a≤c；

则称“≤”是S上的非严格偏序或自反偏序。

 

全序关系即集合X上的反对称的、传递的和完全的二元关系（一般称其为≤）。

若X满足全序关系，则下列陈述对于X中的所有a, b和c成立：

• 反对称性：若a ≤ b且b ≤ a则a = b
• 传递性：若a ≤ b且b ≤ c则a ≤ c
• 完全性：a ≤ b或b ≤ a

 

注意：完全性(全序)本身也包括了自反性。
所以，全序关系必是偏序关系。

 

## 格，a lattice is a pair(S,⊑) 

在数学中，格是其非空有限子集都有一个上确界（叫并）和一个下确界（叫交）的偏序集合（poset）。格也可以特征化为满足特定公理恒等式的代数结构。因为两个定义是等价的，格理论从序理论和泛代数二者提取内容。半格包括了格，依次包括海廷代数和布尔代数。这些"格样式"的结构都允许序理论和抽象代数的描述。（更多详细的介绍见维基百科）

 

序理论定义

 考虑任意一个偏序集合（L,≤），如果对集合L中的任意元素a,b，使得a,b在L中存在一个最大下界，和最小上界，则(L,≤)是一个格。

这里对于取a,b的最大下界的操作用{\displaystyle a\wedge b}表示；

对于取a,b的最小上界操作用 {\displaystyle a\vee b}表示。

有界格有一个最大元素和一个最小元素，按惯例分别指示为1和0（也叫做顶和底）。任何格都可以通过增加一个最大元素和最小元素而转换成有界格。

 

使用容易的归纳论证，你可以演绎出任何格的所有非空有限子集的上确界（并）和下确界（交）的存在。一个很重要的格的种类是完全格。一个格是完全的，如果它的所有子集都有一个交和一个并，这对比于上述格的定义，这里只要求所有非空有限子集的交和并的存在。

例子：

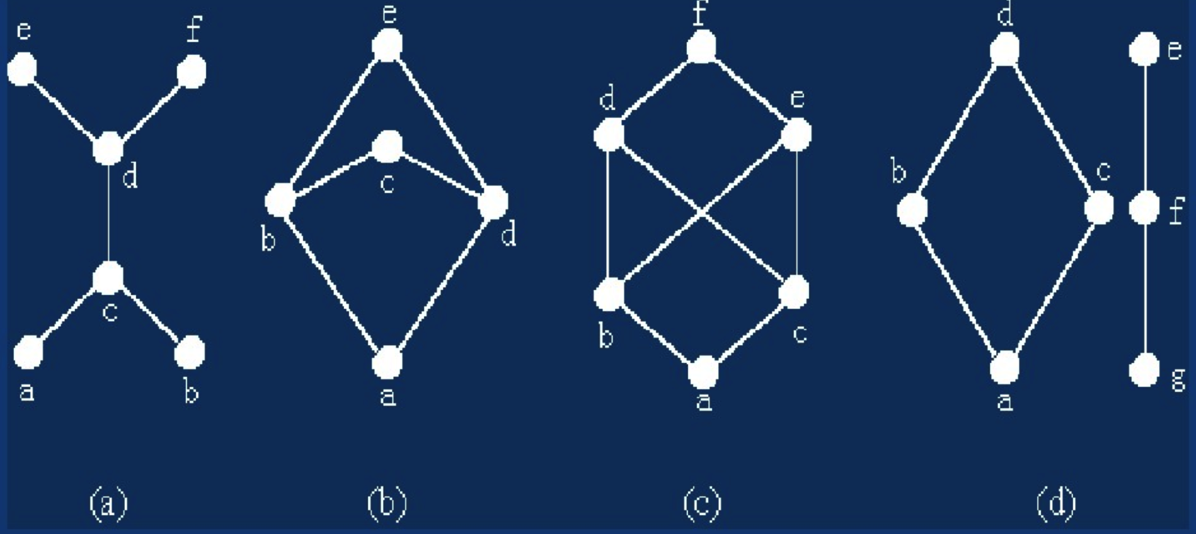
任何一个有限的偏序集合可以表示成一张哈斯图（Hasse diagram，每个元素代表一个节点，顺序关系是边的传递闭包，由低到高），如，

 

以上都是格，以下都不是格：

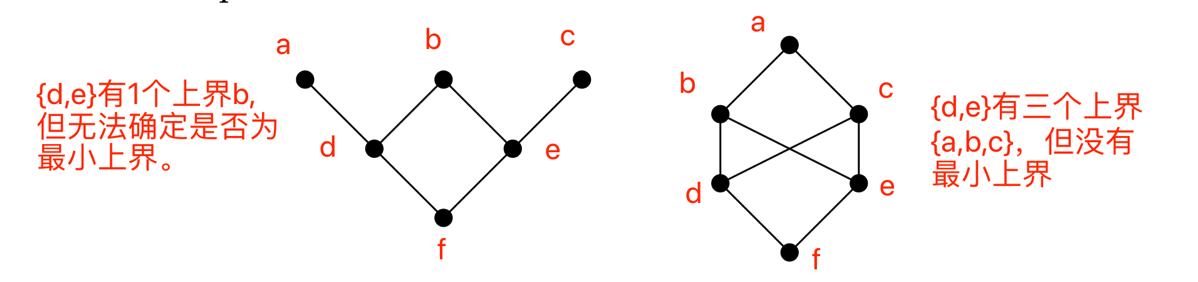
其他一些例子：

 

## 不动点(fixed-points)

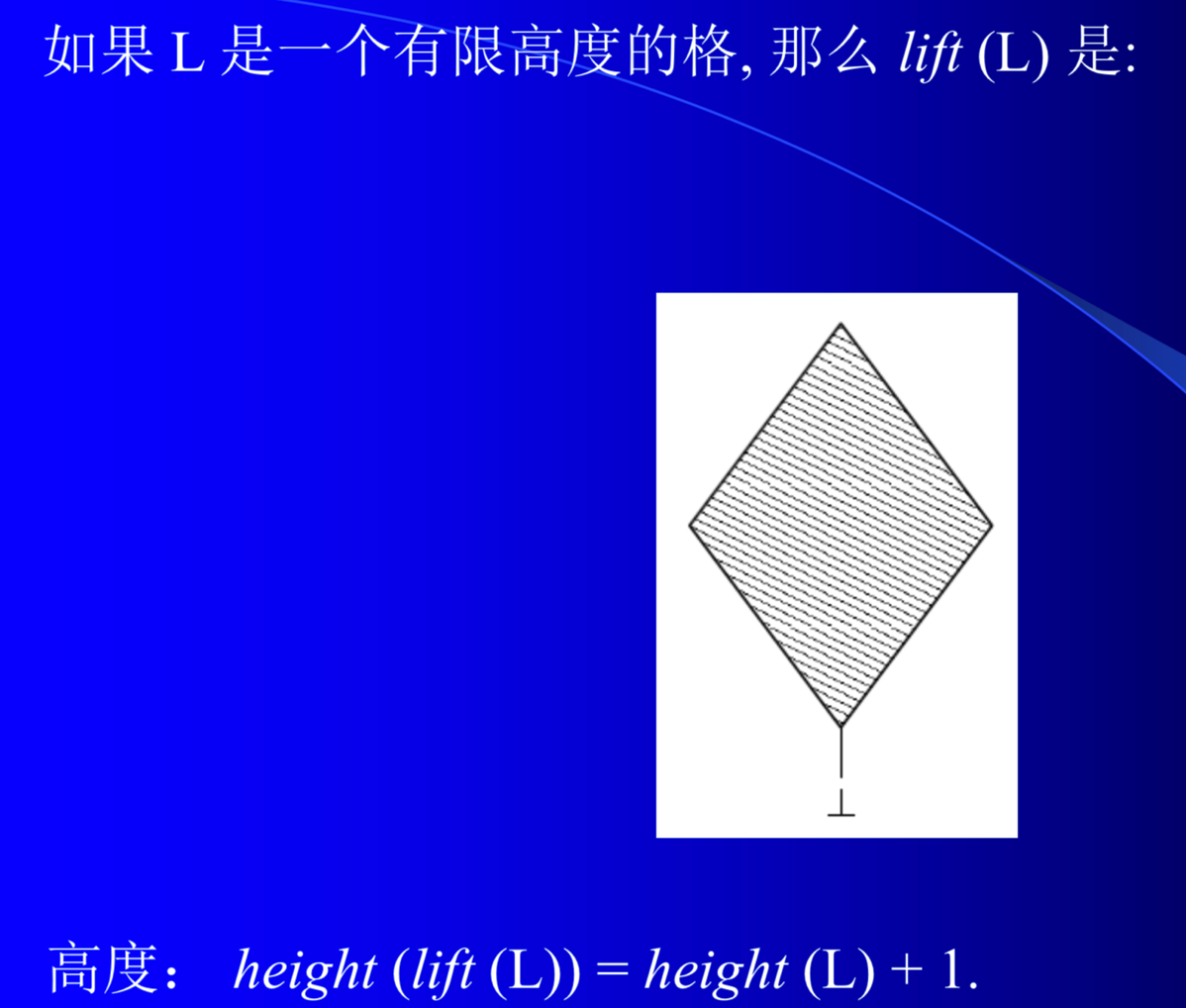
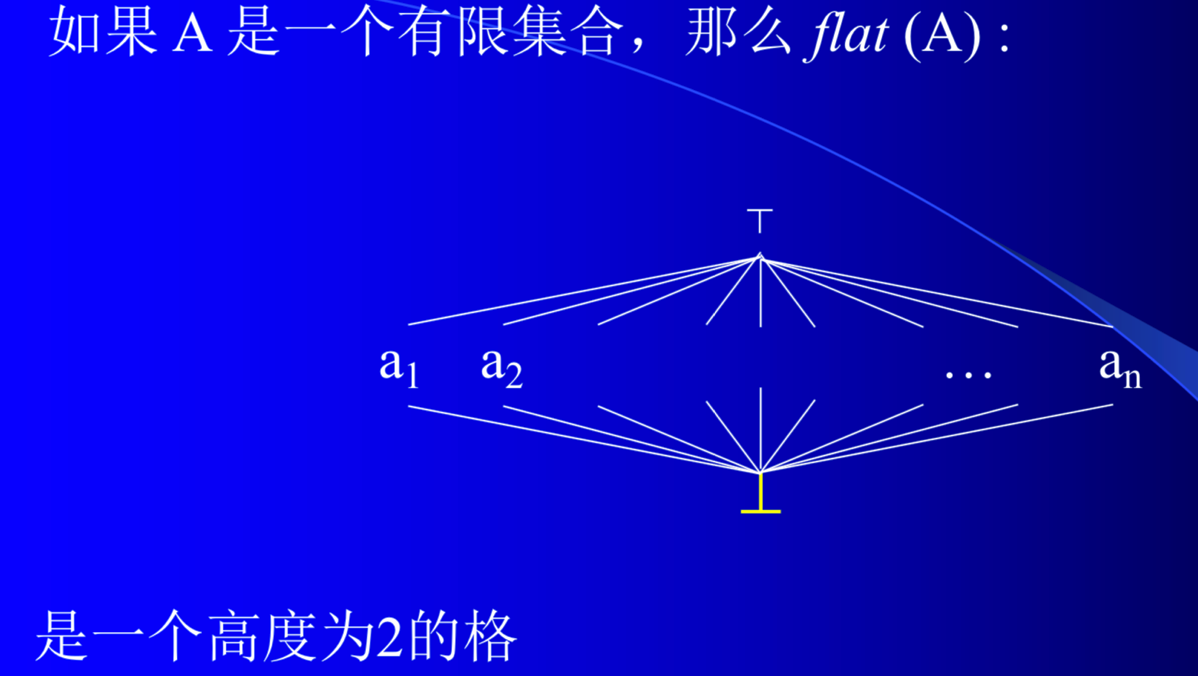
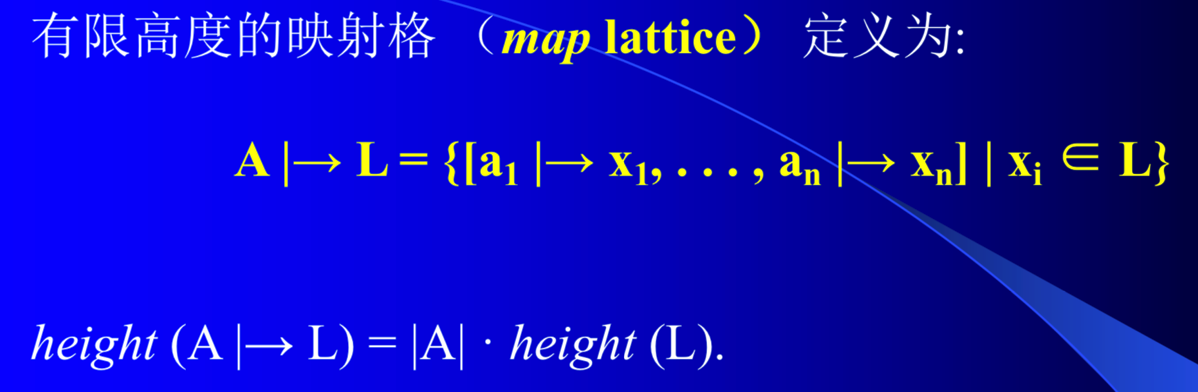
这里引用王千祥老师的slide作为补充: