Followme Devops实践之路

引言

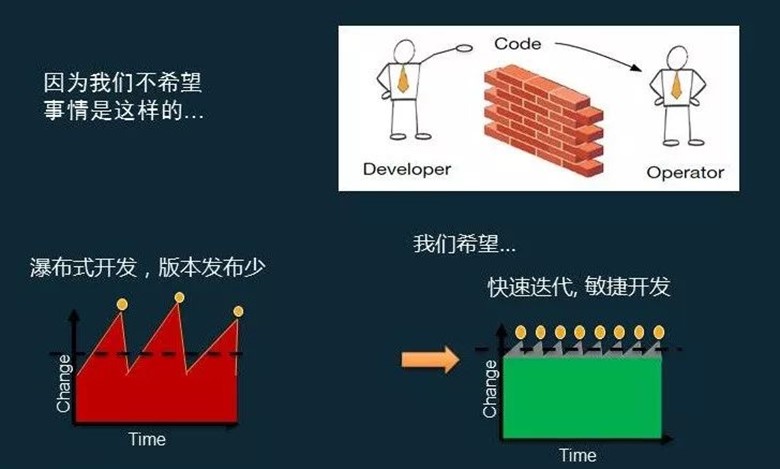
天下武功,唯快不破

想要提高开发团队效率，势必要有一套完整而成熟的开发流程方案，除了sprint迭代开发模式之外,还有近几年流行的devops流程,都是可以大幅度提高开发效率的工具. 我们团队也不断探索、实践，最终形成了现有的一套体系，从最初的手动发布到现有的自动化，从起始的繁琐易乱到当下的简洁明了。我们希望将我们曾经踏过的脚印与大家一起分享，为各位展示一条 我们的devops 的实践之路，同时也希望能为各位避免走入同样的弯路提供些许帮助。

 

背景

我们是一个 .net(core) / go / nodejs 的多语言混合式开发团队，致力于微服务架构。项目初期基于 .net framework, 开始并没有准备做 devops，基于Windows的 gRPC 服务、ASP.NET 做持续部署还是比较麻烦（不管是停止远程服务/更新二进制包/docker化流程都太重）。当我们全面拥抱.net core 2.0之后，其原生跨平台的特性促成了我们的 CI/CD (continue integration/continue deployment) 之路。

 

发展历程

从0,到devops我们也经历过好几个阶段,每个阶段所存在的问题, 大家也可以对号入座的看看

1 原始阶段/纯人工管控

• 大家司空见惯的在开发机build,然后copy到服务器上,手工解压更新,启动服务!
• 这种方式效率太低, 质量也不敢保证, 没有流程章法

2 Ansible + git

• 采用git来管理二进制发布包 ,可以有效的进行发布的粗略diff/特别是配置文件
• 采用ansible来管理服务器,大大减低了人肉成本
• 运维大量的重复性操作

3. devops

 

Devops

为了实现开发自运维, 我们采用Jenkins +docker + portainer 三剑客, 来解决开发/运维/服务器/各自的问题

1. Docker
   1. 环境依赖, 例如 .net core runtime版本/ OS 版本, 再也不用让运维提前准备环境了
   2. 资源限制, 例如有些服务存在内存泄漏/CPU问题, docker可以限制他的最大使用率, 确保同台服务器上其他docker 服务可以正常使用
2. Portainer
   1. Docker management UI
   2. 统一管理docker服务
3. Jenkins
   1. Build source code
   2. Build docker image ,ship
   3. Auto deploy

架构如下 https://github.com/FollowmeTech/jenkins-cicd

功能

• base on Jenkins
• base on docker register hub
• base on portainer management

依赖

• docker registry [harbor]
• portainer (docker management)
• git-server
• docker /docker-compose

体验一下

为了方便大家快熟感受, 我搭建了一个play环境

大家可以向 https://github.com/FollowmeTech/jenkins-cicd-practise 提交代码

再登陆 https://ci.rileme.club ,选择相应的分支进行build发布 (play/123456)

项目发布完成, 快熟预览效果 http://demo.rileme.club

部署使用

广告时间

Hi, 是的,我们在招聘 , 详情如下

https://github.com/FollowmeTech/hire/blob/master/dotnet.md

你是想一辈子卖糖水, 还是再折腾折腾

Think about it