一致性哈希（附带C++实现）

　　在分布式集群中，对机器的添加删除，或者机器故障后自动脱离集群这些操作是分布式集群管理最基本的功能。如果采用常用的hash(object)%N算 法，那么在有机器添加或者删除后，就需要大范围的移动原有数据，这种大规模的移动数据在大规模的分布式集群中是不可被接受的，因为移动过程中造成的‘抖动’或者可能出现的数据读写问题，都会大大降低集群的可用性。谷歌前一段（17年4月）时间对一致性哈希做了简单改进，即对每个节点最大连接数做限制，新来的请求如果发现目标节点达到最大限制，就会顺时针方向寻找下一个连接数没达到最大的节点，相关论文如下

Consistent Hashing with Bounded Loads

Monday, April 03, 2017

Posted by Vahab Mirrokni, Principal Scientist, Morteza Zadimoghaddam, Research Scientist, NYC Algorithms Team

Running a large-scale web service, such as content hosting, necessarily requires load balancing — distributing clients uniformly across multiple servers such that none get overloaded. Further, it is desirable to find an allocation that does not change very much over time in a dynamic environment in which both clients and servers can be added or removed at any time. In other words, we need the allocation of clients to servers to be consistent over time.

In collaboration with Mikkel Thorup, a visiting researcher from university of Copenhagen, we developed a new efficient allocation algorithm for this problem with tight guarantees on the maximum load of each server, and studied it theoretically and empirically. We then worked with our Cloud team to implement it in Google Cloud Pub/Sub, a scalable event streaming service, and observed substantial improvement on uniformity of the load allocation (in terms of the maximum load assigned to servers) while maintaining consistency and stability objectives. In August 2016 we described our algorithm in the paper “Consistent Hashing with Bounded Loads”, and shared it on ArXiv for potential use by the broader research community.

Three months later, Andrew Rodland from Vimeo informed us that he had found the paper, implemented it in haproxy (a widely-used piece of open source software), and used it for their load balancing project at Vimeo. The results were dramatic: applying these algorithmic ideas helped them decrease the cache bandwidth by a factor of almost 8, eliminating a scaling bottleneck. He recently summarized this story in a blog post detailing his use case. Needless to say, we were excited to learn that our theoretical research was not only put into application, but also that it was useful and open-sourced.

Background

While the concept of consistent hashing has been developed in the past to deal with load balancing in dynamic environments, a fundamental issue with all the previously developed schemes is that, in certain scenarios, they may result in sub-optimal load balancing on many servers.

Additionally, both clients and servers may be added or removed periodically, and with such changes, we do not want to move too many clients. Thus, while the dynamic allocation algorithm has to always ensure a proper load balancing, it should also aim to minimize the number of clients moved after each change to the system. Such allocation problems become even more challenging when we face hard constraints on the capacity of each server - that is, each server has a capacity that the load may not exceed. Typically, we want capacities close to the average loads.

In other words, we want to simultaneously achieve both uniformity and consistency in the resulting allocations. There is a vast amount of literature on solutions in the much simpler case where the set of servers is fixed and only the client set is updated, but in this post we discuss solutions that are relevant in the fully dynamic case where both clients and servers can be added and removed.

 

The Algorithm

We can think about the servers as bins and clients as balls to have a similar notation with well-studied balls-to-bins stochastic processes. The uniformity objective encourages all bins to have a load roughly equal to the average density (the number of balls divided by the number of bins). For some parameter ε, we set the capacity of each bin to either floor or ceiling of the average load times (1+ε). This extra capacity allows us to design an allocation algorithm that meets the consistency objective in addition to the uniformity property.

Imagine a given range of numbers overlaid on a circle. We apply a hash function to balls and a separate hash function to bins to obtain numbers in that range that correspond to positions on that circle. We then start allocating balls in a specific order independent of their hash values (let’s say based on their ID). Then each ball is moved clockwise and is assigned to the first bin with spare capacity.

Consider the example above where 6 balls and 3 bins are assigned using two separate hash functions to random locations on the circle. For the sake of this instance, assume the capacity of each bin is set to 2. We start allocating balls in the increasing order of their ID values. Ball number 1 moves clockwise, and goes to bin C. Ball number 2 goes to A. Balls 3 and 4 go to bin B. Ball number 5 goes to bin C. Then ball number 6 moves clockwise and hits bin B first. However bin B has capacity 2 and already contains balls 3 and 4. So ball 6 keeps moving to reach bin C but that bin is also full. Finally, ball 6 ends up in bin A that has a spare slot for it.

Upon any update in the system (ball or bin insertion/deletion), the allocation is recomputed to keep the uniformity objective. The art of the analysis is to show that a small update (a few number of insertions and deletions) results in minor changes in the state of the allocation and therefore the consistency objective is met. In our paper we show that every ball removal or insertion in the system results in O(1/ε2) movements of other balls. The most important thing about this upper bound is that it is independent of the total number of balls or bins in the system. So if the number of balls or bins are doubled, this bound will not change. Having an upper bound independent of the number of balls or bins introduces room for scalability as the consistency objective is not violated if we move to bigger instances. Simulations for the number of movements (relocations) per update is shown below when an update occurs on a bin/server.

The red curve shows the average number of movements and the blue bars indicate the variance for different values of ε (the x-axis). The dashed curve is the upper bound suggested by our theoretical results which fits nicely as a prediction of the actual number of movements. Furthermore, for any value of ε, we know the load of each bin is at most (1+ε) times the average load. Below we see the load distribution of bins for different values of ε=0.1, ε=0.3 and ε=0.9.

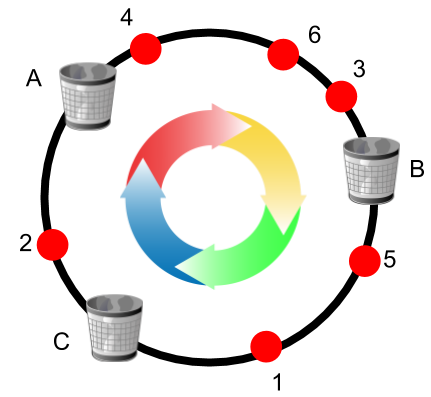
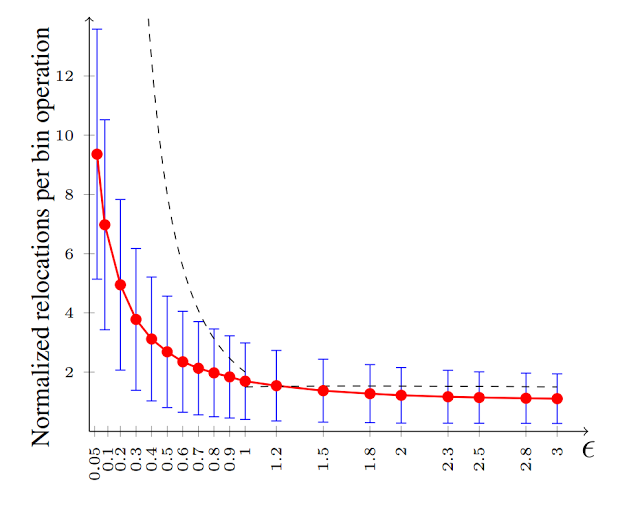
The distribution of loads for several values of ε. The load distribution is nearly uniform covering all ranges of loads from 0 to (1+ε) times average, and many bins with load equal to (1+ε) times average.

As one can see there is a tradeoff — a lower ε helps with uniformity but not with consistency, while larger ε values help with consistency. A lower ε will ensure that many loads will be equal to the hard capacity limit of (1+ε) times the average, and the rest have a decaying distribution.

When providing content hosting services, one must be ready to face a variety of instances with different characteristics. This consistent hashing scheme is ideal for such scenarios as it performs well even for worst-case instances.

While our internal results are exciting, we are even more pleased that the broader community found our solution useful enough to open-source, allowing anyone to use this algorithm. If you are interested in further details of this research, please see the paper on ArXiv, and stay tuned for more research from the NYC Algorithms Team!

Acknowledgements:

We would like to thank Alex Totok, Matt Gruskin, Sergey Kondratyev and Haakon Ringberg from the Google Cloud Pub/Sub team, and of course Mikkel Thorup for his invaluable contributions to this paper.

 

　　下面用C++实现了一个简单的一致性哈希代码：

#include <iostream>
#include <algorithm>
#include <fstream>
#include <vector>
#include <map>
#include <list>
#include <random>

#include <sys/socket.h>
#include <netinet/in.h>
#include <arpa/inet.h>

/*
 * ===  FUNCTION  ======================================================================
 *         Name:  add_key
 *  Description:  找出ip地址对应的node，并存储到node对应的ip列表
 * =====================================================================================
 */
void add_key(const std::map<uint32_t, std::string> &node_info, std::string ip, std::map<uint32_t, std::vector<uint32_t>> &info)
{
	if (ip.empty() || node_info.empty())
		return;

	/* key映射的hash函数（简单的对ip地址取模） */
	auto value = inet_addr(ip.c_str());
	auto hash_value = value % 16384;

	auto it = node_info.begin();
	auto right_value = it->first;
	uint32_t left_value = right_value;
	while (it != node_info.end()) {
		left_value = right_value;
		right_value = it->first;

		/* 如果当前key在最小的node左边或者两个node之间就进行处理 */
		if (hash_value <= left_value || hash_value <= right_value) {
			/* 查看key要访问的node是否存在与映射表中 */
			auto itr = info.find(right_value);
			if (itr == info.end()) {
				std::vector<uint32_t> cli;
				cli.push_back(value);
				info.emplace(right_value, cli);
			}
			else {
				itr->second.push_back(value);
			}
			break;
		}

		it++;
	}

	/* 由于是环形0-16383范围，所以当没有找到比当前key大的node，就需要绕回，将其映射到node值最小的node上 */
	if (it == node_info.end()) {
		auto itr = info.find(node_info.begin()->first);
		if (itr == info.end()) {
			std::vector<uint32_t> cli;
			cli.push_back(value);
			info.emplace(right_value, cli);
		}
		else {
			itr->second.push_back(value);
		}
	}
}

/*
 * ===  FUNCTION  ======================================================================
 *         Name:  del_key
 *  Description:  删除node映射表中的key
 * =====================================================================================
 */
bool del_key(std::map<uint32_t, std::vector<uint32_t>> &info, const std::string &ip)
{
	if (ip.empty() || info.empty())
		return false;

	/* hash函数取值 */
	auto value = inet_addr(ip.c_str());
	uint32_t hash_value = value % 16384;

	auto it = info.begin();
	auto right_value = it->first;
	uint32_t left_value = right_value;
	while (it != info.end()) {
		left_value = right_value;
		right_value = it->first;

		if (hash_value <= left_value || hash_value <= right_value) {
			auto target = std::find(it->second.begin(), it->second.end(), hash_value);
			if (target != it->second.end())
				it->second.erase(target);
			std::cout << "delete " << ip << " from node " << right_value << std::endl;

			break;
		}

		it++;
	}

	if (it == info.end()) {
		it = info.begin();
		auto target = std::find(it->second.begin(), it->second.end(), hash_value);
		if (target != it->second.end())
			it->second.erase(target);
		std::cout << "delete " << ip << " from node " << right_value << std::endl;
	}

}

/*
 * ===  FUNCTION  ======================================================================
 *         Name:  add_node
 *  Description:  node列表中新增一个node，如果原有node映射表中有数据的话需要将新加node
 *  			  之前范围内的key数据从node后面的node映射表中迁移到新加node中
 * =====================================================================================
 */
bool add_node(std::map<uint32_t, std::string> &node_info, std::map<uint32_t, std::vector<uint32_t>> &info, const std::string &node_name)
{
	/* 验证node_name是否已经存在 */
	for (const auto &ele : node_info) {
		if (ele.second == node_name)
			return false;
	}

	/* c++11 provides random class */
	std::random_device rd;
	std::mt19937 gen(rd());
	/* 获取0-16383范围内的随机数 */
	std::uniform_int_distribution<> dis(0, 16383);

	/* 利用随机数来作为hash函数 */
	auto node_key = dis(gen);
	node_info.emplace(node_key, node_name);

	std::vector<uint32_t> cli;

	if (info.empty())
		return true;

	auto it = info.begin();
	auto right_value = it->first;
	uint32_t left_value = right_value;
	while (it != info.end()) {
		left_value = right_value;
		right_value = it->first;

		if (node_key < left_value || node_key < right_value) {
			if (it->second.empty())
				return true;

			/* 如果新node要插入的区间中有数据，需要进行数据迁移 */
			auto ip_arr = it->second;
			for (auto itr = ip_arr.begin(); itr != ip_arr.end(); itr++) {
				if (*itr > node_key && *itr <= right_value)
					continue;

				cli.push_back(*itr);
				itr = ip_arr.erase(itr);
			}
			break;
		}

		it++;
	}

	info.emplace(node_key, cli);

	return true;
}

/*
 * ===  FUNCTION  ======================================================================
 *         Name:  del_node
 *  Description:  将node删除，如果node上有映射数据，需要将数据迁移到顺时针方向上的下一个
 * =====================================================================================
 */
bool del_node(std::map<uint32_t, std::string> &node_info, std::map<uint32_t, std::vector<uint32_t>> &info, const std::string &node_name)
{
	auto key_itr = node_info.begin();
	while (key_itr->second != node_name)
		key_itr++;

	if (key_itr == node_info.end())
		return false;

	if (info.empty()) {
		node_info.erase(key_itr);
		return true;
	}

	auto target = info.find(key_itr->first);
	if (target == info.end()) {
		node_info.erase(key_itr);
		return true;
	}

	/* 如果删除的是最后一个node，则将数据迁移到第一个node上 */
	target++;                                   /* 因为map的迭代器不是随机迭代器，因此只能用++或者--，而不能用+、- */
	if (target == info.end()) {
		target--;
		auto &ip_arr = info.begin()->second;
		ip_arr.insert(ip_arr.end(), target->second.begin(), target->second.end());
	}
	else {
		auto &ip_arr = target->second;
		target--;
		ip_arr.insert(ip_arr.end(), target->second.begin(), target->second.end());
	}
	info.erase(target);

	node_info.erase(key_itr);

	return true;
}

int main(int argc, char *argv[])
{
	std::vector<std::string> addrs = {"192.168.54.1#1", "192.168.54.1#2","192.168.54.1#3","192.168.54.2#1","192.168.54.2#2","192.168.54.2#3","192.168.54.3#1","192.168.54.3#2","192.168.54.3#3"};

	std::cout << "convert 192.168.1.1 to long is " << inet_addr("192.168.1.1") % 16384 << std::endl;

	std::map<uint32_t, std::string> nodes;
	std::map<uint32_t, std::vector<uint32_t>> info;
	for (const auto & ele : addrs) {
		add_node(nodes, info, ele);
	}

	std::string ip;
	std::ifstream ifs;
	ifs.open("conf");

	while (!ifs.eof()) {
		ifs >> ip;
		if (ip.empty())
			break;
		std::cout << "Get ip addr " << ip << std::endl;
		add_key(nodes, ip, info);
		ip.clear();
	}

	del_node(nodes, info, "192.168.54.1#2");
	del_key(info, "100.64.6.225");

	return EXIT_SUCCESS;
}				/* ----------  end of function main  ---------- */