SDN第一次上机作业

作业链接

• 用字符命令生成拓扑，并测试连通性，截图

  sudo mn --topo tree,fanout=3,depth=2

  

• 用可视化界面生成拓扑，并测试连通性，截图
  
  

• 用Python脚本生成一个Fat-tree型的拓扑，截图
  
  

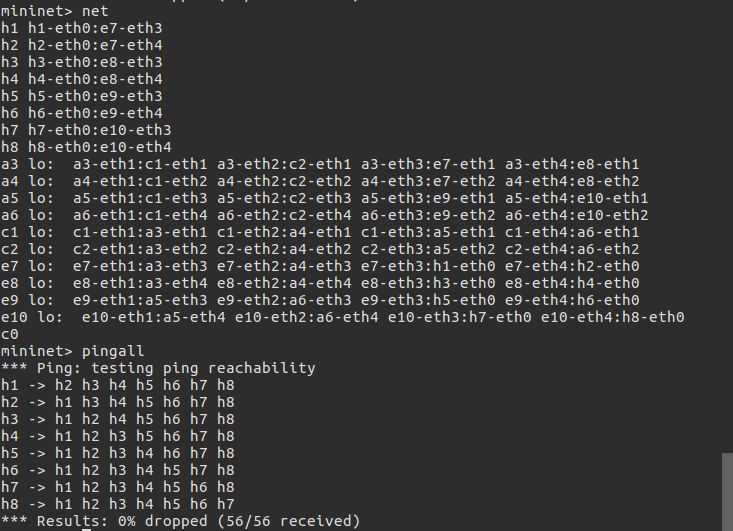
#!/usr/bin/python
#
"""Custom topology example
Adding the 'topos' dict with a key/value pair to generate our newly defined
topology enables one to pass in '--topo=mytopo' from the command line.
"""

from mininet.topo import Topo
from mininet.net import Mininet
from mininet.node import RemoteController,CPULimitedHost
from mininet.link import TCLink
from mininet.util import dumpNodeConnections

class MyTopo( Topo ):
    "Simple topology example."

    def __init__( self ):
        "Create custom topo."

        # Initialize topology
        Topo.__init__( self )
        L1 = 2
        L2 = L1 * 2
        L3 = L2
        c = []
        a = []
        e = []

        # add core ovs
        for i in range( L1 ):
                sw = self.addSwitch( 'c{}'.format( i + 1 ) )
                c.append( sw )

        # add aggregation ovs
        for i in range( L2 ):
                sw = self.addSwitch( 'a{}'.format( L1 + i + 1 ) )
                a.append( sw )

        # add edge ovs
        for i in range( L3 ):
                sw = self.addSwitch( 'e{}'.format( L1 + L2 + i + 1 ) )
                e.append( sw )

        # add links between core and aggregation ovs
        for i in range( L1 ):
                sw1 = c[i]
                for sw2 in a[i/2::L1/2]:
                # self.addLink(sw2, sw1, bw=10, delay='5ms', loss=10, max_queue_size=1000, use_htb=True)
                        self.addLink( sw2, sw1 )

        # add links between aggregation and edge ovs
        for i in range( 0, L2, 2 ):
                for sw1 in a[i:i+2]:
                    for sw2 in e[i:i+2]:
                        self.addLink( sw2, sw1 )

        #add hosts and its links with edge ovs
        count = 1
        for sw1 in e:
                for i in range(2):
                    host = self.addHost( 'h{}'.format( count ) )
                    self.addLink( sw1, host )
                    count += 1
topos = { 'mytopo': ( lambda: MyTopo() ) }