10分钟明白对偶建模法 / +Leampms的“主模型建模”和“对偶模型建模” 之 —— 三类最短路径问题
摘要
对偶模型建模是非常有独特的一种建模方式 —— 当问题本身要求指标极小的情况下,对偶模型表现为求极大。本文给出三种最短路径问题的线性规划/混合整数规划模型,其中的第三类最短路径问题采用对偶建模方法。一般情况下采用对偶模型建模并非为对偶而对偶,原因是有些问题采用对偶方式更容易表达。值得注意的是对偶模型的非最优可行解是被建模问题的非可行解,但对偶最优解既是被建模问题的可行解又是被建模问题的最优解。
本文及本博客中所有博文均为原创!
名词及知识点
对偶模型建模 —— 通过对偶方式把实际问题建模为原问题的对偶模型,对偶模型的特征之一是模型目标的极大极小方向与实际问题的极大极小方向正好相反 (不好懂?正常!看第三个模型你就秒懂)。
点对最短路径问题——在一个有向图(或无向图,本文都以有向图为例)上指定节点对 $start$和$end$, 求从$start$到$end$的最短路径。
单点最短路径问题——在一个有向图(或无向图)上指定单个节点start, 求从start到所有节点的最短路径。
全最短路径问题——对一个有向图 $G=(V,E)$, 求所有点对 $i \in V$, $j \in V$ 的最短路径。
边和节点的符号定义
对图$G=(V,E)$, 其中$V$是节点集合, $E$是边的集合,对边进行编号k=1,...,m, 对节点进行编号j=1,...,n。对边k, 其第一个顶点记为alpha[k],简记为a[k];第二个顶点记为beta[k],简记为b[k]。边k上的权(长度)记为c[k]。
问题1:点对最短路径
问题:求下图从节点1到节点11的最短路径。

建模:点对最短路径的模型常见于各大教科书中。
用0-1变量x[i][j] 表示边 (i,j) 是否被包含在从$start$到$end$的最短路径中,x[i][j]=1表示包含在内,x[i][j]=0表示不包含在内。使用边记号k进行累和,路径的长度为sum{k=1,...,m} c[k] x[a[k]][b[k]]。用主建模方法,目标为:
minimize sum{k=1,...,m} c[k] x[a[k]][b[k]] //(1)
对任意的节点i,如果i≠start并且i≠end, 则无论其在路径上与否,其入次sum{*}x[*][i]和出次sum{*}x[i][*]必须相等。于是有如下约束:
sum{k=1,...,m;b[k]==i}x[a[k]][i] = sum{k=1,...,m;a[k]==i}x[i][b[k]] | i=1,...,n; i<>start;i<>end //(2)
对于start节点来说,其出次等于1;对end节点来说,其入次等于1。即:
sum{k=1,...,m;a[k]==start}x[start][b[k]]=1 //(3)
sum{k=1,...,m;b[k]==end}x[a[k]][end]=1 //(4)
完整+Leapms模型:
min sum{k=1,...,m}x[a[k]][b[k]]c[k] //(1)
subject to
sum{k=1,...,m;b[k]==i}x[a[k]][i] = -->
sum{k=1,...,m;a[k]==i}x[i][b[k]]-->
|i=1,...,n; i<>start;i<>end //(2)
sum{k=1,...,m;a[k]==start}x[start][b[k]]=1 //(3)
sum{k=1,...,m;b[k]==end}x[a[k]][end]=1 //(4)
where
m,n,start,end are integers
e are sets
a[k],b[k],c[k] are numbers|k=1,...,m
x[i][j] is a variable of binary|i=1,...,n;j=1,...,n;i<>j
data_relation
m=_$(e)/3
a[k]=e[3k-2] | k=1,...,m
b[k]=e[3k-1] | k=1,...,m
c[k]=e[3k] | k=1,...,m
n=0
n=max(n,a[k])| k=1,...,m
n=max(n,b[k])| k=1,...,m
data
start=1
end=11
e={
1 2 12
1 3 16
1 4 7
1 5 21
2 6 5
3 6 6
3 7 3
4 7 5
5 9 15
5 13 11
6 8 4
7 8 9
7 9 27
8 10 24
8 12 9
9 11 23
9 14 5
10 11 8
11 14 16
12 9 10
12 10 14
13 9 6
13 14 12
}
在+Leapms环境中使用load, mip命令求解过程如下(请展开查看):
+Leapms>load
Current directory is "ROOT".
.........
ShortestPath1.leap
ShortestPath2.leap
ShortestPath3.leap
ShortestPath4.leap
.........
please input the filename:ShortestPath1
================================================================
1: min sum{k=1,...,m}x[a[k]][b[k]]c[k] //(1)
2: subject to
3: sum{k=1,...,m;b[k]==i}x[a[k]][i] = -->
4: sum{k=1,...,m;a[k]==i}x[i][b[k]]-->
5: |i=1,...,n; i<>start;i<>end //(2)
6:
7: sum{k=1,...,m;a[k]==start}x[start][b[k]]=1 //(3)
8: sum{k=1,...,m;b[k]==end}x[a[k]][end]=1 //(4)
9:
10: where
11: m,n,start,end are integers
12: e are sets
13: a[k],b[k],c[k] are numbers|k=1,...,m
14: x[i][j] is a variable of binary|i=1,...,n;j=1,...,n;i<>j
15:
16: data_relation
17: m=_$(e)/3
18: a[k]=e[3k-2] | k=1,...,m
19: b[k]=e[3k-1] | k=1,...,m
20: c[k]=e[3k] | k=1,...,m
21: n=0
22: n=max(n,a[k])| k=1,...,m
23: n=max(n,b[k])| k=1,...,m
24: data
25: start=1
26: end=11
27: e={
28: 1 2 12
29: 1 3 16
30: 1 4 7
31: 1 5 21
32: 2 6 5
33: 3 6 6
34: 3 7 3
35: 4 7 5
36: 5 9 15
37: 5 13 11
38: 6 8 4
39: 7 8 9
40: 7 9 27
41: 8 10 24
42: 8 12 9
43: 9 11 23
44: 9 14 5
45: 10 11 8
46: 11 14 16
47: 12 9 10
48: 12 10 14
49: 13 9 6
50: 13 14 12
51: }
52:
53:
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=182
number of constraints=14
..................................
+Leapms>mip
relexed_solution=52; number_of_nodes_branched=0; memindex=(2,2)
The Problem is solved to optimal as an MIP.
找到整数规划的最优解.非零变量值和最优目标值如下:
.........
x1_4* =1
x4_7* =1
x7_8* =1
x8_12* =1
x10_11* =1
x12_10* =1
.........
Objective*=52
.........
+Leapms>
求解过程
求解结果,路径长52,路径如图。

问题2:单点最短路径
问题:求问题1图从节点start=1到其余所有节点的最短路径。
建模:单点最短路径模型在教科书中不常见,但求此问题的Dijkstra算法很普及。
以下建模方法为本文未参考任何其他书籍和文章情况下的原创,但不能保证类似模型未曾出现在其他书或文中:
设从start到节点i的最短路径长度为d[i]。
采用主模型建模,目标显然可以是:
minimize sum{i=1,...,n}d[i] //(5)
从节点start到自身的最短路径长度为0:
d[start]=0 //(6)
用0-1变量x[i][j] 表示边 (i,j) 是否被包含在从$start$到其余节点的最短路径上,于是对任意定点i≠start, 其入次和sum{*}x[*][i] 等于1。即:
sum{k=1,...,m;b[k]==i}x[a[k]][i]=1|i=1,...,n; i<>start //(7)
如果边k在任意最短路径上,那么到b[k]节点的最短路径长度d[b[k]]将不小于到b[k]的紧前节点a[k]的最短路径长度d[a[k]]加边k的长度c[k],即:
d[b[k]]> = d[a[k]] + c[k] - (1-x[a[k]][b[k]])bigM | k=1,...,m //(8)
约束(8)中的bigM是足够大的数。例如取为所有变长的和即可。
完整+Leapms模型:
minimize sum{i=1,...,n}d[i] //(5)
subject to
d[start]=0 //(6)
sum{k=1,...,m;b[k]==i}x[a[k]][i]=1|i=1,...,n; i<>start //(7)
d[b[k]]>= d[a[k]]+c[k]-(1-x[a[k]][b[k]])bigM | k=1,...,m //(8)
where
m,n,start are integers
e are sets
bigM is a number
a[k],b[k],c[k] are numbers|k=1,...,m
d[i] is a variable of nonnegative number|i=1,...,n
x[i][j] is a variable of binary|i=1,...,n;j=1,...,n;i<>j
data_relation
m=_$(e)/3
a[k]=e[3k-2] | k=1,...,m
b[k]=e[3k-1] | k=1,...,m
c[k]=e[3k] | k=1,...,m
n=0
n=max(n,a[k])| k=1,...,m
n=max(n,b[k])| k=1,...,m
bigM=sum{k=1,...,n}c[k]
data
start=1
e={
1 2 12
1 3 16
1 4 7
1 5 21
2 6 5
3 6 6
3 7 3
4 7 5
5 9 15
5 13 11
6 8 4
7 8 9
7 9 27
8 10 24
8 12 9
9 11 23
9 14 5
10 11 8
11 14 16
12 9 10
12 10 14
13 9 6
13 14 12
}
在+Leapms环境中使用load, mip命令求解过程如下(请展开查看):
+Leapms>load
Current directory is "ROOT".
.........
ShortestPath1.leap
ShortestPath2.leap
ShortestPath3.leap
ShortestPath4.leap
.........
please input the filename:shortestPath3
================================================================
1: minimize sum{i=1,...,n}d[i] //(5)
2: subject to
3: d[start]=0 //(6)
4: sum{k=1,...,m;b[k]==i}x[a[k]][i]=1|i=1,...,n; i<>start //(7)
5: d[b[k]]>= d[a[k]]+c[k]-(1-x[a[k]][b[k]])bigM | k=1,...,m //(8)
6: where
7: m,n,start are integers
8: e are sets
9: bigM is a number
10: a[k],b[k],c[k] are numbers|k=1,...,m
11: d[i] is a variable of nonnegative number|i=1,...,n
12: x[i][j] is a variable of binary|i=1,...,n;j=1,...,n;i<>j
13:
14: data_relation
15: m=_$(e)/3
16: a[k]=e[3k-2] | k=1,...,m
17: b[k]=e[3k-1] | k=1,...,m
18: c[k]=e[3k] | k=1,...,m
19: n=0
20: n=max(n,a[k])| k=1,...,m
21: n=max(n,b[k])| k=1,...,m
22: bigM=sum{k=1,...,n}c[k]
23: data
24: start=1
25: e={
26: 1 2 12
27: 1 3 16
28: 1 4 7
29: 1 5 21
30: 2 6 5
31: 3 6 6
32: 3 7 3
33: 4 7 5
34: 5 9 15
35: 5 13 11
36: 6 8 4
37: 7 8 9
38: 7 9 27
39: 8 10 24
40: 8 12 9
41: 9 11 23
42: 9 14 5
43: 10 11 8
44: 11 14 16
45: 12 9 10
46: 12 10 14
47: 13 9 6
48: 13 14 12
49: }
50:
51:
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=196
number of constraints=37
..................................
+Leapms>mip
relexed_solution=97; number_of_nodes_branched=0; memindex=(2,2)
The Problem is solved to optimal as an MIP.
找到整数规划的最优解.非零变量值和最优目标值如下:
.........
d2* =12
d3* =16
d4* =7
d5* =21
d6* =17
d7* =12
d8* =21
d9* =36
d10* =44
d11* =52
d12* =30
d13* =32
d14* =41
x1_2* =1
x1_3* =1
x1_4* =1
x1_5* =1
x2_6* =1
x4_7* =1
x5_9* =1
x5_13* =1
x6_8* =1
x8_12* =1
x9_14* =1
x10_11* =1
x12_10* =1
.........
Objective*=341
.........
+Leapms>
求解过程
根据求解结果,路径表现为根为start=1的树:
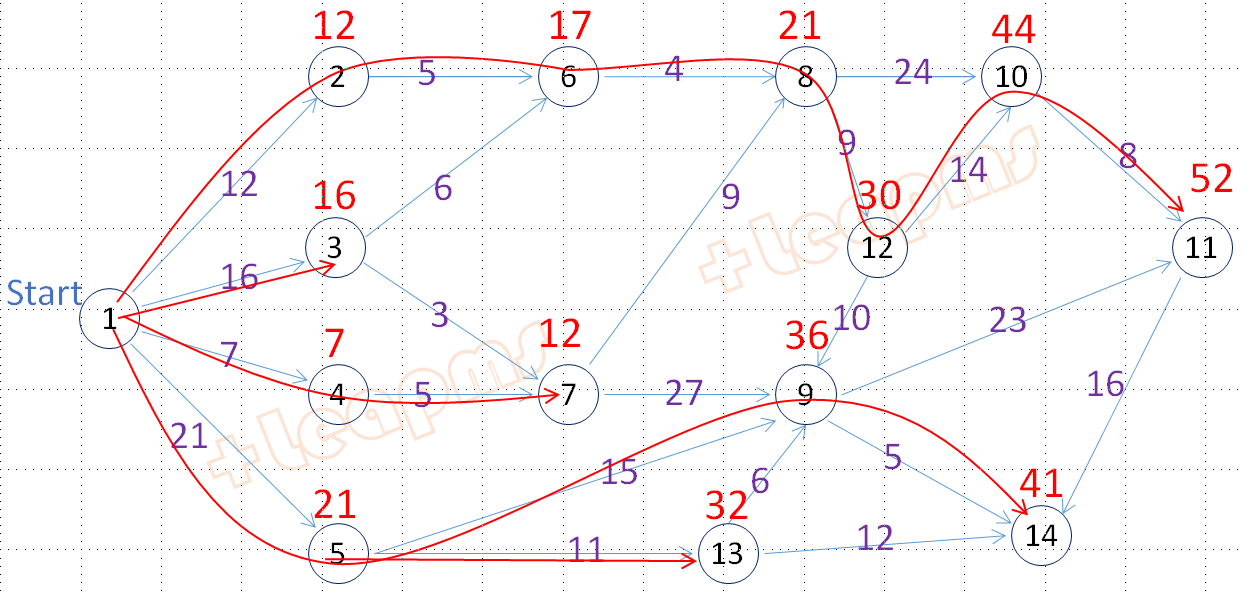
全最短路径问题对偶建模方法
问题:求问题1图任意两节点i,j之间的最短路径。
建模:全最短路径模型在教科书中及其少见,但教科书中普遍介绍求解此问题的floyd算法。
以下建模方法为本文未参考任何其他书籍和文章情况下的原创,但不能保证类似模型未曾出现在其他书或文中:
设节点i,j之间的最短路径的长度为d[i][j], 采用对偶模型建模方法 —— 极大化所有d[i][j]之和!
maximize sum{i=1,...,n;j=1,...,n}d[i][j] //(9)
约束一、d[i][j] 不大于 i,j之间的边长
d[i][j]<=D[i][j] | i=1,...,n;j=1,...,n //(10)
约束二、d[i][j] 不大于绕行第三点k的距离和,即d[i][j] <= d[i][k] + d[j][j] :
d[i][j]<=d[i][k]+d[k][j] -->
| i=1,...,n;j=1,...,n;k=1,...,n;i<>j;i<>k;j<>k //(11)
完整+Leapms模型:
maximize sum{i=1,...,n;j=1,...,n}d[i][j] //(9)
subject to
d[i][j]<=D[i][j] | i=1,...,n;j=1,...,n //(10)
d[i][j]<=d[i][k]+d[k][j] -->
| i=1,...,n;j=1,...,n;k=1,...,n;i<>j;i<>k;j<>k //(11)
where
m,n are integers
e are sets
bigM is a number
D[i][j] is a number | i=1,...,n;j=1,...,n;i<>j
d[i][j] is a variable of nonnegative number | i=1,...,n;j=1,...,n
data_relation
m=_$(e)/3
n=0
n=max(n,e[3k-2]) | k=1,...,m
n=max(n,e[3k-1]) | k=1,...,m
bigM=10000
D[i][i]=0 | i=1,...,n
D[i][j]=bigM | i=1,...,n;j=1,...,n;i<>j
D[e[3k-2]][e[3k-1]]=e[3k] | k=1,...,m
data
e={
1 2 12
1 3 16
1 4 7
1 5 21
2 6 5
3 6 6
3 7 3
4 7 5
5 9 15
5 13 11
6 8 4
7 8 9
7 9 27
8 10 24
8 12 9
9 11 23
9 14 5
10 11 8
11 14 16
12 9 10
12 10 14
13 9 6
13 14 12
}
在+Leapms环境中使用load, cplex命令(调用cplex求解器求解)求解过程如下(请展开查看):
+Leapms>load
Current directory is "ROOT".
.........
ShortestPath1.leap
ShortestPath2.leap
ShortestPath3.leap
ShortestPath4.leap
.........
please input the filename:ShortestPath4
================================================================
1: maximize sum{i=1,...,n;j=1,...,n}d[i][j] //(9)
2: subject to
3: d[i][j]<=D[i][j] | i=1,...,n;j=1,...,n //(10)
4: d[i][j]<=d[i][k]+d[k][j] -->
5: | i=1,...,n;j=1,...,n;k=1,...,n;i<>j;i<>k;j<>k //(11)
6: where
7: m,n are integers
8: e are sets
9: bigM is a number
10: D[i][j] is a number | i=1,...,n;j=1,...,n;i<>j
11: d[i][j] is a variable of nonnegative number | i=1,...,n;j=1,...,n
12:
13: data_relation
14: m=_$(e)/3
15: n=0
16: n=max(n,e[3k-2]) | k=1,...,m
17: n=max(n,e[3k-1]) | k=1,...,m
18: bigM=10000
19: D[i][i]=0 | i=1,...,n
20: D[i][j]=bigM | i=1,...,n;j=1,...,n;i<>j
21: D[e[3k-2]][e[3k-1]]=e[3k] | k=1,...,m
22: data
23: e={
24: 1 2 12
25: 1 3 16
26: 1 4 7
27: 1 5 21
28: 2 6 5
29: 3 6 6
30: 3 7 3
31: 4 7 5
32: 5 9 15
33: 5 13 11
34: 6 8 4
35: 7 8 9
36: 7 9 27
37: 8 10 24
38: 8 12 9
39: 9 11 23
40: 9 14 5
41: 10 11 8
42: 11 14 16
43: 12 9 10
44: 12 10 14
45: 13 9 6
46: 13 14 12
47: }
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=196
number of constraints=2380
..................................
+Leapms>cplex
You must have licience for Ilo Cplex, otherwise you will violate
corresponding copyrights, continue(Y/N)?
你必须有Ilo Cplex软件的授权才能使用此功能,否则会侵犯相应版权,
是否继续(Y/N)?y
+Leapms> Tried aggregator 1 time.
LP Presolve eliminated 196 rows and 14 columns.
Reduced LP has 2184 rows, 182 columns, and 6552 nonzeros.
Presolve time = 0.02 sec. (1.03 ticks) Iteration log . . .
Iteration: 1 Dual objective = 1580277.000000
Solution status = Optimal
Solution value = 1.14154e+006
d1_2=12
d1_3=16
d1_4=7
d1_5=21
d1_6=17
d1_7=12
d1_8=21
d1_9=36
d1_10=44
d1_11=52
d1_12=30
d1_13=32
d1_14=41
d2_1=10000
d2_3=10000
d2_4=10000
d2_5=10000
d2_6=5
d2_7=10000
d2_8=9
d2_9=28
d2_10=32
d2_11=40
d2_12=18
d2_13=10000
d2_14=33
d3_1=10000
d3_2=10000
d3_4=10000
d3_5=10000
d3_6=6
d3_7=3
d3_8=10
d3_9=29
d3_10=33
d3_11=41
d3_12=19
d3_13=10000
d3_14=34
d4_1=10000
d4_2=10000
d4_3=10000
d4_5=10000
d4_6=10000
d4_7=5
d4_8=14
d4_9=32
d4_10=37
d4_11=45
d4_12=23
d4_13=10000
d4_14=37
d5_1=10000
d5_2=10000
d5_3=10000
d5_4=10000
d5_6=10000
d5_7=10000
d5_8=10000
d5_9=15
d5_10=10000
d5_11=38
d5_12=10000
d5_13=11
d5_14=20
d6_1=10000
d6_2=10000
d6_3=10000
d6_4=10000
d6_5=10000
d6_7=10000
d6_8=4
d6_9=23
d6_10=27
d6_11=35
d6_12=13
d6_13=10000
d6_14=28
d7_1=10000
d7_2=10000
d7_3=10000
d7_4=10000
d7_5=10000
d7_6=10000
d7_8=9
d7_9=27
d7_10=32
d7_11=40
d7_12=18
d7_13=10000
d7_14=32
d8_1=10000
d8_2=10000
d8_3=10000
d8_4=10000
d8_5=10000
d8_6=10000
d8_7=10000
d8_9=19
d8_10=23
d8_11=31
d8_12=9
d8_13=10000
d8_14=24
d9_1=10000
d9_2=10000
d9_3=10000
d9_4=10000
d9_5=10000
d9_6=10000
d9_7=10000
d9_8=10000
d9_10=10000
d9_11=23
d9_12=10000
d9_13=10000
d9_14=5
d10_1=10000
d10_2=10000
d10_3=10000
d10_4=10000
d10_5=10000
d10_6=10000
d10_7=10000
d10_8=10000
d10_9=10000
d10_11=8
d10_12=10000
d10_13=10000
d10_14=24
d11_1=10000
d11_2=10000
d11_3=10000
d11_4=10000
d11_5=10000
d11_6=10000
d11_7=10000
d11_8=10000
d11_9=10000
d11_10=10000
d11_12=10000
d11_13=10000
d11_14=16
d12_1=10000
d12_2=10000
d12_3=10000
d12_4=10000
d12_5=10000
d12_6=10000
d12_7=10000
d12_8=10000
d12_9=10
d12_10=14
d12_11=22
d12_13=10000
d12_14=15
d13_1=10000
d13_2=10000
d13_3=10000
d13_4=10000
d13_5=10000
d13_6=10000
d13_7=10000
d13_8=10000
d13_9=6
d13_10=10000
d13_11=29
d13_12=10000
d13_14=11
d14_1=10000
d14_2=10000
d14_3=10000
d14_4=10000
d14_5=10000
d14_6=10000
d14_7=10000
d14_8=10000
d14_9=10000
d14_10=10000
d14_11=10000
d14_12=10000
d14_13=10000
运行过程
模型中的bigM取为10000,结果中的d[*][*]=10000表示对应两节点之间不存在路径。
具体路径通过d[*][*]数值反向推知。下图是节点4到其他节点的最短路径树,通过d[4][*]反向推知。
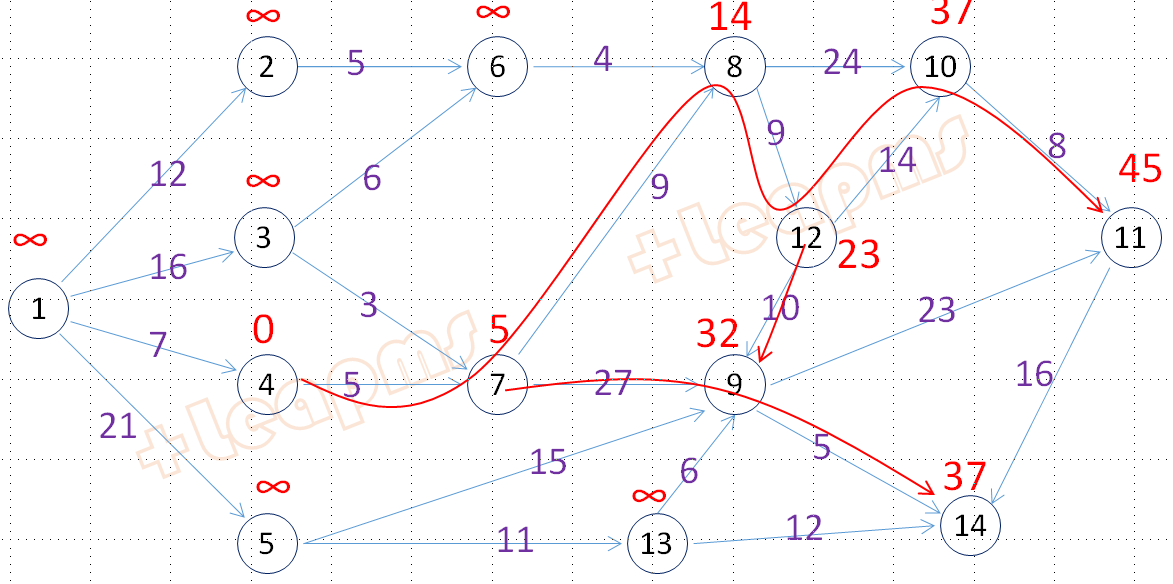
10分钟明白对偶建模法 / +Leampms的“主模型建模”和“对偶模型建模” 之 —— 三类最短路径问题的更多相关文章
- 如何从40亿整数中找到不存在的一个 webservice Asp.Net Core 轻松学-10分钟使用EFCore连接MSSQL数据库 WPF实战案例-打印 RabbitMQ与.net core(五) topic类型 与 headers类型 的Exchange
如何从40亿整数中找到不存在的一个 前言 给定一个最多包含40亿个随机排列的32位的顺序整数的顺序文件,找出一个不在文件中的32位整数.(在文件中至少确实一个这样的数-为什么?).在具有足够内存的情况 ...
- JavaScript 10分钟入门
JavaScript 10分钟入门 随着公司内部技术分享(JS进阶)投票的失利,先译一篇不错的JS入门博文,方便不太了解JS的童鞋快速学习和掌握这门神奇的语言. 以下为译文,原文地址:http://w ...
- emacs最简单入门,只要10分钟
macs最简单入门,只要10分钟 windwiny @2013 无聊的时候又看到鼓吹emacs的文章,以前也有几次想尝试,结果都是玩不到10分钟就退出删除了. 这次硬着头皮,打开几篇文章都看完 ...
- 不用搭环境的10分钟AngularJS指令简易入门01(含例子)
不用搭环境的10分钟AngularJS指令简易入门01(含例子) `#不用搭环境系列AngularJS教程01,前端新手也可以轻松入坑~阅读本文大概需要10分钟~` AngularJS的指令是一大特色 ...
- 中国移动能力开放商店OneNET View数据可视化公测 10分钟轻便生成行业可视化界面
随着云计算,5G技术,人工智能等底层技术的发展,万物互联时代已经到来,同时带来了海量数据,如何效果好.低成本.短时间的表现据,成为物联网行业从业者和公司的当务之急. OneNET View传统的数据展 ...
- Python数据分析Pandas库之熊猫(10分钟二)
pandas 10分钟教程(二) 重点发法 分组 groupby('列名') groupby(['列名1','列名2',.........]) 分组的步骤 (Splitting) 按照一些规则将数据分 ...
- 10分钟轻松设置出 A+ 评分的 HTTP/2 网站
前言 其实 HTTP/2 应该是 2015 年的老话题了(2015 年 5 月 14 日 HTTP/2 协议正式版的发布),但是 2018 年都到了很多网站依旧没有使用,作为新一代互联网协议,HTTP ...
- 10分钟,利用canvas画一个小的loading界面
首先利用定义下canvas得样式 <canvas width="1024" height="720" id="canvas" styl ...
- 10分钟学会Less开发环境搭建与初体验
Less 是一门 CSS 预处理语言,它扩充了 CSS 语言,增加了诸如变量.混合(mixin).函数等功能,让 CSS 更易维护.方便制作主题.扩充. 今天看一下,10分钟能不能手把手快速教会你Le ...
随机推荐
- Goroutine陷阱
Go在语言层面通过Goroutine与channel来支持并发编程,使并发编程看似变得异常简单,但通过最近一段时间的编码,越来越觉得简单的东西,很容易会被滥用.Java的标准库也让多线程编程变得简单, ...
- Spring Boot自动配置源码解析(基于Spring Boot 2.0.2.RELEASE)
在Spring Boot官方介绍中,首一段话是这样的(如下图).我们可以大概了解到其所表达的含义:我们可以利用Spring Boot写很少的配置来创建一个非常方便的基于Spring整合第三方类库的单体 ...
- 【最小生成树】UVA1494Qin Shi Huang's National Road System秦始皇修路
Description During the Warring States Period of ancient China(476 BC to 221 BC), there were seven ki ...
- 从字节码和JVM的角度解析Java核心类String的不可变特性
1. 前言 最近看到几个有趣的关于Java核心类String的问题. String类是如何实现其不可变的特性的,设计成不可变的好处在哪里. 为什么不推荐使用+号的方式去形成新的字符串,推荐使用Stri ...
- Ubuntu18.04美化主题(mac主题)
前端时间Ubuntu18.04LTS发布,碰巧之前用的Ubuntu16.04出了一点问题,懒得解决,索性就换了Ubuntu18.04. 成果: 参考博客:https://www.cnblogs.com ...
- selenium IDE工具页面介绍!
selenium IDE工具页面,常用功能点介绍
- css中固定宽高div与不固定宽高div垂直居中的处理办法
固定高宽div垂直居中 如上图,固定高宽的很简单,写法如下: position: absolute; left: 50%; top: 50%; width:200px; height:100px; m ...
- 8天入门docker系列 —— 第四天 使用aspnetcore小案例熟悉端口映射和挂载目录
到目前为止大家应该对镜像和容器有了一个大概认知,而且也用了docker进行了一个简单化的部署,但仔细一看问题还有很多,所以这篇我们继续完善. 一:如何让外网访问到容器内应用 我们知道容器内拥有自己的子 ...
- Gradle入门到实战(一) — 全面了解Gradle
声明:本文来自汪磊的博客,转载请注明出处 可关注个人公众号,那里更新更及时,阅读体验更好: 友情提示由于文章是从个人公众号拷贝过来整理的,发现图片没有正常显示,没关注公众号的同学可通过如下链接查看: ...
- 原生js实现 五子棋
先初始化棋盘 HTML: <!--棋盘--> <div class="grid"></div> CSS: /*棋盘*/ .grid{ posit ...
