[题解]ybt1365：FBI树(fbi)

ybt1365：FBI树(fbi)

[题目描述]

我们可以把由“0”和“1”组成的字符串分为三类：全“0”串称为B串，全“1”串称为I串，既含“0”又含“1”的串则称为F串。

FBI树是一种二叉树，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为2N的“01”串S可以构造出一棵FBI树T，递归的构造方法如下：

T的根结点为R，其类型与串S的类型相同；

若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2；由左子串S1构造R的左子树T1，由右子串S2构造R的右子树T2。

现在给定一个长度为2N的“01”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历序列。

[输入格式]

第一行是一个整数N（0 ≤ N ≤ 10），第二行是一个长度为2N的“01”串。

[输出格式]

一行，这一行只包含一个字符串，即FBI树的后序遍历序列。

[输入样例]

3

10001011

[输出样例]

IBFBBBFIBFIIIFF

[解法1（常规建树）]

请看任天祥大佬代码：

 #include<cstdio>

 #include<iostream>

 #include<cstring>

 #include<cstdlib>

 using namespace std;

 int N;

 struct FBI

 {

     FBI *l,*r;

     char R;

 }*root;

 void build(string c,FBI **pr)      //新建节点的串与该节点位置

 {

       FBI *d;

     d=(FBI *)malloc(sizeof(FBI));              //位置申请空间

     if(c.length()==)                   //边界

     {

         switch (c[])          

         {

             case '': d->R='B';//识别

             break;

             case '': d->R='I';

             break;

         }

         *pr=d;

         d->l=NULL;         //这两句贼重要，要不然输出无边界。

         d->r=NULL;

         return;

     }

       int mid=c.length()/;       //串分两半

     string s1,s2;                       //串分两半

     s1=c.substr(,mid);

     s2=c.substr(mid,mid);              //指针指空

     FBI *dl,*dr;

     build(s1,&(d->l));                    //递归建树

     build(s2,&(d->r));  

       dl=d->l;

     dr=d->r;                 

     if((dl)->R=='B'&&(dr)->R=='B')

     {

         d->R='B';

         *pr=d;

         return;

     }

     if((dl)->R=='I'&&(dr)->R=='I')

     {

         d->R='I';

         *pr=d;

         return;

     }

     else d->R='F';

     *pr=d;

     return;

 }

 void backprin(FBI *a)

 {

     if(a)

     {

        backprin(a->l);

        backprin(a->r);

        printf("%c",a->R);

        return;

       }

 }

 int main ()

 {

       freopen("in.in","r",stdin);

       freopen("std.out","w",stdout);

     scanf("%d",&N);

     string x;

     cin>>x;

     build(x,&root);

     backprin(root);

     return ;

 }

[解法2（递归骚代码）]

仔细观察我们就会发现对于一部分01串[l,r]对应节点i的fbi只与它左右两个子节点的fbi决定，而左右两个子节点对应的01串分别就是[l,(r+l)/2]和[(r+l)/2+1,r]由此我们可以得到递归式：

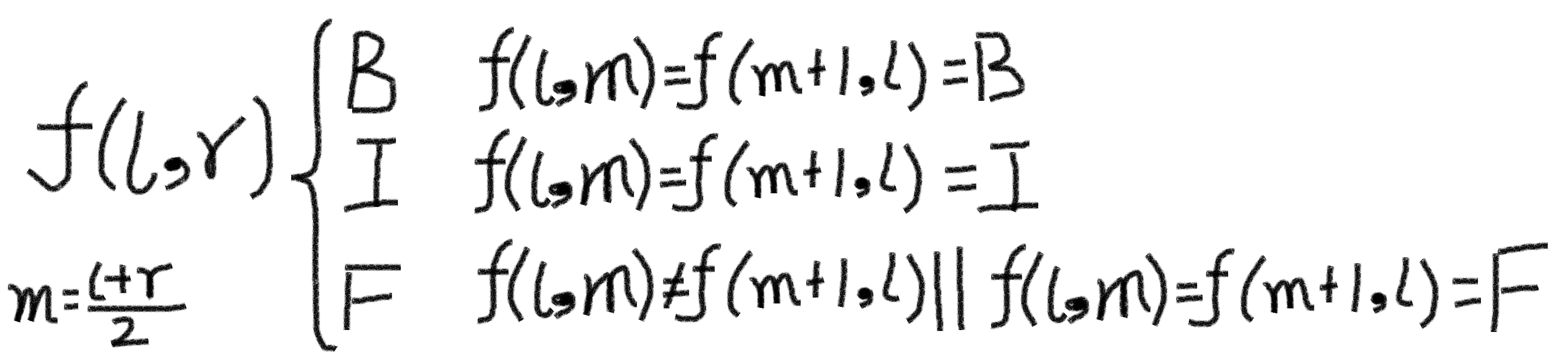
递归终点就是l=r直接返回这个01串对应值就好。如此我们得到了一下代码：

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<string>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 bool fbi[];
 char dfs(int left,int right){
     if(left==right){
         if(fbi[left]){
             printf("I");
             return 'I';
         }
         else{
             printf("B");
             return 'B';
         }
     }
     char l=dfs(left,left+(right-left)/);
     char r=dfs(left+(right-left)/+,right);
     if(l=='F'||r=='F'){
         printf("F");
         return 'F';
     }
     if(l==r){
         printf("%c",l);
         return l;
     }
     else {
         printf("F");
         return 'F';
     }
 }
 int main(){
     int n;
     scanf("%d",&n);
     n=pow(,n);
     char temp;
     for(int i=;i<=n;++i){
         scanf("\n%c",&temp);
         fbi[i]=temp-'';
     }
     dfs(,n);
     return ;
 }

2019-01-06 22:57:10