关联分析中寻找频繁项集的FP-growth方法

关联分析是数据挖掘中常用的分析方法。一个常见的需求比如说寻找出经常一起出现的项目集合。

引入一个定义，项集的支持度（support），是指所有包含这个项集的集合在所有数据集中出现的比例。

规定一个最小支持度，那么不小于这个最小支持度的项集称为频繁项集（frequent item set）。

如何找到数据集中所有的频繁项集呢？

最简单的方法是对所有项集进行统计，可以通过逐渐增大项集大小的方式来遍历所有项集。比如说下面的数据集，先统计所有单个元素集合的支持度，{z} 的支持度为5 （这里把项目出现次数作为支持度，方便描述），然后逐渐增大项集大小，比如{z,r} 的支持度为1

数据集ID	数据
001	r, z, h, j, p
002	z, y, x, w, v, u, t, s
003	z
004	r, x, n, o, s
005	y, r, x, z, q, t, p
006	y, z, x, e, q, s, t, m

显然这样的方式，计算量很大，当项目增多，项集的数目是指数增长的。当然我们也可以应用一些规律

1）如果一个项集是频繁项集，那么它的子集都是频繁项集

2）如果一个项集不是频繁项集，那么它的超集也不是频繁项集

Apriori算法就是应用了这些方法可以减少寻找频繁项集的计算。而FP-Growth算法则另辟蹊径，它在遍历数据的时候构造一个树结构，当树构造完成，每个节点记录的值就是这个节点到根节点路径上的项集的支持度。

首先对数据集中的数据按单个元素的支持度进行重排

数据集ID	数据	按单元数支持度重排后的数据
001	r, z, h, j, p	z, r
002	z, y, x, w, v, u, t, s	z, x, y, s, t
003	z	z
004	r, x, n, o, s	x, s, r
005	y, r, x, z, q, t, p	z, x, y, r, t
006	y, z, x, e, q, s, t, m	z, x, y, s, t

然后把每一行数依次拿来构建FP树。把重排后每一行数据从左到右入树。从空集开始，如果树中已存在现有元素，则增加现有元素的值；如果现有元素不存在，则向树添加一个分支。

树构造完成后，以{x:3}这个节点为例，它表示了从这个节点到根节点路径上集合{x,z}的支持度为3。

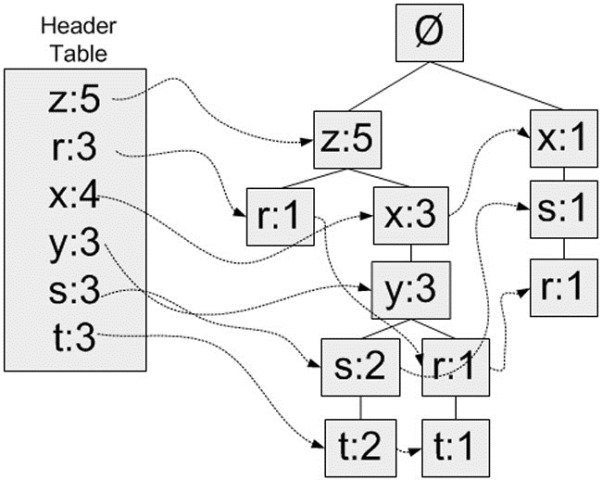
那么问题来了，我们如何保证我们能获得所有的频繁项集，即支持度大于最小支持度的项集。是找出节点值大于最小支持度就够了吗？比如设最小支持度为3，从树上可以看出{z,x,y}的支持度为3，但是仔细观察{z,x,y,t}这个项集的支持度也是为3，如何做呢？

首先为每个元素的找到所有前缀路径，一条前缀路径，是指元素父节点到根节点的路径

单元素	前缀路径
z	{}: 5
r	{x, s}: 1, {z, x, y}: 1, {z}: 1
x	{z}: 3, {}: 1
y	{z, x}: 3
s	{z, x, y}: 2, {x}: 1
t	{z, x, y, s}: 2, {z, x, y, r}: 1

然后对每个元素的所有前缀路径再执行一次FP树的构造过程，这样看到去除这个元素后能得到什么样的频繁项集。如下可以顺利得出{z,x,y} + {t}是一个支持度为3的频繁项集。

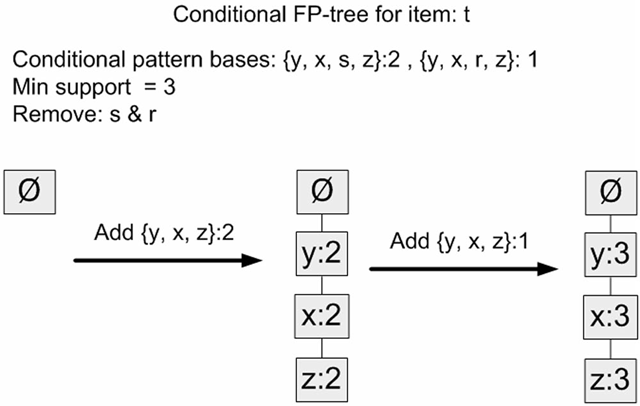
据此，FP-Growth方法就可以算出数据集中最小支持度为3的频繁项集：{z},{z,x},{z,x,y},{z,x,y,t}

参考：

1. https://www.cnblogs.com/qwertWZ/p/4510857.html