Borůvka algorithm

我好无聊啊，直接把wiki的算法介绍翻译一下把。

wiki关于Borůvka algorithm的链接：链接

Borůvka algorithm是一个在所有边权都是不同的图中找到最小生成树的贪心算法。（其实边权相同也可以做，具体见后文），或者在一个不联通的图找到最小生成树。

它由 Otakar Borůvka （人名）第一次发表在1926年，被作为给Moravia（一个地区）一种有效的电网建设方法。这个算法被Choquet在1938年重新发现，在1951年，它又被 Florek, Łukasiewicz, Perkal, Steinhaus, and Zubrzyck重新发现。又在1965年被Georges Sollin发现。这个算法经常被叫做Sollin's algorithm.特别在 parallel computing的文献中。

算法过程：

一开始每个点自成一个联通块。

每次所有联通块都找一条边权最小的边，其中一端在该联通块内而另一端不在，接下来加入这些边并合并联通块。

重复上述操作直到没有联通块可以合并。

一个细节：由于我们的写法问题，在边权相同的特殊情况下，我们会连接形成环，所以我们增加一个维度来排序。

看一下这东西流程：

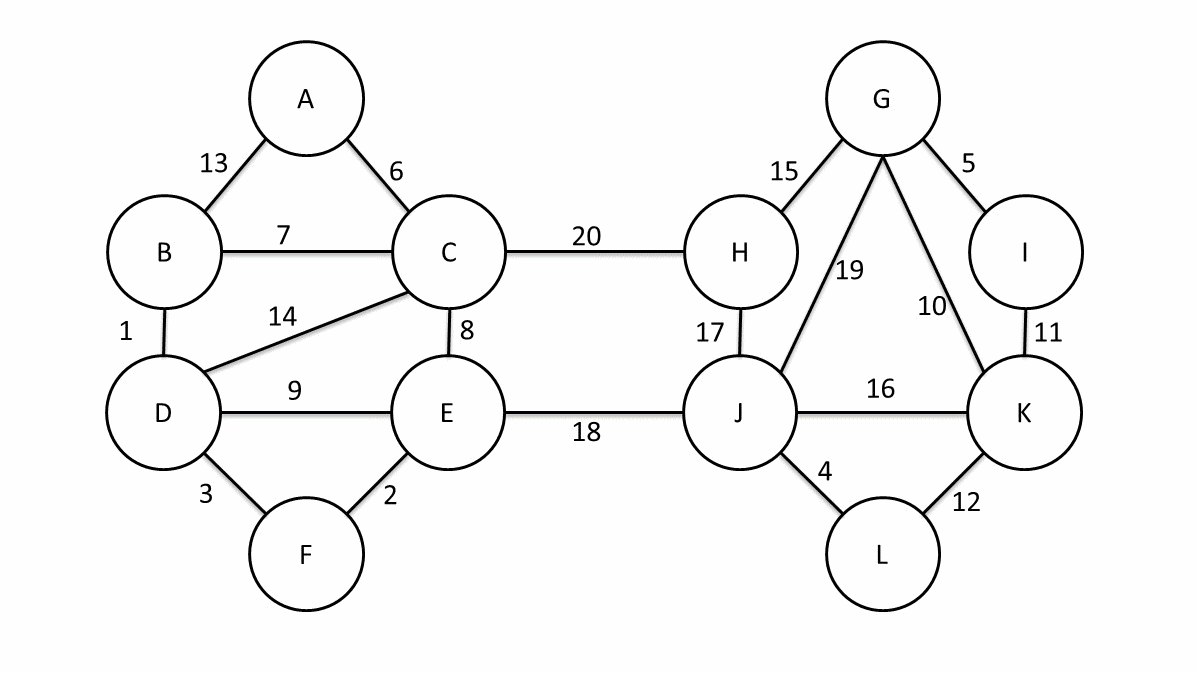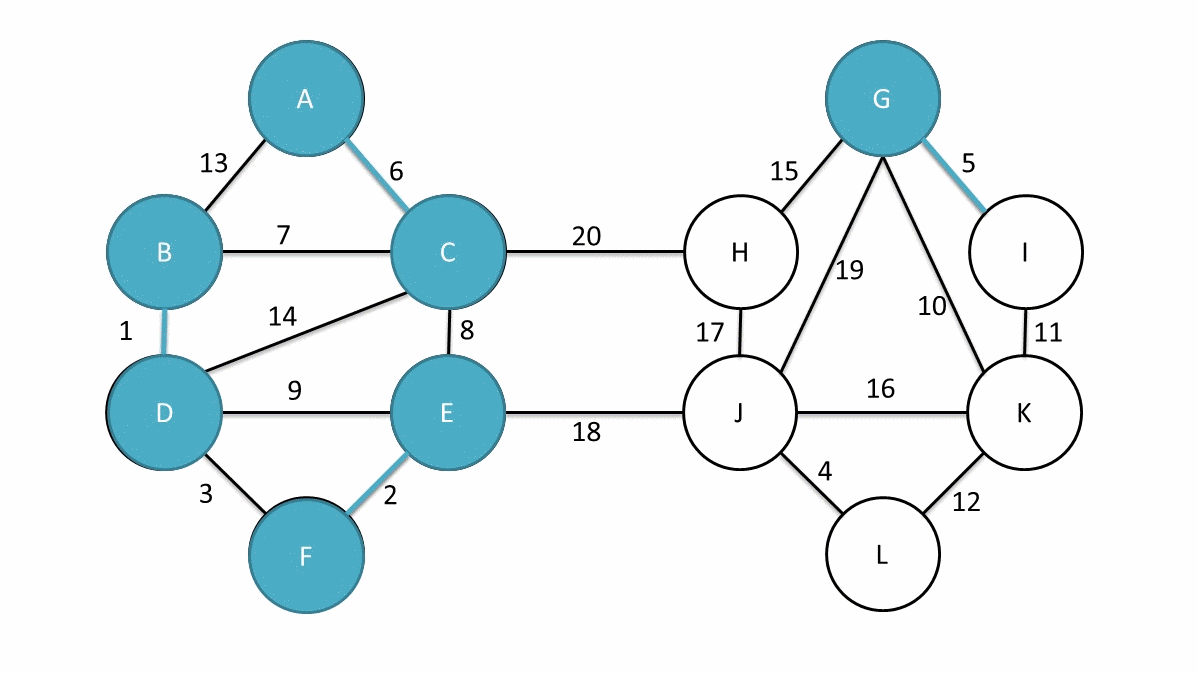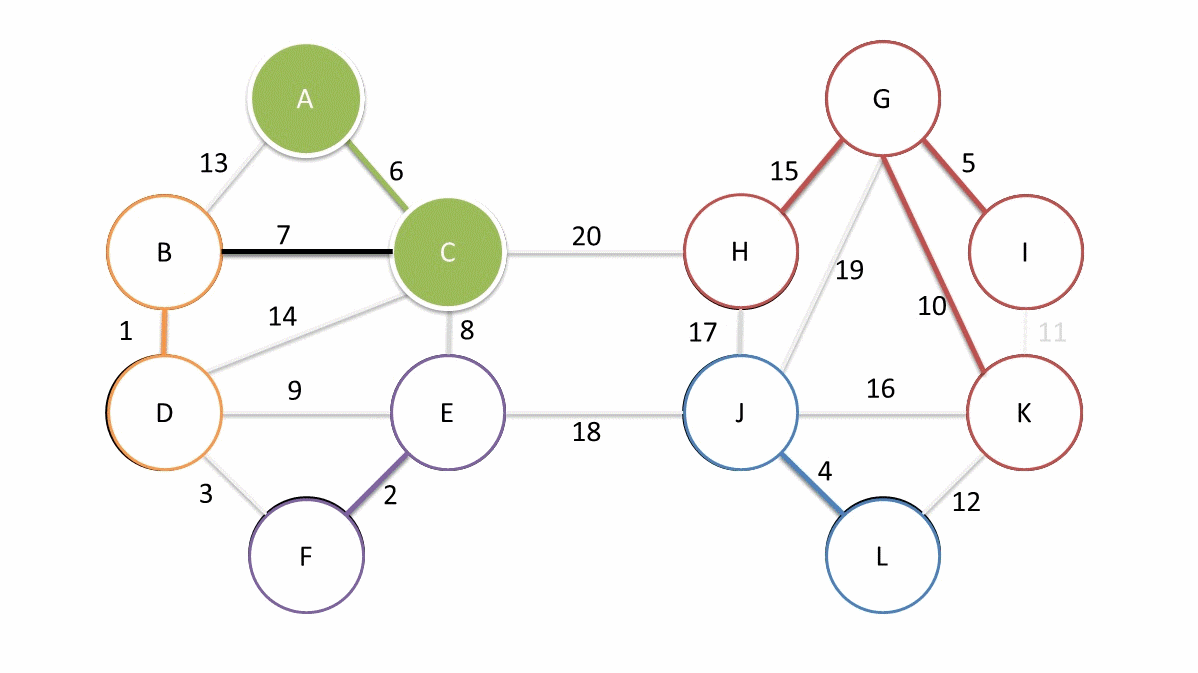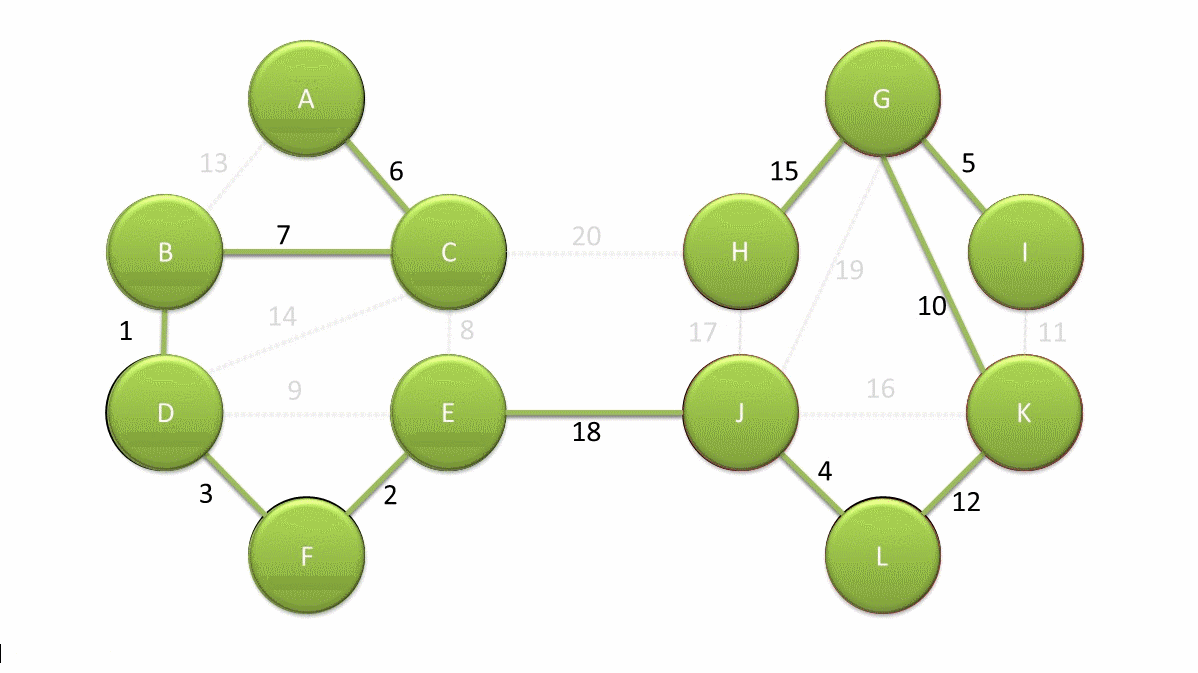
可以用切割性质证明算法的正确性。

切割性质：

将点集V分成S和V-S，一端在S内另一端在V-S内边权最小的边，一定出现在最小生成树中。

复杂度分析：

显然，联通块们，每次最小减少至原来的一般，每一次都要遍历每一条边，所以复杂度:$O(Elog_V)$

$$\color{white}{\text{完美结束，顺带试验一下透明字体}}$$

参考资料：

脑子

wiki

Tweetuzki

题目们

P3366 【模板】最小生成树

 CF888G

UOJ 240

模板题的代码：

/*header*/

#include <iostream>

#include <cstdio>

#include <cstring>

#include <algorithm>

#include <queue>

#include <vector>

#include <cmath>

#define rep(i , x, p) for(int i = x;i <= p;++ i)

#define sep(i , x, p) for(int i = x;i >= p;-- i)

#define gc getchar()

#define pc putchar

#define ll long long

#define mk make_pair

#define fi first

#define se second

using std::min;

using std::max;

using std::swap;

const int inf = 0x3f3f3f3f;

const int maxN = 5000 + 7;

const int maxM = 200000 + 7;

inline int gi() {

    int x = 0,f = 1;char c = gc;

    while(c < '0' || c > '9') {if(c == '-')f = -1;c = gc;}

    while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = gc;}return x * f;

}

struct Node {

	int u , v, w;

}Map[maxM];

int n , m;

int f[maxN];

bool vis[maxM];//该边是否用过

int d[maxN] , a[maxN];//各子树的最小连外边的权值

int id[maxN];// 记录各子树的最小连外边的编号 

int find(int x) {return f[x] == x ? x : f[x] = find(f[x]);}

int unqie(int x , int y) {f[find(x)] = find(y);}

int Boruvka() {

	for(int i = 1;i <= n;++ i) f[i] = i;

	int sum = 0;

	while(true) {

		bool flag = false;

		for(int i = 1;i <= n;++ i) d[i] = inf;

		for(int i = 1;i <= m;++ i) {

			int u = find(Map[i].u) , v = find(Map[i].v), c = a[u] & a[v];

			if(u == v) continue;

			flag = true;

			if(c < d[u] || (d[u] == c && id[u] > i)) id[u] = i , d[u] = c;

			if(c < d[v] || (d[v] == c && id[v] > i)) id[v] = i , d[v] = c;

		}

		if(!flag) break;

		for(int i = 1;i <= n;++ i) {

			if(d[i] != inf && !vis[id[i]])  {

				unqie(Map[id[i]].u , Map[id[i]].v);

				sum += Map[id[i]].w;

				vis[id[i]] = true;

			}

		}

	}

	int tot = 0;

	for(int i = 1;i <= n;++ i) if(f[i] == i) tot ++;

	tot > 1 ? printf("orz") : printf("%d",sum);

}

int main() {

	n = gi();m = gi();

	for(int i = 1;i <= m;++ i) {

		int u = gi() , v = gi(), w = gi();

		Map[i] = (Node) {u , v, w};

	}

	Boruvka();

	return 0;

}

CF888G

建造Trie，合并Trie树。