leetcode每日一题：监控二叉树

引言

​ 今天的每日一题原题是2643. 一最多的行，直接模拟，切除和最大的一行即可。更换成前几天遇到的更有意思的一题来写这个每日一题。

题目

968. 监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

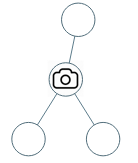
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

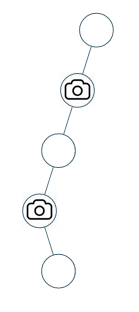
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

1. 给定树的节点数的范围是 [1, 1000]。
2. 每个节点的值都是 0。

思路

​ 我们要放置最少的摄像头，就要让每个摄像头都可以尽可能多的监控到节点。贪心的看，我们不应该在任何一个叶子节点放置摄像头。原因是，如果有一种最优解是在叶子节点放置摄像头，那么我去掉这个摄像头，放置在这个叶子节点的父节点，监控到的范围会比在叶子节点的摄像头范围更广，明显是更优的做法。

​ 有个上面这个大逻辑，我们可以根据每个节点上有无摄像头、以及有无监控分成3种状态（两两组合是4种，但是不可能出现有摄像头无监控，所以实际上是3种）：

• 0：无摄像头，无监控
• 1：无摄像头，有监控
• 2：有摄像头，有监控

对整棵树自下而上来看，根据左右子节点来决策当前节点的状态。

​ 空节点肯定是无摄像头，但是到底有无监控呢？根据我们一开始贪心得到的逻辑，我们不可能在叶子节点放置摄像头，由于空节点可以看到是叶子节点的子节点，所以，我们把空节点状态定义成1：无摄像头，有监控，有利于我们进行递归；

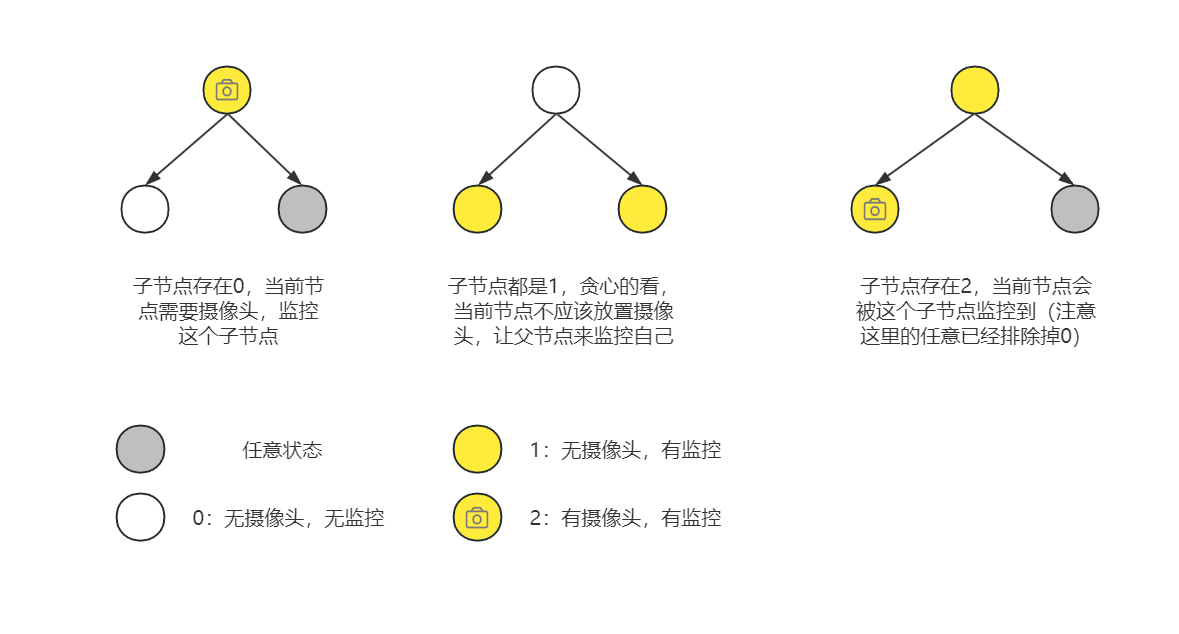
​ 如果左子节点或者右子节点的状态是0：无摄像头，无监控，那么当前节点必须放置摄像头，来监控这个状态为0的子节点，当前节点状态为2：有摄像头，有监控；

​ 如果左子节点和右子节点都是1：无摄像头，有监控，那么当前节点不需要放置摄像头，且不会被某个子节点的摄像头监控到，当前节点状态是0：无摄像头，无监控；

​ 如果左子节点或者右子节点有摄像头（排除掉某个子节点状态是0，上面已经讨论过了），此时当前节点会被这个子节点的摄像头监控到，当前节点的状态是1：无摄像头，有监控

​ 总结一下，当前节点的2个子节点，每个子节点可能有3种状态，排列后一共可能存在9种情况：

null: cur = 1
left = 0 || right = 0, 5种情况, cur = 2, ans++
left = 1, right = 1, 1种情况, cur = 0
left = 2 || right = 2, 3种情况, cur = 1

图解

代码

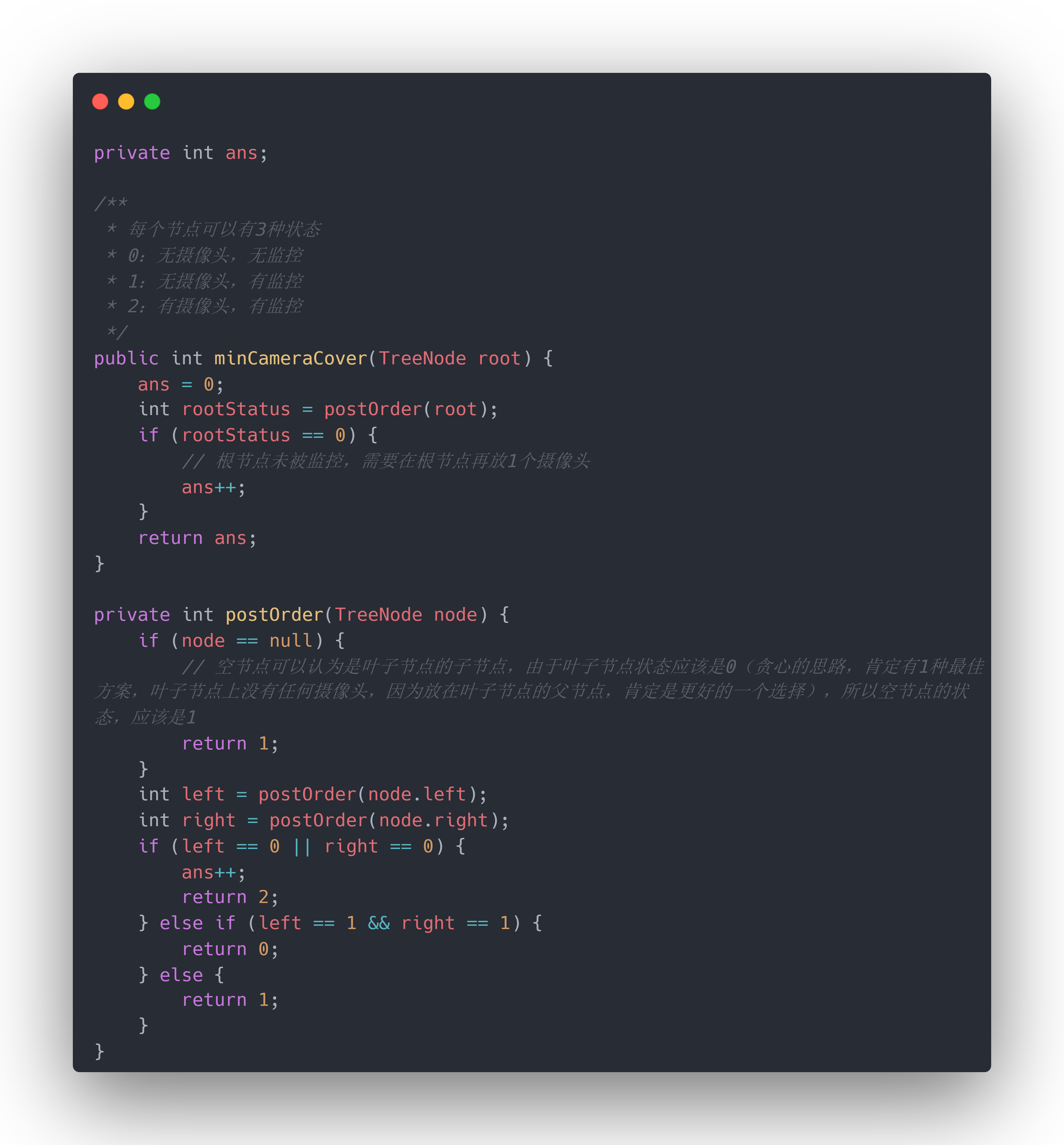
private int ans;
/**
 * 每个节点可以有3种状态
 * 0：无摄像头，无监控
 * 1：无摄像头，有监控
 * 2：有摄像头，有监控
 */
public int minCameraCover(TreeNode root) {
    ans = 0;
    int rootStatus = postOrder(root);
    if (rootStatus == 0) {
        // 根节点未被监控，需要在根节点再放1个摄像头
        ans++;
    }
    return ans;
}
private int postOrder(TreeNode node) {
    if (node == null) {
        // 空节点可以认为是叶子节点的子节点，由于叶子节点状态应该是0（贪心的思路，肯定有1种最佳方案，叶子节点上没有任何摄像头，因为放在叶子节点的父节点，肯定是更好的一个选择），所以空节点的状态，应该是1
        return 1;
    }
    int left = postOrder(node.left);
    int right = postOrder(node.right);
    if (left == 0 || right == 0) {
        ans++;
        return 2;
    } else if (left == 1 && right == 1) {
        return 0;
    } else {
        return 1;
    }
}

耗时