在一个 2^k * 2^k 个方格组成的棋盘中，若恰有一个方格与其他方格不同。则称该方格为一特殊方格，称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对不论什么 k>=0 。有 4^k 种不同的特殊棋盘。

下图所看到的的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。

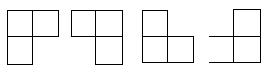
在棋盘覆盖问题中，要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的全部方格，且不论什么 2 个 L 型骨牌不得重叠覆盖。

易知，在不论什么一个 2^k * 2^k 的棋盘中，用到的 L 型骨牌个数恰为 (4^k-1)/3 。

用分治策略，能够设计解棋盘问题的一个简捷的算法。

当 k>0 时，将 2^k * 2^k 棋盘切割为 4 个 2^(k-1) * 2^(k-1) 子棋盘，例如以下图所看到的。

特殊方格必位于 4 个较小子棋盘之中的一个中，其余 3 个子棋盘中无特殊方格。

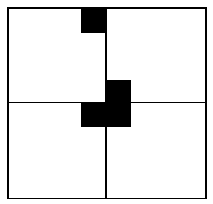
为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘，我们能够用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处。例如以下图所看到的。这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将原问题化为 4 个较小规模的棋盘覆盖问题。递归的使用 这样的切割。直至棋盘简化为 1x1 棋盘。

附代码：

  1. <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN">
  2. <HTML>
  3.  <HEAD>
  4.   <TITLE> New Document </TITLE>
  5.   <META NAME="Generator" CONTENT="EditPlus">
  6.   <META NAME="Author" CONTENT="">
  7.   <META NAME="Keywords" CONTENT="">
  8.   <META NAME="Description" CONTENT="">
  9.   <script type="text/javascript" src="jquery-1.7.2.min.js"></script>
  10.   <script type="text/javascript" src="json2.js"></script>
  11.   <style>
  12.   table,td{
  13.     border:1px solid gray;
  14. 	text-align:center;
  15. 	color:white;
  16.   }
  17.   </style>
  18.   <script>
  19.      var t=0;
  20. 	 var color_arr=['red','yellow','green','blue','purple','orange','pink'];
  21.       var num
  22. 	 function initTable(){
  23. 	    $("#container").html('');
  24. 		var table=$("<table></table>");
  25. 		   num=Math.pow(2,parseInt($("#txt_k").val()));
  26. 		var width=document.body.clientWidth*0.4/num;
  27. 		for(var i=0;i<num;i++){
  28. 		   var tr=$("<tr style='width:"+width*num+"px;height:"+width+"px;'></tr>");
  29. 		   for(var j=0;j<num;j++){
  30. 		     var td=$("<td style='width:"+width+"px;height:"+width+"px;'> </td>");
  31. 			 if(i==parseInt($("#txt_x").val())-1&&j==parseInt($("#txt_y").val())-1)
  32. 			    td.css("background-color","black");
  33. 			 tr.append(td);
  34. 		   }
  35. 		   table.append(tr);
  36. 		}
  37. 		 $("#container").append(table);
  38. 	 }
  39.  
  40. 	 function calcTable(){
  41. 	    var dr=parseInt($("#txt_x").val())-1;
  42. 		var dc=parseInt($("#txt_y").val())-1;
  43. 		t=0;
  44. 	    chessBoard(0,0,dr,dc,num);
  45. 	 }
  46.  
  47. 	 //tr tc子棋盘左上角坐标 dr dc特殊格子坐标 size子棋盘格子数
  48. 	 function chessBoard(tr,tc,dr,dc,size){
  49. 	   var s,t1;
  50. 	   if(size==1)
  51. 	      return;
  52. 		t1=++t;
  53. 		s=size/2;
  54. 		var color=color_arr[t1%color_arr.length];
  55. 		//-------------左上角子棋盘-----------------
  56.         if(dr<tr+s&&dc<tc+s){
  57. 		    //特殊格子在右上角,递归处理子棋盘
  58. 			chessBoard(tr,tc,dr,dc,s);
  59. 		}else{
  60. 		    //处理右下角环绕切割点的棋盘
  61. 			//标记特殊棋盘
  62. 			$("table tr").eq(tr+s-1).find("td").eq(tc+s-1).text(t1);
  63. 			$("table tr").eq(tr+s-1).find("td").eq(tc+s-1).css("background-color",color);
  64. 			chessBoard(tr,tc,tr+s-1,tc+s-1,s);
  65. 		}
  66.  
  67. 		//--------------右上角棋盘-------------------
  68. 		if(dr>=tr+s&&dc<tc+s){
  69. 		   chessBoard(tr+s,tc,dr,dc,s);
  70. 		}else{
  71. 		    //左下角格子
  72. 			$("table tr").eq(tr+s).find("td").eq(tc+s-1).text(t1);
  73. 		    $("table tr").eq(tr+s).find("td").eq(tc+s-1).css("background-color",color);
  74. 			chessBoard(tr+s,tc,tr+s,tc+s-1,s);
  75. 		}
  76. 		//--------------左下角棋盘-------------------
  77. 		if(dr<tr+s&&dc>=tc+s){
  78. 		   chessBoard(tr,tc+s,dr,dc,s);
  79. 		}else{
  80. 		    $("table tr").eq(tr+s-1).find("td").eq(tc+s).text(t1);
  81. 		    $("table tr").eq(tr+s-1).find("td").eq(tc+s).css("background-color",color);
  82. 			chessBoard(tr,tc+s,tr+s-1,tc+s,s);
  83. 		}
  84. 		//--------------右下角棋盘-------------------
  85. 		if(dr>=tr+s&&dc>=tc+s){
  86. 		   chessBoard(tr+s,tc+s,dr,dc,s);
  87. 		}else{
  88. 			//setTimeout("setColor("+tr+s+","+tc+s+",'"+color+"')",1000);
  89. 			$("table tr").eq(tr+s).find("td").eq(tc+s).text(t1);
  90. 		    $("table tr").eq(tr+s).find("td").eq(tc+s).css("background-color",color);
  91. 			chessBoard(tr+s,tc+s,tr+s,tc+s,s);
  92. 		}
  93.  
  94. 	 }
  95.  
  96.   </script>
  97.  </HEAD>
  98.  <BODY style="text-align:center">
  99.      <div>
  100. 	    级数:
  101. 	    <input type="text" id="txt_k"/>
  102.         坐标X：
  103. 		<input type="text" id="txt_x"/>
  104.         坐标Y:
  105. 		<input type="text" id="txt_y"/>
  106. 		<input type="button" id="btn" value="初始化表格" onclick="initTable()"/>
  107. 		<input type="button" id="btn" value="開始棋盘覆盖" onclick="calcTable()"/>
  108. 	 </div>
  109. 	 <div id='container' style="margin:0 auto;">
  110. 	 </div>
  111.  </BODY>
  112. </HTML>

js算法：分治法-棋盘覆盖的更多相关文章

  1. Java算法——分治法

         一.基本概念 在计算机科学中,分治法是一种很重要的算法.字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简 ...

  2. [C++] 分治法之棋盘覆盖、循环赛日程表

    一.分治的基本思想 将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之. 对于一个规模为 n 的问题,若问题可以容易地解决,则直接解决,否则将其分解为 k 个规模较小的子 ...

  3. js算法：分治法-循环赛事日程表

    watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQv/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/ ...

  4. Leedcode算法专题训练（分治法）

    归并排序就是一个用分治法的经典例子,这里我用它来举例描述一下上面的步骤: 1.归并排序首先把原问题拆分成2个规模更小的子问题. 2.递归地求解子问题,当子问题规模足够小时,可以一下子解决它.在这个例子 ...

  5. 算法与数据结构基础 - 分治法(Divide and Conquer)

    分治法基础 分治法(Divide and Conquer)顾名思义,思想核心是将问题拆分为子问题,对子问题求解.最终合并结果,分治法用伪代码表示如下: function f(input x size ...

  6. 《github一天一道算法题》：分治法求数组最大连续子序列和

    看书.思考.写代码. /*************************************** * copyright@hustyangju * blog: http://blog.csdn. ...

  7. 算法笔记_065:分治法求逆序对（Java）

    目录 1 问题描述 2 解决方案 2.1 蛮力法 2.2 分治法(归并排序)   1 问题描述 给定一个随机数数组,求取这个数组中的逆序对总个数.要求时间效率尽可能高. 那么,何为逆序对? 引用自百度 ...

  8. 分治法 - Divide and Conquer

    在计算机科学中,分治法是一种很重要的算法.分治法即『分而治之』,把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的 ...

  9. bzoj 2706: [SDOI2012]棋盘覆盖 Dancing Link

    2706: [SDOI2012]棋盘覆盖 Time Limit: 10 Sec  Memory Limit: 256 MBSubmit: 255  Solved: 77[Submit][Status] ...

随机推荐

  1. tomcat为什么要禁用session？

    转载请标明出处:http://blog.csdn.net/goldenfish1919/article/details/47829755 我们先来做一个实验,用jmeter对tomcat下的一个jsp ...

  2. [IOI 1998] Polygon

    [题目链接] http://poj.org/problem?id=1179 [算法] 区间DP [代码] #include <algorithm> #include <bitset& ...

  3. 2017第33周四JDK8并发

    Java 8在Lambda表达式.接口默认方式.新的日期API等方面引入的新特性广受关注,同时在并发编程方面也做出了大量改进.以往的几个Java版本都对java.util.concurrent做了不同 ...

  4. bfs初学

    BFS: ** 当知道初始和目标状态的,用双向BFS: 无权图最好用BFS 不用重复如队** 实现框架: 抄来的(来源:https://www.luogu.org/blog/stephen2333/s ...

  5. 继承TabActivity后不执行onBackPressed()里的方法

    // 用下面这个函数拦截子Activity的返回操作        @Override        public boolean dispatchKeyEvent(KeyEvent event) { ...

  6. Oracle 新手语法记录

    一.用户 1. 创建用户 语法:create user 用户名 identified by 口令; create user test identified by test; 2. 修改用户 语法:al ...

  7. SQL Server-聚焦移除Bookmark Lookup、RID Lookup、Key Lookup提高SQL查询性能

      前言 前面几节都是讲的基础内容,本节我们讲讲索引性能优化,当对大数据进行处理时首先想到的就是索引,一旦遇到这样的问题则手忙脚乱,各种查资料,为何平常不扎实基本功呢,我们由浅入深,简短的内容,深入的 ...

  8. vue中插件的使用

    <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...

  9. 【转】javascript 小数乘法结果错误处理

    一.用js计算 12.32 * 7  结果是多少? 答案:86.24000000000001   为什么会出现这种问题?怎么解决? js在处理小数的乘除法的时候有一个bug,解决的方法可以是:将小数变 ...

  10. cache（缓存）的作用

    cache的作用: 连接文件.内存与应用,为信息流在三者之间流动提供通道: 存储管理:对外与对内: 存取效率: 多线程: 一次存储:分批存储? 系统的缓存控制机制(虚拟内存)使用分段分页与命中机制. ...