BZOJ1009: [HNOI2008]GT考试(KMP+矩阵乘法)

Description

　　阿申准备报名参加GT考试，准考证号为N位数X1X2....Xn(0<=Xi<=9),他不希望准考证号上出现不吉利的数字。
他的不吉利数学A1A2...Am(0<=Ai<=9)有M位，不出现是指X1X2...Xn中没有恰好一段等于A1A2...Am. A1和X1可以为
0

Input

　　第一行输入N,M,K.接下来一行输入M位的数。 N<=10^9,M<=20,K<=1000

Output

　　阿申想知道不出现不吉利数字的号码有多少种，输出模K取余的结果.

Sample Input

4 3 100
111

Sample Output

81

解题思路：

首先，确定一下什么样的数字中没有不吉利数字。

1.这个数字的前缀不是不吉利数字（废话）

2.这个数字中间不包含不吉利数字（废话）

3.这个数字的后缀不是不吉利数字（废话）

那么，这个数字如果是像汉堡那样一层一层堆的话，我们可以通过尽可能阻止不吉利数字出现来完成任务。

假设数字串出现到了第 i 位，只要后缀m-1位不是不吉利数字m-1位就可以。

所以设f[i][j]为数字堆积到 i 而匹配出来了 j 位。

那么 ：

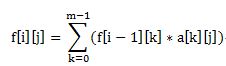
a[k][j]为预处理出来的结果，其概念为：

原串中匹配到 j 时 k 位是否可以被枚举，由于做到不重不漏地计数，每次取前一个next即可

最后由于运算简单但递推长度大，使用矩阵乘法即可。

代码：

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 typedef long long lnt;
 int n,m;
 lnt K;
 char num[];
 int nxt[];
 struct squ{
     lnt s[][];
     squ friend operator * (squ x,squ y)
     {
         squ ans;
         for(int i=;i<m;i++)
         {
             for(int j=;j<m;j++)
             {
                 ans.s[i][j]=;
                 for(int k=;k<m;k++)
                 {
                     ans.s[i][j]=(ans.s[i][j]+x.s[i][k]*y.s[k][j])%K;
                 }
             }
         }
         return ans;
     }
     squ friend operator ^ (squ x,lnt y)
     {
         squ ans=x;
         y--;
         while(y)
         {
             if(y&)
                 ans=ans*x;
             x=x*x;
             y=y/;
         }
         return ans;
     }
 }f,g;
 int main()
 {
     scanf("%d%d%lld",&n,&m,&K);
     scanf("%s",num+);
     nxt[]=nxt[]=;
     for(int i=,j=;i<=m;i++)
     {
         while(j&&num[i]!=num[j+])
             j=nxt[j];
         if(num[i]==num[j+])
             j++;
         nxt[i]=j;
     }
     for(int k=;k<m;k++)
     {
         for(int j=;j<;j++)
         {
             int i=k;
             while(i&&num[i+]!=j+'')
                 i=nxt[i];
             if(num[i+]==j+'')
                 i++;
             if(i!=m)
                 g.s[i][k]=(g.s[i][k]+)%K;
         }
     }
     f=g^n;
     lnt ans=;
     for(int i=;i<m;i++)
     {
         ans=(ans+f.s[i][])%K;
     }
     printf("%lld\n",ans);
     return ;
 }