Codeforces 757 D. Felicity's Big Secret Revealed 状压DP

D. Felicity's Big Secret Revealed

 

The gym leaders were fascinated by the evolutions which took place at Felicity camp. So, they were curious to know about the secret behind evolving Pokemon.

The organizers of the camp gave the gym leaders a PokeBlock, a sequence of n ingredients. Each ingredient can be of type 0 or 1. Now the organizers told the gym leaders that to evolve a Pokemon of type k (k ≥ 2), they need to make a valid set of k cuts on the PokeBlock to get smaller blocks.

Suppose the given PokeBlock sequence is b0b1b2... bn - 1. You have a choice of making cuts at n + 1 places, i.e., Before b0, between b0 and b1, between b1 and b2, ..., between bn - 2 and bn - 1, and after bn - 1.

The n + 1 choices of making cuts are as follows (where a | denotes a possible cut):

| b0 | b1 | b2 | ... | bn - 2 | bn - 1 |

Consider a sequence of k cuts. Now each pair of consecutive cuts will contain a binary string between them, formed from the ingredient types. The ingredients before the first cut and after the last cut are wasted, which is to say they are not considered. So there will be exactly k - 1 such binary substrings. Every substring can be read as a binary number. Let m be the maximum number out of the obtained numbers. If all the obtained numbers are positive and the set of the obtained numbers contains all integers from 1 to m, then this set of cuts is said to be a valid set of cuts.

For example, suppose the given PokeBlock sequence is 101101001110 and we made 5 cuts in the following way:

10 | 11 | 010 | 01 | 1 | 10

So the 4 binary substrings obtained are: 11, 010, 01 and 1, which correspond to the numbers 3, 2, 1 and 1 respectively. Here m = 3, as it is the maximum value among the obtained numbers. And all the obtained numbers are positive and we have obtained all integers from 1 to m. Hence this set of cuts is a valid set of 5 cuts.

A Pokemon of type k will evolve only if the PokeBlock is cut using a valid set of k cuts. There can be many valid sets of the same size. Two valid sets of k cuts are considered different if there is a cut in one set which is not there in the other set.

Let f(k) denote the number of valid sets of k cuts. Find the value of 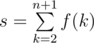. Since the value of s can be very large, output smodulo 109 + 7.

Input

The input consists of two lines. The first line consists an integer n (1 ≤ n ≤ 75) — the length of the PokeBlock. The next line contains the PokeBlock, a binary string of length n.

Output

Output a single integer, containing the answer to the problem, i.e., the value of s modulo 109 + 7.

Examples

input

4
1011

output

10

 

Note

In the first sample, the sets of valid cuts are:

Size 2: |1|011, 1|01|1, 10|1|1, 101|1|.

Size 3: |1|01|1, |10|1|1, 10|1|1|, 1|01|1|.

Size 4: |10|1|1|, |1|01|1|.

Hence, f(2) = 4, f(3) = 4 and f(4) = 2. So, the value of s = 10.

In the second sample, the set of valid cuts is:

Size 2: |1|0.

Hence, f(2) = 1 and f(3) = 0. So, the value of s = 1.

题意：

　　给定一个01串，一个有效的n切割定义如下：竖杠代表切割线，第一条竖杠前面的01串忽略，最后一条竖杠后面的01串忽略，将相邻竖杠夹住的01串转化成十进制数字

　　假设这些数字的最大值是m且这些数字囊括了1-m的所有数字，则称为一次有效切割。

　　问你方案数

题解：

　　dp[i][j] 表示以i结尾的01串中所能涵括的数状态为j的方案

　　那么 dp[k][j|(1<<(x-1))] += dp[i][j] （i+1 <= k <= n） x为i+1到k这串的十进制数

　　暴力转移统计答案

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<int,int>
#define MP make_pair
typedef long long LL;
const long long INF = 1e18+1LL;
const double Pi = acos(-1.0);
const int N = +, M = 1e3+, mod = 1e9+, inf = 2e9;
int dp[N][(<<) + ];
int a[N],n;
char s[N];
int main() {
    scanf("%d%s",&n,s+);
    for(int i = ; i <= n; ++i) a[i] = s[i] - '';
    for(int i = ; i <= n; ++i) {
        dp[i][] = ;
        for(int j = ; j < (<<); ++j) {
            if(dp[i][j]) {
                LL x = ;
                for(int k = i+; k <= n; ++k) {
                    x += a[k];
                    if(x > ) break;
                    if(!x) continue;
                    dp[k][j|(<<(x-))] += dp[i][j];
                    dp[k][j|(<<(x-))] %= mod;
                    x *= ;
                }
            }
        }
    }
    LL ans = ;
    for(int i = ; i <= n; ++i) {
        for(int j = ; j <= ; ++j) ans = (ans + dp[i][(<<j)-])%mod;
    }
    cout<<ans<<endl;
    return ;
}