caj转pdf——包含下载链接
很多人在知网上下载论文后,想转换成PDF格式,本片一站式教学,包含下载链接。
需要工具
1 caj格式的文件,即要转换的文件。
2 cajviewer,可以在知网的官网上面下载,下载地址参考这里。
3 虚拟打印机,
可以是Adobe acrobat(这个太大了,而且官方需要序列号,不推荐),
或者 TinyPdf(我是64位的系统,官方说是32位有免费的,没有试过),
这里推荐一个64位可用的虚拟打印机。
转换方法
首先,使用cajviewer打开caj文件,按ctrl+p,弹出打印框(如果正确安装上了虚拟打印机,就会出现这个打印选项),选择doro虚拟打印机:
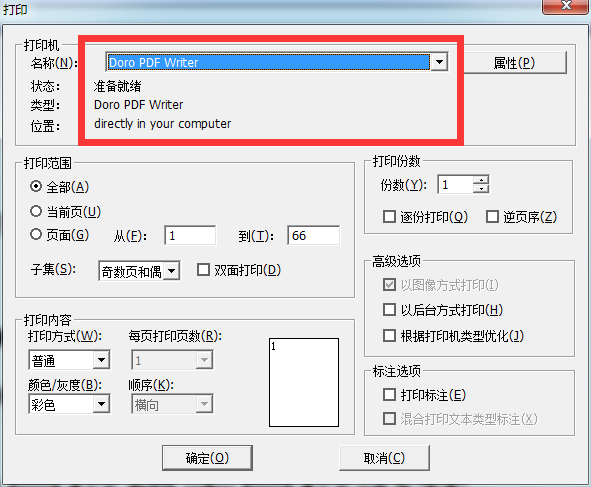
然后选择转换的页码,点击确定:

最后在红色框框位置,填写转换出来的Pdf名字以及导出的目录,点击创建!
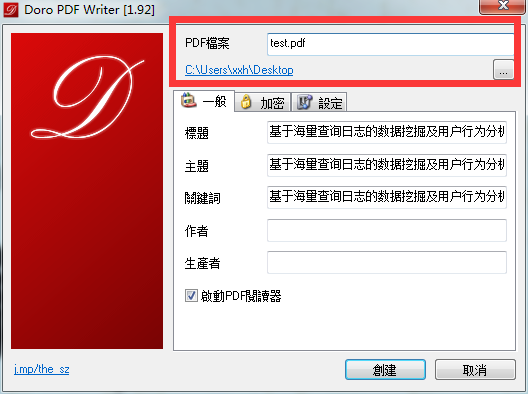
转换成功!
caj转pdf——包含下载链接的更多相关文章
- 《C程序设计语言》【PDF】下载链接:
<C程序设计语言>[PDF]下载 https://u253469.pipipan.com/fs/253469-230382180 内容简介 在计算机发展的历史上,没有哪一种程序设计语言像C ...
- 《精通c#(第6版)》【PDF】下载
图灵程序设计丛书:精通C#(第6版)是C#领域久负盛名的经典著作,深入全面地讲解了C#编程语言和.NET平台的核心内容,并结合大量示例剖析相关概念.全书分为八部分:C#和.NET平台.C#核心编程结构 ...
- 《Head First 设计模式》【PDF】下载
<Head First 设计模式>[PDF]下载链接: https://u253469.ctfile.com/fs/253469-231196307 First 设计模式>[PDF] ...
- 《写给大家看的设计书(第3版)》【PDF】下载
<写给大家看的设计书(第3版)>[PDF]下载链接: https://u253469.ctfile.com/fs/253469-231196355 内容简介 <写给大家看的设计书&g ...
- 《Effective Java(中文第二版)》【PDF】下载
<Effective Java(中文第二版)>[PDF]下载链接: https://u253469.pipipan.com/fs/253469-230382186 Java(中文第二版)& ...
- 《python参考手册(第四版)》【PDF】下载
<python参考手册(第四版)>[PDF]下载链接: https://u253469.pipipan.com/fs/253469-230382222 内容介绍 本书是权威的Python语 ...
- 《程序设计语言——实践之路》【PDF】下载
程序设计语言--实践之路>[PDF]下载链接: https://u253469.pipipan.com/fs/253469-230382240 内容简介 本书在美国大学已有使用了十余年,目前被欧 ...
- 《代码大全(第二版)》【PDF】下载
<代码大全(第二版)>[PDF]下载链接: https://u253469.pipipan.com/fs/253469-230382264 内容简介 <代码大全(第2版)>是著 ...
- 《深入浅出node.js(朴灵)》【PDF】下载
<深入浅出node.js(朴灵)>[PDF]下载链接: https://u253469.pipipan.com/fs/253469-230062563 内容简介 <深入浅出Node. ...
随机推荐
- 没啥用,更换注册表信息使webbrower选择适合的版本
/// <summary> /// 修改注册表信息来兼容当前程序 /// /// </summary> ...
- 109.Convert sorted list to BST
/* * 109.Convert sorted list to BST * 2016.12.24 by Mingyang * 这里的问题是对于一个链表我们是不能常量时间访问它的中间元素的. * 这时候 ...
- LINUX下安装和配置WEBLOGIC10.0.3
weblogic for linux安装 首先声明,我参考了某位原创者的笔记,加以整理的.安装1. 安装前的准备工作1.1 首先请确认您要安装的Weblogic版本所在的平台已通过了BEA的认证,完整 ...
- 常见machine learning模型实现
一.感知机模型 二.线性回归(Linear Regression) from numpy import * def loadData(filename): x = [] y = [] f = open ...
- 【c++】面向对象程序设计之访问控制与继承
受保护的成员(protected): 1.和私有成员类似,受保护的成员对于类的用户来说是不可访问的 2.和共有成员类似,受保护的成员对于派生类的成员和友元来说是可访问的 3.派生类的友元只能通过派生类 ...
- Linux 修改终端命令提示符颜色
相信很多人已经看厌了Linux已成不变的命令提示符的颜色,多数人要么使用默认的绿色,要么在使用PUTTY的时候设置成绿色的,不知道是否有人想到提示符可以设置成其他的颜色呢,本文就说明命令提示符变量PS ...
- Linux上设置RAID 10
RAID 10(又叫RAID 1+0或镜像条带)阵列结合了RAID 0和RAID 1两者的功能特性,从而提供了高性能.容错的磁盘输入/输出操作.在RAID 0中,读取/写入操作跨多个驱动器并路执行:在 ...
- 运行mapreduce - java.lang.InterruptedException
错误日志: 2018-11-19 05:23:51,686 WARN [main] util.NativeCodeLoader (NativeCodeLoader.java:<clinit> ...
- Zookeeper开发常见问题
背景与目的 Zookeeper开发过程中遇到一些常见问题,为了后续开发不犯同样的错误,总结一下此类问题,并进行分析和解决. 适合人员 主要适合zookeeper开发.测试及运维相关人员. 问题与解决 ...
- WEKA简单介绍与资源汇总
简单介绍 Weka是一个开源的数据挖掘软件,里面集成了很多经典的机器学习算法,在高校和科研机构中受到了广泛的应用. 具体的简单介绍和简单的使用请參考文档:<使用Weka进行数据挖掘>. 学 ...
