GT考试 BZOJ 1009

GT考试

【问题描述】

阿申准备报名参加GT考试，准考证号为N位数X1X2....Xn(0<=Xi<=9)，他不希望准考证号上出现不吉利的数字。

他的不吉利数学A1A2...Am(0<=Ai<=9)有M位，不出现是指X1X2...Xn中没有恰好一段等于A1A2...Am. A1和X1可以为0

【输入格式】

第一行输入N,M,K.接下来一行输入M位的数。

【输出格式】

阿申想知道不出现不吉利数字的号码有多少种，输出模K取余的结果.

【样例输入】

4 3 100

111

【样例输出】

81

【数据范围】

N<=10^9， M<=20， K<=1000

---

题解：

设f[i][j]表示至准考证号前i位，最多匹配到不吉利数的第j位的方案数

设a[i][j]表示在不吉利数的前i位后加上一个字符能匹配到不吉利数的第j位的字符的数量（枚举字符用KMP求出a矩阵）

那么转移方程：

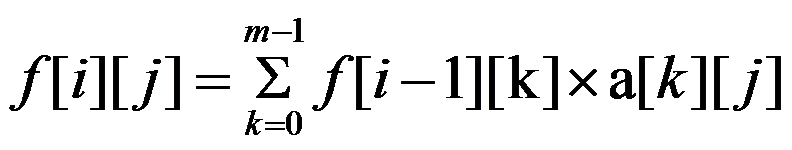
答案：

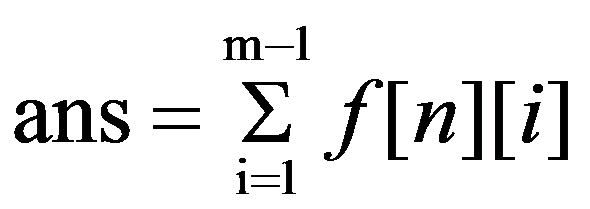
发现转移方程可以用矩阵乘法优化

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 using namespace std;
 int n, m, t, mo, sum, s[], ne[];
 struct ccc
 {
     int v[][];
     ccc()
     {
         memset(v, , sizeof(v));
     }
     friend ccc operator * (ccc a, ccc b)
     {
         ccc ans;
         for(int i = ; i < m; ++i)
             for(int j = ; j < m; ++j)
                 for(int k = ; k < m; ++k)
                     ans.v[i][j] = (ans.v[i][j] + a.v[i][k] * b.v[k][j]) % mo;
         return ans;
     }
     friend ccc operator ^ (ccc a, int b)
     {
         ccc ans;
         for(int i = ; i <= m; ++i) ans.v[i][i] = ;
         for(int i = b; i; i >>= , a = a * a)
             if(i & )
                 ans = ans * a;
         return ans;
     }
 };
 ccc a, c;
 int main()
 {
     scanf("%d%d%d", &n, &m, &mo);
     getchar();
     for(int i = ; i <= m; ++i) s[i] = getchar() - '';
     t = ;
     for(int i = ; i <= m; ++i)
     {
         while(t >  && s[i] != s[t + ]) t = ne[t];
         if(s[i] == s[t + ]) ++t;
         ne[i] = t;
     }
     for(int i = ; i < m; ++i)
         for(int j = ; j <= ; ++j)
         {
             t = i;
             while(t >  && s[t + ] != j) t = ne[t];
             if(s[t + ] == j) ++t;
             if(t != m) a.v[t][i] = (a.v[t][i] + ) % mo;
         }
     for(int i = ; i < m; ++i)
     {
         for(int j = ; j < m; ++j)
             printf("%d ", a.v[i][j]);
         printf("\n");
     }
     c = a ^ n;
     for(int i = ; i < m; ++i) sum = (sum + c.v[i][]) % mo;
     printf("%d", sum);
 }