【HIHOCODER 1605】小Hi的生成树计数

描述

---

小Hi最近对生成树（包含所有顶点的联通无环子图。）非常的感兴趣，他想知道对于特定的简单平面无向图是不是存在求生成树个数的简单方法。

小Hi定义了这样的图：一个以{0，1，2……n}为顶点的图，顶点0与其他n个顶点直接相连，对于顶点i（1 ≤ i < n），顶点i与顶点i+1连有一条边。下面是小Hi画的图n=4的图：

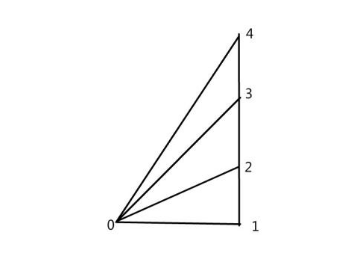
请求出对于任意n,这样的图的生成树个数。

输入

---

多组数据，每组数据一行，包括一个整数n

30%的数据（1 ≤ n ≤ 100），组数不超过10组

70%的数据（1 ≤ n ≤ 1000000），组数不超过10组

100%的数据（1 ≤ n ≤ 1000000000）,组数不超过10组

输出

---

每组数据输出一个行包括一个整数，代表了图的生成树个数（对1000000007取模）。

样例输入

2

样例输出

3

题解

---

套用矩阵树定理的板子，输出前几项发现是斐波那契数列的偶数项，即ans(n)=f(2n)

#include <vector>
#include <queue>
#include <cstdio>
#include <complex>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ll long long
#define inf 1000000000
#define PI acos(-1)
#define bug puts("here")
#define REP(i,x,n) for(int i=x;i<=n;i++)
#define DEP(i,n,x) for(int i=n;i>=x;i--)
#define mem(a,x) memset(a,x,sizeof(a))
typedef unsigned long long ull;
using namespace std;
inline int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline void Out(int a){
    if(a<0) putchar('-'),a=-a;
    if(a>=10) Out(a/10);
    putchar(a%10+'0');
}
const int MOD=1000000007;
const int tn=2;
struct Matrix
{
    ll m[111][111];
    Matrix()
    {
        memset(m,0,sizeof(m));
    }
    friend Matrix operator*(Matrix a,Matrix b)
    {
        Matrix res;
        ll x;
        for(int i=0; i<tn; i++)
        {
            for(int j=0; j<tn; j++)
            {
                x=0;
                for(int k=0; k<tn; k++)
                {
                    x=(x+(ll)a.m[i][k]*b.m[k][j])%MOD;
                }
                res.m[i][j]=x;
            }
        }
        return res;
    }
    friend Matrix operator^(Matrix a,int b)
    {
        Matrix ans;
        for(int i=0;i<tn;i++) ans.m[i][i]=1;
        for(int i=b; i; i>>=1,a=a*a)
            if(i&1)ans=ans*a;
        return ans;
    }
};
int main(){
    int n;
    while(~scanf("%d",&n))
    {
          Matrix res,base;
          base.m[0][0]=base.m[0][1]=base.m[1][0]=1;
          base.m[1][1]=0;
          res=base^(2*n);
          printf("%lld\n",res.m[1][0]%MOD);
    }
    return 0;
}