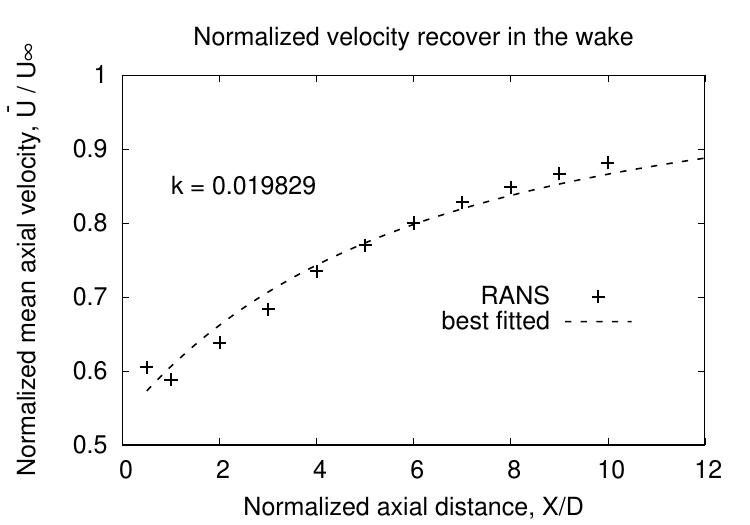
k fit in Park Model

software: Gnuplot

input: area_averaged_axial_mean_velocity_TI_1.txt

# One Rotor, front, eldad blade
# TSR , TI =%
#X/D    X   half width,    Ux    U    Ux/U
0.5    0.23    0.275    0.363    0.6    0.605
    0.46    0.93    0.353    0.6    0.588333333
    0.92    0.316    0.383    0.6    0.638333333
    1.38    0.334    0.41    0.6    0.683333333
    1.84    0.349    0.441    0.6    0.735
    2.3    0.365    0.462    0.6    0.77
    2.76    0.379    0.48    0.6    0.8
    3.22    0.39    0.497    0.6    0.828333333
    3.68    0.405    0.509    0.6    0.848333333
    4.14    0.42    0.52    0.6    0.866666667
    4.6    0.431    0.529    0.6    0.881666667

gnuplot code

a = 0.6*(1-sqrt(1-0.7133))
d=0.46
f(x) = (0.6-a*d*d/((d+2*k*x)*(d+2*k*x)))/0.6
fit f(x) 'area_averaged_axial_mean_velocity_TI_1.txt' using 1:6 via k
# plotting
set terminal postscript eps font 24
set out 'k_fit_ti_1_tsr5.eps'
set autoscale
unset log
unset label
unset pm3d
set xtic auto
set ytic auto
unset grid
# set title 'Normalized velocity recover in the wake'
set xlabel  "Normalized axial distance, X/D"
set xrange [*:12]
# r0 initial pulse
set yrange [0.5:1]
set ylabel "Normalized mean axial velocity, ~U{0.8-} / U{/Symbol \245}"
set style line 1 lt 1 lc rgb "black" lw 4 pt 1 ps 2
set style line 2 lt 2 lc rgb "black" lw 4  pt 3 ps 2
set style line 3 lt 3 lc rgb "black" lw 4  pt 5 ps 2
set style line 4 lt 4 lc rgb "black" lw 4  pt 7 ps 2
set style line 5 lt 5 lc rgb "black" lw 4
set style line 6 lt 6 lc rgb "brown" lw 4
k_value = sprintf("k = %.3f", k)
set label 1 at 1, 0.85  k_value
set key at graph 0.9, 0.3
set key spacing 1
plot 'area_averaged_axial_mean_velocity_TI_1.txt' using 1:6 ls 1 with points title 'RANS', f(x) lw 3 title "best fitted"

output: