《算法竞赛进阶指南》1.6Trie

142. 前缀统计

给定N个字符串S1,S2…SN，接下来进行M次询问，每次询问给定一个字符串T，求S1～SN中有多少个字符串是T的前缀。

输入字符串的总长度不超过106，仅包含小写字母。

输入格式

第一行输入两个整数N，M。

接下来N行每行输入一个字符串Si。

接下来M行每行一个字符串T用以询问。

输出格式

对于每个询问，输出一个整数表示答案。

每个答案占一行。

输入样例：

3 2

ab

bc

abc

abc

efg

输出样例：

2

0

#include <iostream>

using namespace std;

const int N = 1000010, M = 500000; //trie 的长度

int n, m;
int son[M][26], cnt[N], idx; //cnt记录该节点是多少个字符串的末尾节点 idx 虚拟内存的指针(当前用到的数组的地址，当前节点的下标)
char str[N];

int query() //查询 字符串前缀个数
{
    int p = 0, res = 0; //res 表示当前路径所有单词的总和
    for(int i = 0; str[i]; i++)
    {
        int &s = son[p][str[i] - 'a'];
        if(!s) break; //当前节点为空 没有下面的路径 break
        p = s;
        res += cnt[p]; //加上以当前节点为结尾的个数
    }
    return res;
}

void insert() //插入
{
    int p = 0; //trie根节点  0号节点
    for(int i = 0; str[i]; i++)
    {
        int &s = son[p][str[i] - 'a']; //当前儿子
        if(!s) s = ++ idx; //s 不存在 分配一个新的值
        p = s;
    }
    cnt[p] ++; //有一个单词以p节点为结尾 加1
}

int main()
{
    scanf("%d%d", &n, &m); //输入规模大于100万用scanf()

    while(n --)
    {
        scanf("%s", str);
        insert();
    }

    while(m --)
    {
        scanf("%s", str);
        printf("%d\n", query());
    }
    return 0;
}

143. 最大异或对

在给定的N个整数A1，A2……AN中选出两个进行xor（异或）运算，得到的结果最大是多少？

输入格式

第一行输入一个整数N。

第二行输入N个整数A1～AN。

输出格式

输出一个整数表示答案。

数据范围

1≤N≤105,

0≤Ai<231

输入样例：

3

1 2 3

输出样例：

3

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010, M = 3000000; //M节点个数

int n;
int son[M][2],idx;
int a[N];

void insert(int x)
{
    int p = 0;
    for(int i = 30; ~i; i--) //i >= 0 等价于 ~i
    {
        int &s = son[p][x >> i & 1]; //取出二进制第i位 看第i位是0还是1
        if(!s) s = ++ idx; //创建新节点
        p = s;
    }
}

int query(int x)
{
    int res = 0, p = 0;
    for(int i = 30; ~i; i--)
    {
        int s = x >> i & 1;
        if(son[p][!s]) //查看不一样的分支是否存在 1看0 0看1
        {
            res += 1 << i; //当前位对res所做出的贡献
            p = son[p][!s];
        }
        else p = son[p][s];
    }
    return res;
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> a[i];
        insert(a[i]);
    }
    int res = 0;
    for(int i = 0; i < n; i++) res = max(res, query(a[i])); //query 找到和当前异或最大的结果

    cout << res << endl;
    return 0;
}

144. 最长异或值路径

给定一个树，树上的边都具有权值。

树中一条路径的异或长度被定义为路径上所有边的权值的异或和：



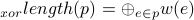
⊕ 为异或符号。

给定上述的具有n个节点的树，你能找到异或长度最大的路径吗？

输入格式

第一行包含整数n，表示树的节点数目。

接下来n-1行，每行包括三个整数u，v，w，表示节点u和节点v之间有一条边权重为w。

输出格式

输出一个整数，表示异或长度最大的路径的最大异或和。

数据范围

1≤n≤100000,

0≤u,v<n,

0≤w<231

输入样例：

4

0 1 3

1 2 4

1 3 6

输出样例：

7

样例解释

样例中最长异或值路径应为0->1->2,值为7 (=3 ⊕ 4)

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 100010, M = 3000000; //M节点个数

int n;
int h[N], e[N * 2], c[N * 2], ne[N * 2], cnt; //树：数组模拟邻接表来存,e无向图,边数*2,c是边权,ne存next指针，cnt内存,当前位下标
int son[M][2],idx;
int a[N];

void add(int u, int v, int w) //把u,v加到图里面去
{
    e[cnt] = v, c[cnt] = w, ne[cnt] = h[u], h[u] = cnt ++; //数组模拟邻接表
}

void dfs(int u, int father, int sum)
{
    a[u] =sum;
    for(int i = h[u]; ~i; i = ne[i]) //遍历u这一点的所有儿子
    {
        int j = e[i]; //j表示儿子
        if( j != father) //这条边的出边不是往上走的
            dfs(j, u, sum ^ c[i]);
    }
}

void insert(int x)
{
    int p = 0;
    for(int i = 30; ~i; i--) //i >= 0 等价于 ~i
    {
        int &s = son[p][x >> i & 1]; //取出二进制第i位 看第i位是0还是1
        if(!s) s = ++ idx; //创建新节点
        p = s;
    }
}

int query(int x)
{
    int res = 0, p = 0;
    for(int i = 30; ~i; i--)
    {
        int s = x >> i & 1;
        if(son[p][!s]) //查看不一样的分支是否存在 1看0 0看1
        {
            res += 1 << i; //当前位对res所做出的贡献
            p = son[p][!s];
        }
        else p = son[p][s];
    }
    return res;
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h); //初始化邻接表表头
    for(int i = 0; i < n - 1; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        add(u, v, w);
        add(v, u, w); //无向图 加两条边
    }

    dfs(0, -1, 0); //从根节点0开始，-1 无向图遍历常用方式 出边等于父节点 不回溯 ,sum 开始为 0

    for(int i = 0; i < n; i++) insert(a[i]); //根节点到i的路径所有边权的xor值

    int res = 0;
    for(int i = 0; i < n; i++) res = max(res, query(a[i])); //query 找到和当前异或最大的结果

    cout << res << endl;
    return 0;
}