文艺平衡树 Splay 学习笔记(1)

（这里是Splay基础操作，reserve什么的会在下一篇里面讲）

好久之前就说要学Splay了，结果苟到现在才学习。

可能是最近良心发现自己实在太弱了，听数学又听不懂只好多学点不要脑子的数据结构。

感觉Splay比Treap良心多了——代码真的好写。

对于Splay显然可以维护Treap的所有操作，并且本质是BST。

先看看Splay是怎么维护普通平衡树操作的吧。

首先先定义一些基础的变量（若不作特殊说明这些变量的意义不变）

int t[N][2] // t[x][0]表示节点x的左子树,t[x][1]表示节点x的右子树

int cnt[N] // cnt[x]表示节点x存储多少个重复的数

int val[N] // val[x]表示节点x存储数的大小

int par[N] // par[x]表示节点x的直接父亲，特别的，根节点的直接父亲为0

int size[N] // size[x]表示在BST中x子树中存储数的个数

# define ls(x) (t[x][0])

# define rs(x) (t[x][1]) //方便书写

初始化：Splay平衡树中有有+无穷 -无穷两个哨兵节点！！！

Check(x) 函数 :

询问节点x是其父亲的左儿子(return 0)还是右孩子(return 1)

int check (int x)  {
    return rs(par[x])==x;
}

由上述代码可知，根节点的check(root)值为0，即根节点是0节点的左儿子(Nothing Special）

Up(x)函数：

对于节点x维护其size值为两个孩子的size值+自身cnt值。

void up(int x){
    size[x]=size[ls(x)]+size[rs(x)]+cnt[x];
}

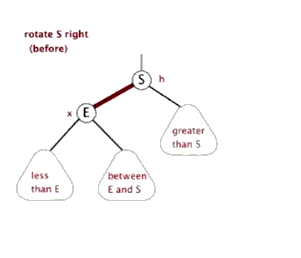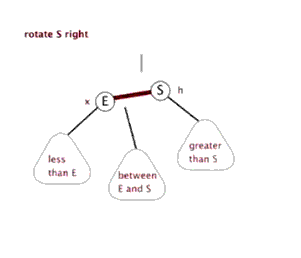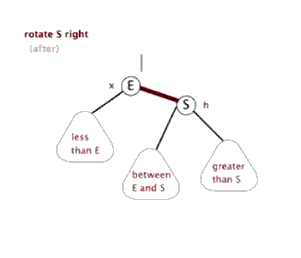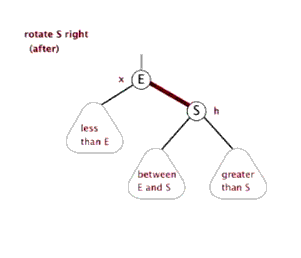
Rotate(x)函数：

对于节点x旋转到其父亲节点，且不改变树BST性质。（使得树形态较为随机）

这里需要解释一下Rotate的解释和记忆方法（和Treap中Rotate类似）

对于一棵有根树（且父亲指向儿子的边有向），我们现在以把左儿子旋到父节点为例。

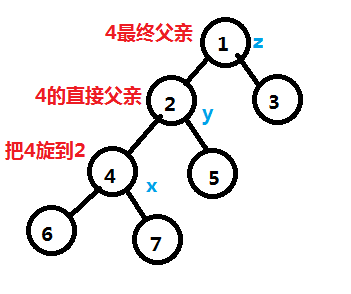
第1步，考虑4的右子树已经有元素了，考虑把右子树连接到父节点左儿子处。不改变BST性质。

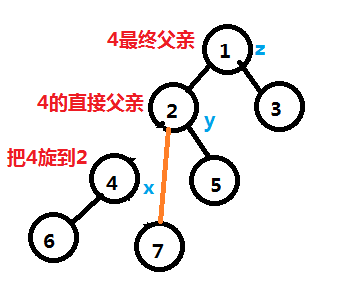
在此基础上考虑第二步，就是吧2（4的直接父亲接到4的右边）不改变BST性质。

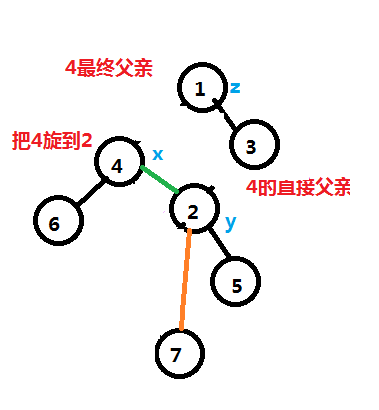
这个时候我们会发现，只进行第三部就可以完成一次rotate操作。

即连一条1指向4的边即可。

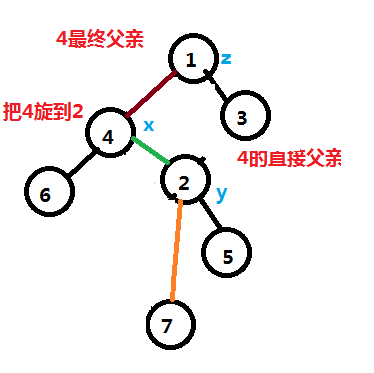
对于左边节点转到父亲节点，一般称之为右旋

对于右旋函数的代码，不难得到。

void rotate(int x){
  int y=par[x];
  t[y][]=t[x][]; par[t[x][]]=y;
  t[x][]=y; t[par[y]][check(y)]=x;
  par[x]=par[y]; par[y]=x;
  up(y); up(x);
}

右旋

那左旋呢？？？

所有0和1的地方去个反不就好了！！！(至少我是那么记的)

对于 真正的旋转代码：

void rotate(int x){
      int y=par[x],k=check(x);
      t[y][k]=t[x][k^]; par[t[x][k^]]=y;
      t[x][k^]=y; t[par[y]][check(y)]=x;
      par[x]=par[y]; par[y]=x;
      up(y); up(x);
}

Splay(x,goal) 操作

把节点x通过若干次rotate操作使其到达目标节点goal或者为根，而goal却成为节点x的儿子。

我们可以分三种情况讨论：

1. goal 是 x的直接父亲（边界），那么直接将x旋到父亲位置即可

2. x和x的直接父亲y和x的爷爷z在同一条直线上(不会打结吗？我们需要给定一种顺序)

那么先旋转父亲y，再旋转x，这个时候想就被旋转到y和z节点上方了。

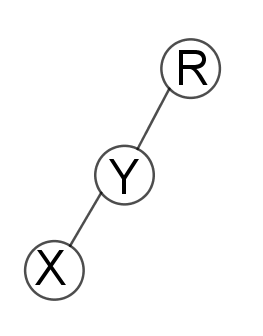
3. x和x的直接父亲y和x的爷爷z在不在同一条直线上（直接把x转两次不就行了么）

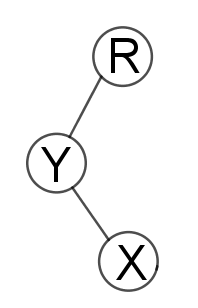
我们可以参考下图，模拟一条链上的Splay操作。

简单的代码实现如下（自然语言是多么的无力....）

void splay(int x,int goal=) {
    while (par[x]!=goal) {
        int y=par[x],z=par[y];
        if (z!=goal) {
            if (check(x)==check(y)) rotate(y);
            else rotate(x);
        }
        rotate(x);
    }
    if (!goal) root=x;
}

Insert(x)操作

插入一个值为x的元素。

显然从根节点开始按照BST性质访问Splay，直到找到一个节点v，其值val[v]恰好为x，那么直接增加个数

如果找不到节点的的val[v]恰好为x，那么新建一个节点即可。

最后Splay一下防止出现长链的情况。

void insert(int x) {
    int cur=root,p=;
    while (cur && val[cur]!=x)
        p=cur,cur=t[cur][x>val[cur]];
    if (cur) cnt[cur]++;
    else {
        cur=++tot;
         if (p) t[p][x>val[p]]=cur;
         ls(cur)=rs(cur)=;
         par[cur]=p; val[cur]=x;
         size[cur]=cnt[cur]=;
     }
      splay(cur);
}

Find(x)函数

将val值小于等于x的val值最大一个节点，旋转到根。

题目解决在于如何找到val值小于等于x的val最大的一个节点，注意不能找到空节点，所以要判断。

找到节点v直接利用Splay操作，旋转到根即可。

void find(int x){
     if (!root) return;
     int cur=root;
     while (t[cur][x>val[cur]] && val[cur]!=x)
          cur=t[cur][x>val[cur]];
     splay(cur);
}

Rank(x)函数

求值x的排名（x可能曾经没有出现过），排名的定义是比x小的元素个数+1。

利用find操作后，如果x之前出现过，即val[root]=x，那么直接输出左子树的size

否则那么根节点一定比x小那么还需要加上根节点的cnt

int rank(int x){
     find(x);
     if (val[root]>=x) return size[ls(root)];
     else return size[ls(root)]+cnt[root]-;
}

pre(x)和suc(x)函数

求值x的前驱(比x小的最大数，若没有是-无穷)，求值x的后继（比x大的最小数，若没有是+无穷），x可能没有出现过。

求前驱，考虑find操作以后小于等于x的元素都在根及根的左侧，那么如果根直接小于x（x之前没出现过），那么直接打印根就行

否则在左子树中找一直往右子树走找最大的即可。

求后继，考虑find操作以后大于等于x的元素都在根及根的左侧，那么如果根直接大于x（x之前没出现过），那么直接打印根就行

否则在右子树中找一直往左子树走找最小的即可。

int pre_id(int x) {
     find(x);
     if (val[root]<x) return root;
     int cur=ls(root);
     while (rs(cur)) cur=rs(cur);
     return cur;
}
int pre_val(int x){
     return val[pre_id(x)];
}
int suc_id(int x) {
     find(x);
     if (val[root]>x) return root;
     int cur=rs(root);
     while (ls(cur)) cur=ls(cur);
     return cur;
}
int suc_val(int x){
      return val[suc_id(x)];
}

erase(x)操作

删除权值为x的一个数。

考虑数x的前驱和后继是唯一的，那么求出x的前驱和x的后继，均用Splay操作转到根节点和根节点的右儿子处，

那么根节点右儿子的左儿子一定就可知道是x的了。直接删除它即可，特别的是，剩余个数大于1和等于1的时候需要不同处理

其中大于1的时候，直接吧cnt减去1即可，等于1的时候，则需要删除节点所有的信息。

void erase(int x){
     int last=pre_id(x),next=suc_id(x);
     splay(last),splay(next,last);
     int d=ls(rs(root));
     if (cnt[d]>) cnt[d]--,splay(d);
     else t[next][]=;
}

Treap模板题目：https://www.luogu.org/problemnew/show/P3369

# include <bits/stdc++.h>
using namespace std;
const int N=2e5+;
struct Splay{
    # define ls(x) (t[x][])
    # define rs(x) (t[x][])
    # define inf (0x3f3f3f3f)
    int t[N][],cnt[N],val[N],size[N],par[N];
    int root,tot;
    Splay() { tot=root=; insert(-inf); insert(inf);}
    int check(int x) { return rs(par[x])==x; }
    void up(int x){
        size[x]=size[ls(x)]+size[rs(x)]+cnt[x];
    }
    void rotate(int x){
        int y=par[x],k=check(x);
        t[y][k]=t[x][k^]; par[t[x][k^]]=y;
        t[x][k^]=y; t[par[y]][check(y)]=x;
        par[x]=par[y]; par[y]=x;
        up(y); up(x);
    }
    void splay(int x,int goal=) {
        while (par[x]!=goal) {
            int y=par[x],z=par[y];
            if (z!=goal) {
                if (check(x)==check(y)) rotate(y);
                else rotate(x);
            }
            rotate(x);
        }
        if (!goal) root=x;
    }
    void insert(int x) {
        int cur=root,p=;
        while (cur && val[cur]!=x)
         p=cur,cur=t[cur][x>val[cur]];
        if (cur) cnt[cur]++;
        else {
            cur=++tot;
            if (p) t[p][x>val[p]]=cur;
            ls(cur)=rs(cur)=;
            par[cur]=p; val[cur]=x;
            size[cur]=cnt[cur]=;
        }
        splay(cur);
    }
    void find(int x){
        if (!root) return;
        int cur=root;
        while (t[cur][x>val[cur]] && val[cur]!=x)
            cur=t[cur][x>val[cur]];
        splay(cur);
    }
    int pre_id(int x) {
        find(x);
        if (val[root]<x) return root;
        int cur=ls(root);
        while (rs(cur)) cur=rs(cur);
        return cur;
    }
    int pre_val(int x){
        return val[pre_id(x)];
    }
    int suc_id(int x) {
        find(x);
        if (val[root]>x) return root;
        int cur=rs(root);
        while (ls(cur)) cur=ls(cur);
        return cur;
    }
    int suc_val(int x){
        return val[suc_id(x)];
    }
    int rank(int x){
        find(x);
        if (val[root]>=x) return size[ls(root)];
        else return size[ls(root)]+cnt[root]-;
    }
    int kth_id(int k) {
        if (k>tot||k<) return -;
        int cur=root;
        while (true) {
            if (t[cur][]&&k<=size[ls(cur)]) cur=ls(cur);
            else if (k>size[ls(cur)]+cnt[cur]) {
                k-=size[ls(cur)]+cnt[cur];
                cur=rs(cur);
            } else return cur;
        }
    }
    int kth_val(int k){
        return val[kth_id(k+)];
    }
    void erase(int x){
        int last=pre_id(x);
        int next=suc_id(x);
        splay(last);
        splay(next,last);
        int d=ls(rs(root));
        if (cnt[d]>) cnt[d]--,splay(d);
        else t[next][]=;
    }
}tr;
int main()
{
    int T; scanf("%d",&T);
    while (T--) {
        int op,x;
        scanf("%d%d",&op,&x);
        switch(op) {
            case :tr.insert(x);break;
            case :tr.erase(x);break;
            case :printf("%d\n",tr.rank(x));break;
            case :printf("%d\n",tr.kth_val(x));break;
            case :printf("%d\n",tr.pre_val(x));break;
            case :printf("%d\n",tr.suc_val(x));break;
        }
    }
    return ;
}

P3369-Splay做法