2018牛客网暑假ACM多校训练赛（第十场）F Rikka with Line Graph 最短路 Floyd

原文链接https://www.cnblogs.com/zhouzhendong/p/NowCoder-2018-Summer-Round10-F.html

题目传送门 - https://www.nowcoder.com/acm/contest/148/F

题意

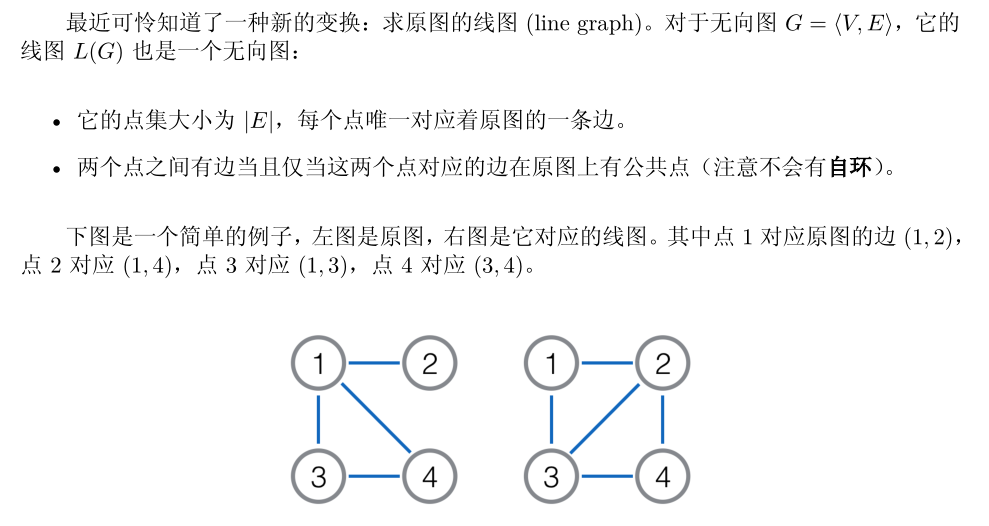
　　给定一个完全图 $G$ ，有边权。

　　定义其线图的一条边的权值为“该边连接的两个点，在原图中对应的边 的权值和”。

　　在图 $L(G)$ 上，定义 $dis(i,j)$ 为节点 $i,j$ 之间的最短路。

　　求 $\sum_{i=1}^{n}\sum_{j=i+1}^{n}dis(i,j)$ 。

　　$n\leq 500,边权 \leq 10^9,{\rm Time\ Limit\ = \ 10s}$

题解

　　线图很大，我们不大可能把它建出来，所以，我们首先考虑在 $L(G)$ 上，两个点的距离是什么。

　　对于 $L(G)$ 上的一条路径，我们把它包含的点还原到原图 $G$ 上，可以得到原图上的一些边顺次连接得到的路径。容易发现，在计算 $dis$ 时，这条路径上，两端的边的权值被算了一次，中间的被算了两次。

　　简单分析可得，两端的边的权值一定会被算一次。而中间的可以随便弄。

　　记原图中，编号为 $i$ 的边的权值为 $w_i$ 。

　　于是，计算 $dis(a,b) _{in\ L(G)} = w_a+w_b+2\times dis(x,y)_{in\ G}$

　　这个 $x,y$ 分别指 把路径搞到原图上之后，除掉两端点，剩下的两个端点的节点编号。显然我们要让这个 $dis(x,y)_{in\ G}$ 最小。考虑到 $x$ 可以选择 $a$ 的任意一个端点，$y$ 可以选择 $b$ 的任意一个端点，所以我们可以 Floyd 预处理最短路，在这 $4$ 种情况下取最小值，来方便的计算线图上任意两个点的距离。

　　考虑枚举线图上的一个点，即原图上的一条边 $(a,b)$ ，首先，两端的被算一次的边的贡献是好求的，我们考虑如何求被算两倍的那部分。考虑求出每一个点距离 $a,b$ 的最短路的最小值，后面称为“距离”，我们需要得到另一条边。对于原图上的每一个点，我们强制可以和他配对的点的距离比他大（相等的情况先搁着），这样，我们只要对于每一个点，知道有多少个点的距离比他大就好了。显然我们可以对于每一个点的距离大小排个序，就可以很方便的算出来了，而且有距离相等的情况也可以搞定了。

　　但是这样的复杂度是 $O(n^3\log n)$ 的，显然不能通过。

　　我们考虑把排序的那一只 $log$ 省掉。只需要预处理每一个节点到其他节点的距离，并从小到大排列，然后我们要得到两个点的，归并一下就好了。

　　这样，Floyd 是 $O(n^3)$ 的；枚举一条边是 $O(n^2)$ 的，得到边后的处理是 $O(n)$ 的，所以总复杂度也是 $O(n^3)$ 的。

　　最终时间复杂度 $O(n^3)$ 。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=505,mod=998244353;
int read(){
	int x=0;
	char ch=getchar();
	while (!isdigit(ch))
		ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
}
int T,n,f[N],d[N][N],dis[N];
LL g[N][N],yg[N][N];
int cmpv_id;
bool cmp(int a,int b){
	return g[cmpv_id][a]<g[cmpv_id][b];
}
void Getdis(int x,int y){
	int k=0;
	memset(f,0,sizeof f);
	int v1=1,v2=1;
	while (1){
		while (v1<=n&&f[d[x][v1]])
			v1++;
		while (v2<=n&&f[d[y][v2]])
			v2++;
		if (v1>n&&v2>n)
			break;
		if (v1>n){
			f[d[y][v2]]=1;
			dis[++k]=g[y][d[y][v2++]];
		}
		else if (v2>n){
			f[d[x][v1]]=1;
			dis[++k]=g[x][d[x][v1++]];
		}
		else if (g[x][d[x][v1]]<=g[y][d[y][v2]]){
			f[d[x][v1]]=1;
			dis[++k]=g[x][d[x][v1++]];
		}
		else {
			f[d[y][v2]]=1;
			dis[++k]=g[y][d[y][v2++]];
		}
	}
}
void solve(){
	n=read();
	int tot=0;
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			yg[i][j]=g[i][j]=read(),tot=(tot+g[i][j])%mod;
	tot=1LL*tot*((mod+1)/2)%mod;
	for (int k=1;k<=n;k++)
		for (int i=1;i<=n;i++)
			for (int j=1;j<=n;j++)
				g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
	for (int i=1;i<=n;i++){
		for (int j=1;j<=n;j++)
			d[i][j]=j;
		cmpv_id=i;
		sort(d[i]+1,d[i]+n+1,cmp);
	}
	int ans=0,e=n*(n-1)/2;
	for (int x=1;x<=n;x++)
		for (int y=x+1;y<=n;y++){
			Getdis(x,y);
//			printf("(%d,%d)\n",x,y);
//			for (int i=1;i<=n;i++)printf("%d ",dis[i]);puts("");
			ans=(1LL*(e-1)*yg[x][y]+ans)%mod;
			ans=((ans+tot-yg[x][y])%mod+mod)%mod;
			for (int i=1;i<=n;i++)
				ans=(2LL*dis[i]*(n-i)+ans)%mod;
		}
	ans=1LL*ans*((mod+1)/2)%mod;
	printf("%d\n",ans);
}
int main(){
	T=read();
	while (T--)
		solve();
	return 0;
}