HDU 1025(最长上升子序列)

题意是要在两条平行线间连点，要在线不交叉的前提下尽可能多的连线，问最多能连多少条线。

现假定题中所给的是 9 组点，分别是：1—3，2—8，3—5，4—9，5—2，6—4，7—6，8—7，9—1，如图示：

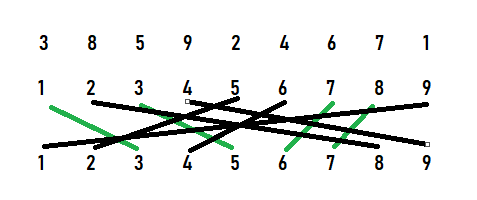 则将所给的每组 p 和 r 存在数组 a[ ] 中：a[ p ] = r；

问题就转化成了在数组 a[ ] 中求最长上升子序列的长度。显然要是直接暴力做的话，每个数字都有选和不选两种可能，那么就是 O( 2 ^ n ) 的复杂度，这是无法接受的。

除暴力外求解最长上升子序列长度的方法有三种（仅本人了解到的）：

一、直接用数组去记录选择到该数的最长上升子序列长度，每次从前往后扫一遍，若扫到的数字比所求解位置的数字小，且到该数字的最长上升子序列长度 +1大于已有的到该数字的最长上

升子序列长度，则更新到该数字的最长上升子序列长度，求出这些长度的最大值即为序列的最长上升子序列长度。

以上述 9 组点为例，要求 a[ ] = { 0，3，8，5，9，2，4， 6，7，1 } 的最长上升子序列长( 0 只是占位，与所求数据无关 )，则初始化数组 d[ ] 为 0 ：

d[ 1 ] = 1;

d[ 2 ] = 2; ( a[ 2 ] > a[ 1 ] && d[ 2 ] < d[ 1 ] + 1 )

d[ 3 ] = 2; ( a[ 3 ] > a[ 1 ] && d[ 3 ] < d[ 1 ] + 1 )

d[ 4 ] = 3; ( a[ 4 ] > a[ 3 ] && d[ 4 ] < d[ 3 ] + 1 )

......

得到数组 d[ ] 的最大值为 4，则数列的最长上升子序列的长度为 4 。

代码如下：

 #include <bits/stdc++.h>
 using namespace std;
 int n,p,r,cnt,len,a[],d[];
 int main()
 {
     cnt = ;
     while(~scanf("%d",&n))
     {
         memset(d,,sizeof(d));
         for(int i = ; i < n; ++i)
         {
             scanf("%d%d",&p,&r);
             a[p] = r;
         }
         len = d[] = ;
         for(int i = ; i <= n; ++i)
             for(int j = ; j < i; j++)
             {
                 if(a[i]>a[j] && d[i]<d[j]+)
                     d[i] = d[j]+;
                 else d[i] = ;
                 if(len < d[i]) len = d[i];
             }
         printf("Case %d:\n",cnt++);
         if(len==) printf("My king, at most 1 road can be built.\n\n");
         else printf("My king, at most %d roads can be built.\n\n",len);
     }
     return ;
 }

但是这种 O( n ^ 2 ) 复杂度的方法是会超时的。

二、多开一个数组存放当前已选中数的顺序，用二分的方法依次找到每一个待处理数字的位置再对所选序列进行调整，调整的方法就是将所处理数字按序插入所选序列中，用它替换比它大的下一个数，

若所选序列不存在比它大的数，则将它直接加在所选序列的最后，序列最终的长度就是数列的最大上升子序列长度。主要的思想就是在不损失已有最大升序长度的基础之上将大的数换小，

增大后续出现的数字比当前所选序列最大值更大的可能性。

继续以上述 9 组点为例，这一次的数组 a[ ] 仍然存放数列，数组 d[ ] 存放所选数列：

d[ ] = { 3 }, len = 1; （第一个数 3 直接加入所选序列）

d[ ] = { 3，8 }, len = 2; （第二个数 8 ，所选序列中没有比它大的数，直接加在最后）

d[ ] = { 3，5 }, len = 2; （第三个数 5 ，位于所选序列的 3 与 8 之间，以 5 替换 8 ）

d[ ] = { 3，5，9 }, len = 3; （第四个数 9 ，所选序列中没有比它大的数，直接加在最后）

d[ ] = { 2，5，9 }, len = 3; （第五个数 2 ，位于所选序列的 3 之前，以 2 替换 3 ）

d[ ] = { 2，4，9 }, len = 3; （第六个数 4 ，位于所选序列的 2 与 5 之间，以 4 替换 5 ）

d[ ] = { 2，4，6 }, len = 3; （第七个数 6 ，位于所选序列的 4 与 9 之间，以 6 替换 9 ）

d[ ] = { 2，4，6，7 }, len = 4; （第八个数 7 ，所选序列中没有比它大的数，直接加在最后）

d[ ] = {1，4，6，7 }, len = 4; （第九个数 1 ，位于所选序列的 2 之前，以 1 替换 2）

则数列的最长上升子序列长度为 4 。

代码如下：

 #include <bits/stdc++.h>
 using namespace std;
 int n,len,cnt,a[],d[];
 int getp(int x,int l,int r)
 {
     int mid;
     while(l <= r)
     {
         mid = (l+r)>>;
         if(d[mid] == x) return mid;
         if(d[mid] > x) r = mid-;
         else l = mid+;
     }
     return l;
 }
 int main()
 {
     int p,r;
     cnt = ;
     while(~scanf("%d",&n))
     {
         for(int i = ; i < n; ++i)
         {
             scanf("%d%d",&p,&r);
             a[p] = r;
         }
         d[] = a[];
         len = ;
         for(int i = ; i <= n; ++i)
         {
             if(a[i]>d[len-]) d[len++] = a[i];
             else d[getp(a[i],,len)] = a[i];
         }
         printf("Case %d:\n",cnt++);
         if(len==) printf("My king, at most 1 road can be built.\n\n");
         else printf("My king, at most %d roads can be built.\n\n",len);
     }
     return ;
 }

这个做法仅 O( nlogn ) 的复杂度，主要是在找所处理数在所选序列的位置时使用了二分的方法优化得到的。

三、树状数组优化。等今晚学会了明天再写......

致谢：　https://www.cnblogs.com/GodA/p/5180560.html

　　　　https://blog.csdn.net/George__Yu/article/details/75896330

　　　　https://blog.csdn.net/u011721440/article/details/21107113

　　　　非常感谢这些博客作者的贡献。