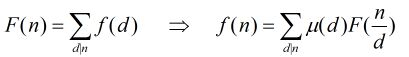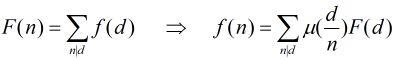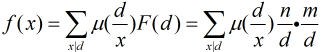HDU 1695 GCD (莫比乌斯反演模板)
GCD
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 17212 Accepted Submission(s): 6637
Problem Description
Given 5 integers: a, b, c, d, k, you're to find x in a...b, y in c...d that GCD(x, y) = k. GCD(x, y) means the greatest common divisor of x and y. Since the number of choices may be very large, you're only required to output the total number of different number pairs.
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.
Yoiu can assume that a = c = 1 in all test cases.
Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 3,000 cases.
Each case contains five integers: a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000, as described above.
Output
For each test case, print the number of choices. Use the format in the example.
Sample Input
2
1 3 1 5 1
1 11014 1 14409 9
Sample Output
Case 1: 9
Case 2: 736427
Hint
For the first sample input, all the 9 pairs of numbers are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 5), (3, 4), (3, 5).
题解:
题意是求满足1<=x<=b和1<=y<=d的gcd(x,y)=k的(x,y)有多少对,可以转化为求1<=x<=b/k和1<=y<=d/k的gcd(x,y)=1的(x,y)有多少对,可以用到莫比乌斯反演解决,证明链接https://blog.csdn.net/outer_form/article/details/50588307
这里运用到第二个式子:
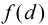
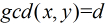
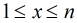
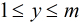
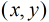
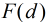
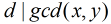
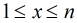
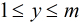
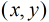
那么,一个数对x,y要满足它们的gcd是i的倍数,则x和y中都必须包含i这个因子,所以F(i)=⌊N/i⌋·⌊M/i⌋。所以反演后得到
所以得到 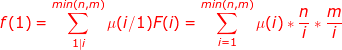
#include<iostream>
#include<string.h>
#define ll long long
using namespace std;
ll mu[100007],prime[100007];
bool mark[100007];
void getmu()
{
mu[1]=1;
ll cnt=0;
for(ll i=2;i<100007;i++){
if(!mark[i]){
prime[cnt++]=(ll)i;
mu[i]=-1;
}
for(ll j=0;j<cnt&&i*prime[j]<100007;j++){
mark[i*prime[j]]=1;
if(i%prime[j]){
mu[i*prime[j]]=-mu[i];
}else{
mu[i*prime[j]]=0;
break;
}
}
}
}
int main()
{
int T;
ll a,b,c,d,k,ans1,ans2;
getmu();
scanf("%d",&T);
for(int ca=1;ca<=T;ca++){
scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
printf("Case %d: ",ca);
if(!k){printf("0\n");continue;}
b/=k,d/=k;
if(b>d) swap(b,d);
ans1=ans2=0;
for(ll i=1;i<=b;i++)
ans1+=mu[i]*(b/i)*(d/i);
for(ll i=1;i<=b;i++)
ans2+=mu[i]*(b/i)*(b/i);
printf("%lld\n",ans1-ans2/2);
}
return 0;
}
HDU 1695 GCD (莫比乌斯反演模板)的更多相关文章
- hdu 1695 GCD 莫比乌斯反演入门
GCD 题意:输入5个数a,b,c,d,k;(a = c = 1, 0 < b,d,k <= 100000);问有多少对a <= p <= b, c <= q <= ...
- HDU 1695 GCD 莫比乌斯反演
分析:简单的莫比乌斯反演 f[i]为k=i时的答案数 然后就很简单了 #include<iostream> #include<algorithm> #include<se ...
- hdu 1695 GCD 莫比乌斯
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- [BZOJ 2820] YY的gcd(莫比乌斯反演+数论分块)
[BZOJ 2820] YY的gcd(莫比乌斯反演+数论分块) 题面 给定N, M,求\(1\leq x\leq N, 1\leq y\leq M\)且gcd(x, y)为质数的(x, y)有多少对. ...
- HDU 1695 GCD 欧拉函数+容斥定理 || 莫比乌斯反演
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- HDU 1695 GCD (莫比乌斯反演)
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- hdu 1695: GCD 【莫比乌斯反演】
题目链接 这题求[1,n],[1,m]gcd为k的对数.而且没有顺序. 设F(n)为公约数为n的组数个数 f(n)为最大公约数为n的组数个数 然后在纸上手动验一下F(n)和f(n)的关系,直接套公式就 ...
- ●HDU 1695 GCD
题链: http://acm.hdu.edu.cn/showproblem.php?pid=1695 题解: 容斥. 莫比乌斯反演,入门题. 问题化简:求满足x∈(1~n)和y∈(1~m),且gcd( ...
- hdu1695(莫比乌斯反演模板)
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=1695 题意: 对于 a, b, c, d, k . 有 x 属于 [a, b], y 属于 [c, ...
随机推荐
- flask 连接mysql及基本操作
#导入第三方连接库sql点金术 from flask_sqlalchemy import SQLAlchemy #建立对象 app = Flask(__name__) #载入配置文件 app.conf ...
- Golang记录、计算函数执行耗时、运行时间的一个简单方法
// 写超时警告日志 通用方法 func TimeoutWarning(tag, detailed string, start time.Time, timeLimit float64) { ...
- python print输出带颜色 总结
书写格式: 开头部分:\033[显示方式;前景色;背景色m + 结尾部分:\033[0m 注意:开头部分的三个参数:显示方式,前景色,背景色是可选参数,可以只写其中的某一个:另外由 ...
- (转载)经典计算机视觉论文笔记——DeepFace\DeepID\DeepID2\DeepID3\FaceNet\VGGFace汇总
1. DeepFace:Closing the Gap to Human-Level Performance in Face Verification 最早将深度学习用于人脸验证的开创性工作.Face ...
- yolo
 将目标检测过程设计为为一个回归问题(One Stage Detection),一步到位, 直接从像素到 bbox 坐标和类别概率 优点: 速度快(45fps),效果还不错(mAP 63.4) 利用 ...
- Pyperclip could not find a copy/paste mechanism for your system.
sudo apt-get install xsel sudo apt-get install xclip pip install gtk to install the gtk Python modul ...
- python字典不区分大小写
from multidict import CIMultiDict dic=CIMultiDict() dic["key"]="1234" print(dic[ ...
- C#代码处理前台html标签拼接
之前一篇文章是写,JavaScript处理特殊字符拼接时截断问题.最近在处理公司老软件兼容性升级时碰到的一个类似的问题,这次是后台拼接字符串,前台.aspx页面显示的.中间走了两次弯路,在此记录一下. ...
- 使用命令行解析php文件
使用命令行解析php文件,这样可以调用Log4PHP库中的一些demo,因为默认的输出使用命令行作为输出. 建一个bat文件: echo 以下是使用命令行解析php文件 C:\xampp\php\ph ...
- vue-cli(vue脚手架)超详细教程
都说Vue2简单上手容易,的确,看了官方文档确实觉得上手很快,除了ES6语法和webpack的配置让你感到陌生,重要的是思路的变换,以前用jq随便拿全局变量和修改dom的锤子不能用了,vu ...