Stack Pointer Tracker

在Intel 64与IA-32架构中，存在一类用于跳转到以及跳出程序段的指令：PUSH、POP、CALL、LEAVE与RET。这些指令可以在没有其余指令的干预下隐式地更新栈寄存器（ESP），维护栈内的参数，然后再执行其它相应的操作。在P3处理器之前，这类指令都会被解码成多条μops。

从PM处理器开始，引入了Stack Pointer Tracker技术。PM处理器的decoder中添加了对上述指令的处理逻辑，使得上述指令中的隐式更新ESP部分可以在decoder内完成。这种技术带来了以下便利：

节约解码带宽，因为少输出了一个更新ESP的μop，PUSH、POP、以及RET都变成了单μop指令。
节约执行带宽，因为更新ESP的运算不用在EU内执行了。
提升了out-of-order处理的并行度，因为ESP间的隐式依赖已经被消除。
降低了功耗，因为ESP的更新采用了更小型的硬件。

不过ESP除了上述指令中的隐式运算外，还能进行显式运算。ESP的隐式运算是在decoder中以in-order顺序进行的，而显式运算是在execution unit中以out-of-order顺序进行的，为了使得ESP相关指令正确执行，有必要对decoder以及EU中的ESP进行同步。同步分为两部分：

decoder执行完ESP相关运算后，把ESP更新到EU。
EU执行完ESP相关运算后，把ESP更新到decoder。

这需要EU以及decoder有对ESP的跟踪能力（Stack Pointer Tracking），不过由于指令在经过renamer的时候有用RAT记录了所有寄存器的映射，因此不单单EU，decoder也能跟踪到ESP的变化。

sync ESP from decoder to EU

decoder向EU更新ESP的实现方法是把ESP分为两部分

ESP_P = ESP_O + ESP_D

其中ESP_P是程序员眼中的ESP值（ESP实际值）；ESP_O是EU中用到的ESP，显式的ESP运算会用到该数值；ESP_D是decoder中维护的差值，隐式ESP运算会修改这个数值。以下面的例子来阐述其中机制（仅供参考）

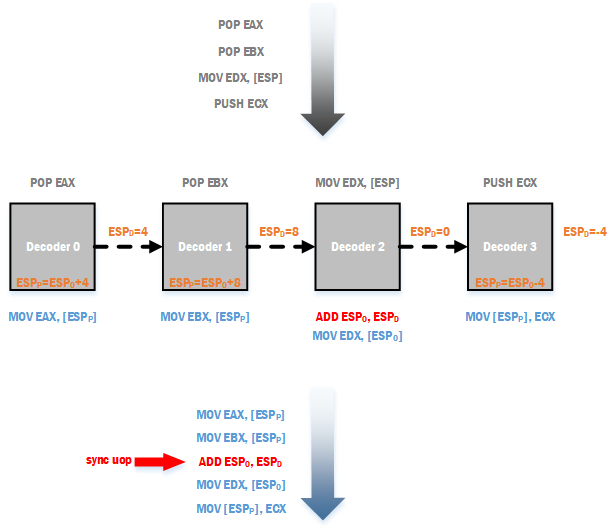
如上图所示，在解码POP/PUSH等隐式修改ESP的指令的时候，可以得到这些指令对ESP修改的差值ESP_D，然后通过这些差值，decoder内部的硬件逻辑可以直接算出ESP_P并用于这类指令的后续操作。一旦碰上显式访问ESP的指令，如果此时ESP_D不为0，则插入一条用于更新ESP_O的μop，然后把ESP_D置为0。

sync ESP from EU to decoder

由于在pipeline中decoder位于EU的前方，所以有可能会出现这种情况：decoder在计算ESP_P时，所需的ESP_O还没处理完成，此时ESP_P只能依靠推测来得到，即speculative calculation。由于可能会推测错误，因此在得到ESP_O后还需要进行判断，如果出错则应该把指令回溯，重新以正确的ESP再次执行。有兴趣的可以查看Reference中的第二三条链接作为拓展阅读。

优化建议

StackPointerTracker会在隐式修改ESP指令之后的第一条显式访问ESP的指令插入一条同步指令，因此如果对ESP的隐式修改与显式访问指令频繁交替，则会不断添加同步μop，因而会影响指令的处理效率。不过无论是隐式修改ESP还是显式访问ESP都是函数不可或缺的一部分，因此在函数体内尽量减少对ESP的隐式显式交替访问（尽量不用PUSH/POP指令），某些critical代码善用inline。

Reference：

Intel® 64 and IA-32 Architectures Optimization Reference Manual

Literature: S. Gochman, et al.: The Intel Pentium M Processor: Microarchitecture and Performance. Intel Technology Journal, vol. 7, no. 2, 2003

M. Bekerman, et al. : Early Load Address Resolution Via Register Tracking