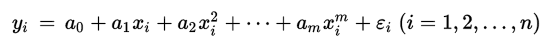[机器学习]回归--Polinomial Regression 多项式回归
首先我们需要明确一个概念,我们讨论的线性或者非线性针对的是自变量的系数,而非自变量本身,所以这样的话不管自变量如何变化,自变量的系数如果符合线性我们就说这是线性的。所以这里我们也就可以描述一下多项式线性回归。
由此公式我们可以看出,自变量只有一个,就是x,只不过x的级数(degree)不同而已。
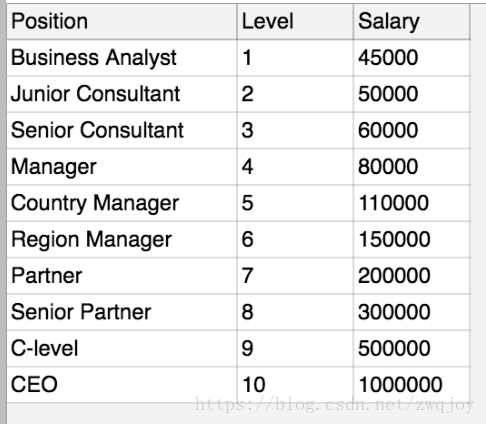
我们这次用的数据是公司内部不同的promotion level所对应的薪资
下面我们来看一下在Python中是如何实现的
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:2].values
# 这里注意:1:2其实只有第一列,与1 的区别是这表示的是一个matrix矩阵,而非单一向量。
y = dataset.iloc[:, 2].values接下来,进入正题,开始多项式线性回归:
from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree = 1) #degree 就是自变量需要的维度
X_poly = poly_reg.fit_transform(X)
lin_reg_2 = LinearRegression()
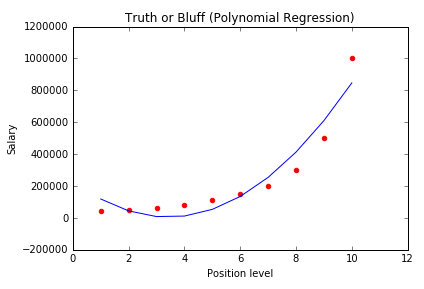
lin_reg_2.fit(X_poly, y)这个过程我们设置了一元一次的自变量:degree=1 意思是自变量只有一次,相当于简单线性回归
我们在图像中表示一下:
# 图像中显示
plt.scatter(X, y, color = 'red')
plt.plot(X, lin_reg_2.predict(poly_reg.fit_transform(X)), color = 'blue')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
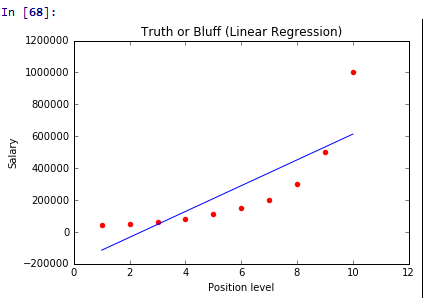
plt.show()此图像与用简单线性回归表示的图像是一样的
# 简单线性回归 图像中显示
plt.scatter(X, y, color = 'red')
plt.plot(X, lin_reg.predict(X), color = 'blue')
plt.title('Truth or Bluff (Linear Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
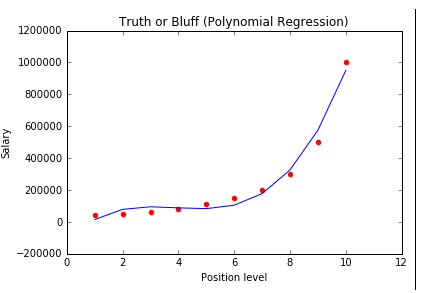
plt.show()下面我们试着改变一下维度,将degree设置成2,其他不改变,执行一下代码看看图像:
我们可以发现整个趋势符合数据的分布。
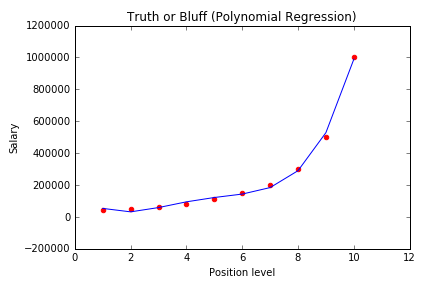
我们将degree改成3 和 4 看看结果
我们可以发现,当degree=4的时候,基本上已经符合所有点的分布了
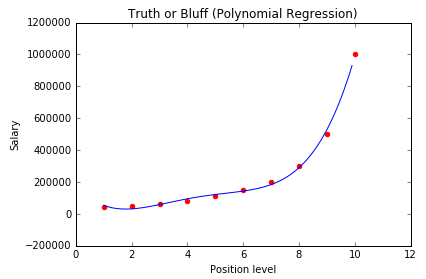
我们通过拆分横坐标将图像变得平滑一些:
X_grid = np.arange(min(X), max(X), 0.1)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(X, y, color = 'red')
plt.plot(X_grid, lin_reg_2.predict(poly_reg.fit_transform(X_grid)), color = 'blue')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
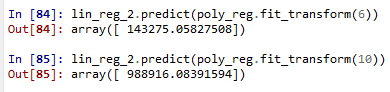
plt.show()下面我们给出一个测试值来试试结果 (6,10)
lin_reg_2.predict(poly_reg.fit_transform(6))
lin_reg_2.predict(poly_reg.fit_transform(10))与实际值还是比较接近的。
[机器学习]回归--Polinomial Regression 多项式回归的更多相关文章
- 机器学习总结之逻辑回归Logistic Regression
机器学习总结之逻辑回归Logistic Regression 逻辑回归logistic regression,虽然名字是回归,但是实际上它是处理分类问题的算法.简单的说回归问题和分类问题如下: 回归问 ...
- 机器学习入门11 - 逻辑回归 (Logistic Regression)
原文链接:https://developers.google.com/machine-learning/crash-course/logistic-regression/ 逻辑回归会生成一个介于 0 ...
- Coursera公开课笔记: 斯坦福大学机器学习第六课“逻辑回归(Logistic Regression)” 清晰讲解logistic-good!!!!!!
原文:http://52opencourse.com/125/coursera%E5%85%AC%E5%BC%80%E8%AF%BE%E7%AC%94%E8%AE%B0-%E6%96%AF%E5%9D ...
- 机器学习 (三) 逻辑回归 Logistic Regression
文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang 的个人 ...
- 机器学习(四)--------逻辑回归(Logistic Regression)
逻辑回归(Logistic Regression) 线性回归用来预测,逻辑回归用来分类. 线性回归是拟合函数,逻辑回归是预测函数 逻辑回归就是分类. 分类问题用线性方程是不行的 线性方程拟合的是连 ...
- 【机器学习实战】第8章 预测数值型数据:回归(Regression)
第8章 预测数值型数据:回归 <script type="text/javascript" src="http://cdn.mathjax.org/mathjax/ ...
- 【udacity】机器学习-回归
Evernote Export 1.什么是回归? regression 在监督学习中,包括了输入和输出的样本,在此基础上,我们能够通过新的输入来表示结果,映射到输出 输出包含了离散输出和连续输出 2. ...
- 岭回归(Ridge Regression)
一.一般线性回归遇到的问题 在处理复杂的数据的回归问题时,普通的线性回归会遇到一些问题,主要表现在: 预测精度:这里要处理好这样一对为题,即样本的数量和特征的数量 时,最小二乘回归会有较小的方差 时, ...
- 机器学习方法(五):逻辑回归Logistic Regression,Softmax Regression
欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld. 技术交流QQ群:433250724,欢迎对算法.技术.应用感兴趣的同学加入. 前面介绍过线性回归的基本知识, ...
随机推荐
- 软件测试---测试模型(V、W、H)
一.V测试模型 1.V模型示意图: 单元测试:又叫模块测试,针对软件设计中的最小单位—>程序模块 集成测试:又叫组装测试,通常在单元测试的基础上,将所有程序模块进行有序.递增测试. 系统测试:把 ...
- 解决ORA-30036:无法按8扩展段(在还原表空间‘XXXX’中)
在update一数据量很大的表时,提示“ORA-30036:无法按8扩展段” 度娘了下原因与解决办法: 1.查询了一下undo表空间的使用,发现已经超过了80% SELECT a.tablespa ...
- Fiddler-设置取消自动更新
fiddler 启动时老弹出要更新,但不想更新,可以这样设置 Tools-Optons->General 把第一个√去掉
- MySQL数据库(四)多表查询
两张假设有两张表格A和B,把表格当作一个集合,那么表格中的记录就是集合中的一个元素. 两张表格如下: TableA:TableB: 2.1 内连接(只有一种场景) inner join 或者join( ...
- CSS3新增特性及知识学习线路
- Robust Influence Maximization
一. 研究背景 在社会和经济网络中,影响最大化问题在过去十年中得到广泛的研究,由于其广泛应用于病毒式营销[1,2],突破检测[3],谣言监测[4]等.例如公司可以通过向初始用户(称为种子)发送免费 ...
- 【repost】javascript callback
在javascript中回调函数非常重要,它们几乎无处不在.像其他更加传统的编程语言都有回调函数概念,但是非常奇怪的是,完完整整谈论回调函数的在线教程比较少,倒是有一堆关于call()和apply() ...
- JObject,JArray的基本操作
引用:https://www.cnblogs.com/dacongge/p/6957074.html 1.JObject:基本的json对象 /// <summary> /// Gets ...
- Jenkins初级使用过程中的异常处理(1)
在使用Jenkins一些基本功能的时候,或者说是基本插件的时候,会遇到各种各样的报错.这里就设想模拟一下,重现一下以前遇到过的问题,记录一下.虽说是Jenkins使用过程中出现这样的问题,但实际上可以 ...
- 网络编程懒人入门(九):通俗讲解,有了IP地址,为何还要用MAC地址?
1.前言 标题虽然是为了解释有了 IP 地址,为什么还要用 MAC 地址,但是本文的重点在于理解为什么要有 IP 这样的东西.本文对读者的定位是知道 MAC 地址是什么,IP 地址是什么. (本文同步 ...