Koa 本地搭建 HTTPS 环境

openssl

首先本地需要安装 openssl，用于生成自签名证书。

$ brew install openssl

检查安装：

$ openssl version
LibreSSL 2.6.5

生成证书

执行以下命令生成证书：

openssl req -nodes -new -x509 -keyout server.key -out server.cert
Generating a 2048 bit RSA private key

执行后会提示输入一些信息，地址，组织等，可以直接回车跳过。但输入时 Common Name 时，需要确保输入 localhost。

$  openssl req -nodes -new -x509 -keyout server.key -out server.cert
Generating a 2048 bit RSA private key
............+++
..........+++
writing new private key to 'server.key'
-----
You are about to be asked to enter information that will be incorporated
into your certificate request.
What you are about to enter is what is called a Distinguished Name or a DN.
There are quite a few fields but you can leave some blank
For some fields there will be a default value,
If you enter '.', the field will be left blank.
-----
Country Name (2 letter code) []:
State or Province Name (full name) []:
Locality Name (eg, city) []:
Organization Name (eg, company) []:
Organizational Unit Name (eg, section) []:
Common Name (eg, fully qualified host name) []:localhost

执行后会得到两个文件：

• server.cert 自签名证书文件
• server.key 证书私钥

服务端代码

server.js

const http = require("http");
const https = require("https");
const fs = require("fs");
const Koa = require("koa");
const app = new Koa();

app.use(async ctx => {
  ctx.body = "hello https";
});

http.createServer(app.callback()).listen(3000);
const options = {
  key: fs.readFileSync("./server.key", "utf8"),
  cert: fs.readFileSync("./server.cert", "utf8")
};
https.createServer(options, app.callback()).listen(443);

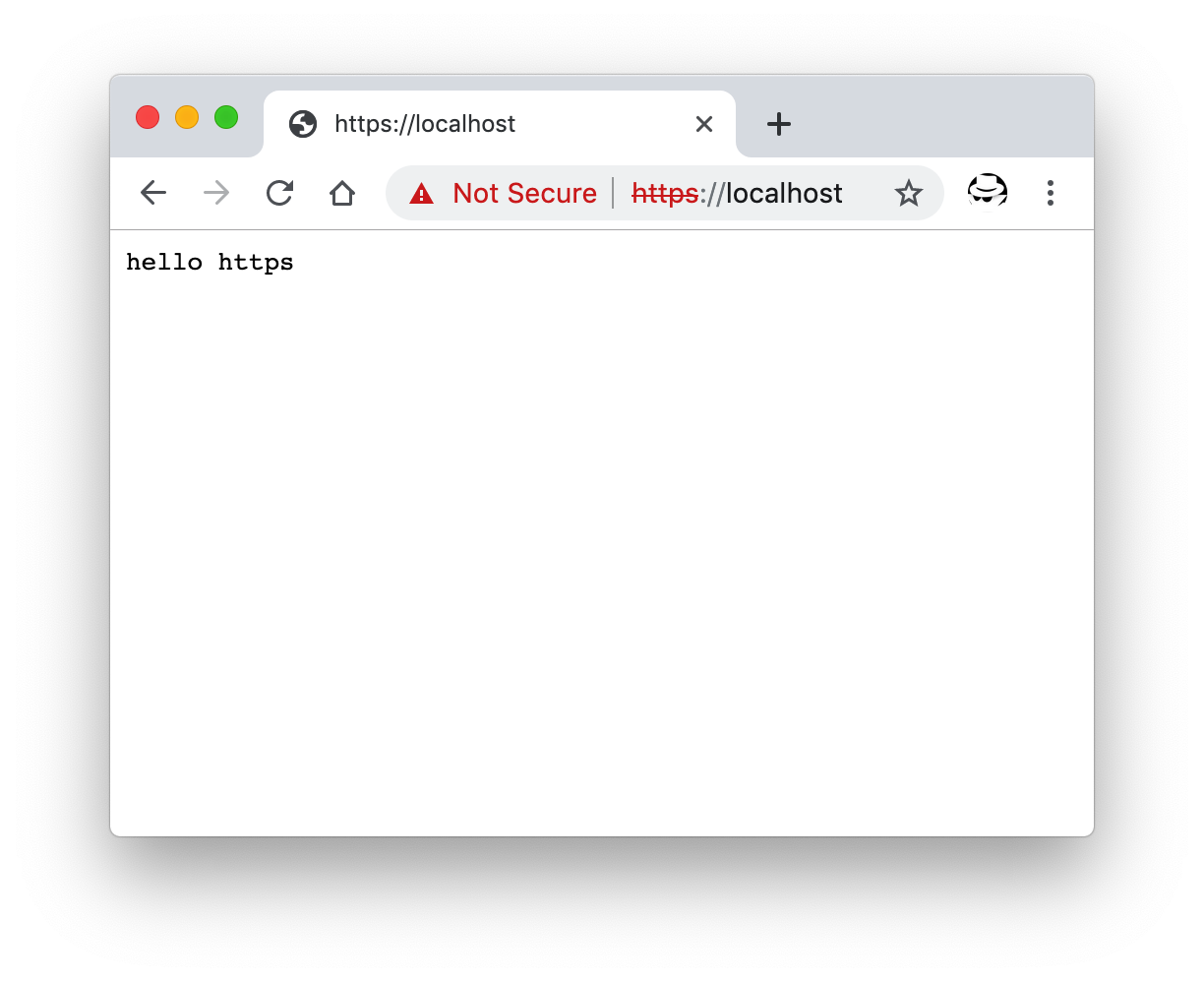
然后访问 localhost。

本地访问 https 的效果

因为是本地自签名证书的原因，并没有三方机构的认证，所以浏览器会有红色的警告。

相关资源

• An Express HTTPS server with a self-signed certificate
• Node.js Documentation - HTTPS
• How to create https server and support wss use koa2? I need it very much. #960