数据结构与算法---堆排序(Heap sort)

堆排序基本介绍

1、堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。

2、堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆, 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。

3、每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆

4、大顶堆举例说明

5、小顶堆举例说明

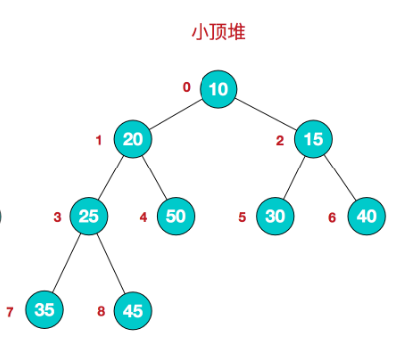
小顶堆：arr[i] <= arr[2*i+1] && arr[i] <= arr[2*i+2] // i 对应第几个节点，i从0开始编号

6、一般升序采用大顶堆，降序采用小顶堆

堆排序的基本思想是：

1. 将待排序序列构造成一个大顶堆
2. 此时，整个序列的最大值就是堆顶的根节点。
3. 将其与末尾元素进行交换，此时末尾就为最大值。
4. 然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

可以看到在构建大顶堆的过程中，元素的个数逐渐减少，最后就得到一个有序序列了.

堆排序步骤图解说明

要求：给你一个数组 {4,6,8,5,9} , 要求使用堆排序法，将数组升序排序。

步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

1) .假设给定无序序列结构如下

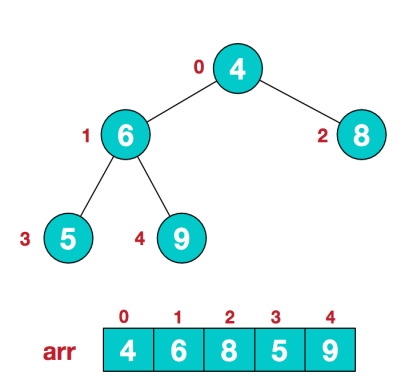
2).此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

3) .找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

4) 这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

此时，我们就将一个无序序列构造成了一个大顶堆。

步骤二 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

1) .将堆顶元素9和末尾元素4进行交换

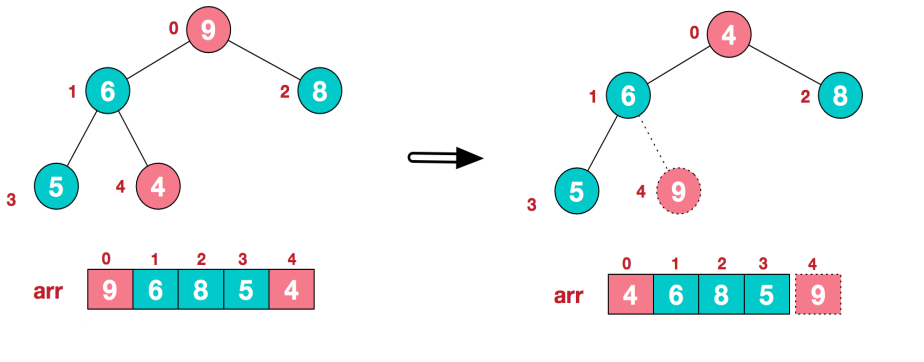
2) .重新调整结构，使其继续满足堆定义

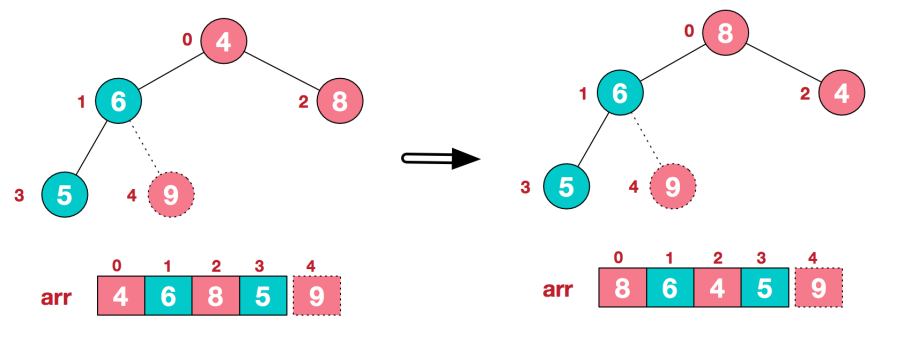
3) .再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.

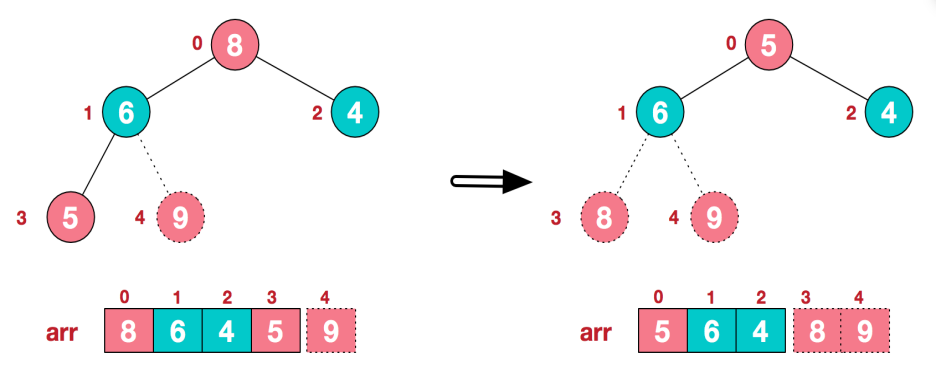
4) 后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

再简单总结下堆排序的基本思路：

1).将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

2).将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

3).重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

堆排序代码实现

要求：给你一个数组 {4,6,8,5,9} , 要求使用堆排序法，将数组升序排序.

 public class HeapSort {

     public static void main(String[] args) {
         //要求将数组进行升序排序
         //int arr[] = {4, 6, 8, 5, 9};
         // 创建要给80000个的随机的数组
         int[] arr = new int[8000000];
         for (int i = 0; i < 8000000; i++) {
             arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
         }

         System.out.println("排序前");
         Date data1 = new Date();
         SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
         String date1Str = simpleDateFormat.format(data1);
         System.out.println("排序前的时间是=" + date1Str);

         heapSort(arr);

         Date data2 = new Date();
         String date2Str = simpleDateFormat.format(data2);
         System.out.println("排序前的时间是=" + date2Str);
         //System.out.println("排序后=" + Arrays.toString(arr));
     }

     //编写一个堆排序的方法
     public static void heapSort(int arr[]) {
         int temp = 0;
         System.out.println("堆排序!!");

 //        //分步完成
 //        adjustHeap(arr, 1, arr.length);
 //        System.out.println("第一次" + Arrays.toString(arr)); // 4, 9, 8, 5, 6
 //
 //        adjustHeap(arr, 0, arr.length);
 //        System.out.println("第2次" + Arrays.toString(arr)); // 9,6,8,5,4

         //完成我们最终代码
         //将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆
         for(int i = arr.length / 2 -1; i >=0; i--) {
             adjustHeap(arr, i, arr.length);
         }

         /*
          * 2).将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
 　　            3).重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。
          */
         for(int j = arr.length-1;j >0; j--) {
             //交换
             temp = arr[j];
             arr[j] = arr[0];
             arr[0] = temp;
             adjustHeap(arr, 0, j);
         }

         //System.out.println("数组=" + Arrays.toString(arr)); 

     }

     //将一个数组(二叉树), 调整成一个大顶堆
     /**
      * 功能： 完成 将 以 i 对应的非叶子结点的树调整成大顶堆
      * 举例  int arr[] = {4, 6, 8, 5, 9}; => i = 1 => adjustHeap => 得到 {4, 9, 8, 5, 6}
      * 如果我们再次调用  adjustHeap 传入的是 i = 0 => 得到 {4, 9, 8, 5, 6} => {9,6,8,5, 4}
      * @param arr 待调整的数组
      * @param i 表示非叶子结点在数组中索引
      * @param lenght 表示对多少个元素继续调整， length 是在逐渐的减少
      */
     public  static void adjustHeap(int arr[], int i, int lenght) {

         int temp = arr[i];//先取出当前元素的值，保存在临时变量
         //开始调整
         //说明
         //1. k = i * 2 + 1 k 是 i结点的左子结点
         for(int k = i * 2 + 1; k < lenght; k = k * 2 + 1) {
             if(k+1 < lenght && arr[k] < arr[k+1]) { //说明左子结点的值小于右子结点的值
                 k++; // k 指向右子结点
             }
             if(arr[k] > temp) { //如果子结点大于父结点
                 arr[i] = arr[k]; //把较大的值赋给当前结点
                 i = k; //!!! i 指向 k,继续循环比较
             } else {
                 break;//!
             }
         }
         //当for 循环结束后，我们已经将以i 为父结点的树的最大值，放在了 最顶(局部)
         arr[i] = temp;//将temp值放到调整后的位置
     }

 }

代码

堆排序的速度非常快，在我的机器上 8百万数据 3 秒左右。O(nlogn)