【二分讲解及例题】火车站台连锁店-C++

首先我们先来从一个小游戏理解一下二分。（摘自程序员小灰的博客）

为什么说这样效率最高呢？因为每一次选择数字，无论偏大还是偏小，都可以让剩下的选择范围缩小一半。

给定范围0到1000的整数：

第一次我们选择500，发现偏大了，那么下一次的选择范围，就变成了1到499：



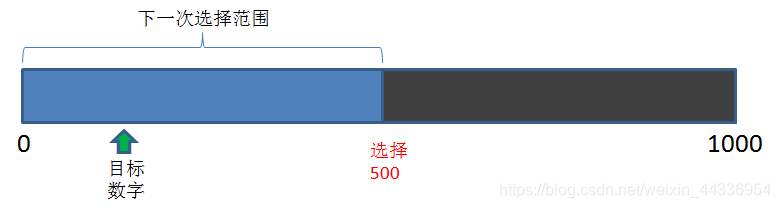
第二次我们选择250，发现还是偏大了，那么下一次的选择范围，就变成了1到249：

第三次我们选择125，发现偏小了，那么下一次的选择范围，就变成了126到249：

以此类推，最坏的情况需要猜测多少次呢？答案是 log1000 = 10次，也就是让原本的区间范围进行10次 “折半”。

所以我们很容易发现，二分查找并不会占用更多的空间，但是可以让时间复杂度从O(n)缩减到O(log(n))，这样的速度优化在程序中是非常有效的。

其次就是代码实现问题。

基本代码先贴上，先看看能不能理解：

#include<bits/stdc++.h>
using namespace std;
int a[100+1];
int main()
{
    int x,n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    cin>>x;
    int left=1,right=n;
    while(left<=right)
    {
        int mid=(left+right)/2;
        if(x==mid){cout<<"Find."<<endl<<mid;break;
        }
          if(mid>x)
          {
            right=mid+1;
          }
          else left=mid-1;
    }
    if(left>right)cout<<"Not find."<<endl;
    return 0;
}

left即本次查找区间的左边界，right同理，mid即中点，是下次折半的参照点。

如果要查找的数比中点（mid）还要小，下一次的查找区间就是从left~mid-1，

如果要查找得数比中点（mid）还要大，下一次的查找区间就是从mid+1~right.

如果左边界（left）比右边界（right）还要大，说明这个区间里没有要查找的数，即无法找到。

如果要查找的数就等于中点（mid），说明我们找到了要查找的数。

这几步如果不能理解请参照上面的漫画。

当然，递归也是可以实现的：

void binsearch(int left,int right)
{
    if(left<=right)
    {
        int mid=(left+right)/2;
        if (a[mid]==x) {cout<<"Find"<<endl;return;}
        if (x<a[mid]) binsearch(left,mid-1);
        else binsearch(mid+1,right);
    }
    else cout<<"Not Find"<<endl;
}

大致掌握了概念之后来看看例题；

火车站台连锁店
描述

蒜头君建立了一家火车站台连锁店，要在一条铁路线的所有车站里，选择一部分车站开办连锁店，销售各种口味的大蒜。

铁路线上有 n 个车站，假设这条铁路线是一条直线，其中每个站点的坐标为 x1,x2,x3,x4...xn

蒜头君一共要开办 m 个连锁店，并且不希望连锁店离得太近，以使得整体的收益最大化。他希望他的连锁店之间的最近距离尽可能大，你能帮他算出这个最大的最近距离吗？

输入
第一行输入用空格分隔的两个整数 n,m(2≤n≤10^5,2≤m≤n)，分别表示车站数量和连锁店数量。
接下来一共 n 行，每行一个整数 xi,0≤xi≤10^9，表示车站的坐标。

输出
输出一行整数，表示最大的最近距离。

输入样例 1 

6 3
1
3
5
2
7
9
输出样例 1

4
输入样例 2 

5 4
5
7
10
28
9
输出样例 2

2

先带着大家理解下题目；

在一段有n个可以开设站台的位置上，请选取其中的m个，使得每两个站台之间的最小距离取得最大值。

大概就是说，你要让这m个站台中，每两个站台之间的距离都尽可能的大。

这道题的二分思路有点复杂emm

首先我们不能直接二分因为压根找不到可以二分的东西

然后因为题目要求输出最短位置，我索性就把最短距离拿来二分！

但是我们需要一个辅助函数count来计算以L为最短距离能够开设多少家店。

函数构造很简单，直接贴上来了：

int count(int l)
{
    int last=1,ans=1;
    for(int i=1;i<=n;i++)
    {
        while(a[i]-a[last]<l)
        {
            i++;
            if(i>n)return ans;
        }
        last=i;
        ans++;
    }
    return ans;
}

怎么实现查找？

1.首先确定初始范围

因为我们要把最短距离进行二分查找，所以我们需要一个最初始的left以及right的值。可以肯定的是,这个最短距离L一定在1~最大坐标-最小坐标。

2.画图模拟查找过程!

先假设这个图长这个样子：（n=5，m=4）



第一次L的查找的区间是1~13此时mid=7,将mid传入函数count，发现可以开设2家店。

因为2<m(4)，所以下一次查找区间变成1~7。（left=1，right=7）

第二次L的查找的区间是1~7此时mid=4，将mid传入函数count，发现可以开设3家店。

因为3<m(4)，所以下一次查找区间变成1~4.（left=1，right=4）

第三次L的查找区间是1~4此时mid=2，将mid传入函数count，发现可以开设5家店。

因为5≥m(4)，所以下一次查找区间变成2~4.（left=2，right=4）

第四次L的查找区间是2~4,此时mid=3，将mid传入函数count，发现可以开设4家店。

因为4≥m(4)，所以下一次查找区间变成3~4（left=3，right=4）

接下来如果不停止，left和right和mid的值再也不会发生任何改变！

为什么？

我们二分的写法是while(left<right)

等等！发现什么不对了吗？

因为我们二分的写法是每次left和right其一等于mid，但当它们其中一个和mid相等的时候，这就成了一个死循环！

所以我们改成：

while(right-left>1)

这样就很好的避免了这个问题！

但是，走出二分之后，我们该输出谁的值？right？

这样是不完全正确的！

可能在最短距离为right的时候，我们无法开设得了m个店！因为我们while的写法，所以我们必须多一下判断：

if(count(right)>=m)cout<<right<<endl;
    else cout<<left<<endl;

所以当n=5,m=4,图如下的时候，应该输出的数字是3；

完整代码如下:

#include<bits/stdc++.h>
using namespace std;
int a[100000+1];
int n,m;
int count(int l)
{
    int last=1,ans=1;
    for(int i=1;i<=n;i++)
    {
        while(a[i]-a[last]<l)
        {
            i++;
            if(i>n)return ans;
        }
        last=i;
        ans++;
    }
    return ans;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    sort(a+1,a+1+n);
    int left=1,right=a[n]-a[1];
    while(right-left>1)
    {
        int mid=(left+right)/2;
        if(count(mid)>=m)
        {
            left=mid;
        }
        else right=mid;
    }
    if(count(right)>=m)cout<<right<<endl;
    else cout<<left<<endl;
    return 0;
}

ov.