损失函数———有关L1和L2正则项的理解

一、损失函：

模型的结构风险函数包括了   经验风险项  和  正则项，如下所示：

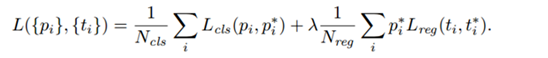
二、损失函数中的正则项

1.正则化的概念：

机器学习中都会看到损失函数之后会添加一个额外项，常用的额外项一般有2种，L1正则化和L2正则化。L1和L2可以看做是损失函数的惩罚项，所谓惩罚项是指对损失函数中某些参数做一些限制，以降低模型的复杂度。

L1正则化通过稀疏参数（特征稀疏化，降低权重参数的数量）来降低模型的复杂度；

L2正则化通过降低权重的数值大小来降低模型复杂度。

对于线性回归模型，使用L1正则化的模型叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。

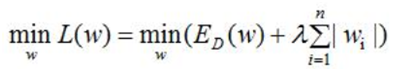
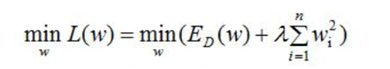
一般正则化项前面添加一个系数λ，数值大小需要用户自己指定，称权重衰减系数weight_decay，表示衰减的快慢。

2.L1正则化和L2正则化的作用：

·L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择。

·L2正则化可以减小参数大小，防止模型过拟合；一定程度上L1也可以防止过拟合

 

稀疏矩阵的概念：

·在矩阵中，若数值为0的元素数目远远超过非0元素的数目时，则该矩阵为稀疏矩阵。与之相反，若非0元素数目占大多数时，则称该矩阵为稠密矩阵。

3、正则项的直观理解

引用文档链接：

https://baijiahao.baidu.com/s?id=1621054167310242353&wfr=spider&for=pc

分别从以下角度对L1和L2正则化进行解释：

1、  优化角度分析

2、 梯度角度分析

3、 图形角度分析

4、 PRML的图形角度分析

优化角度分析：

L2正则化的优化角度分析：

即在限定区域找到使得E_D（W）最小的权重W。

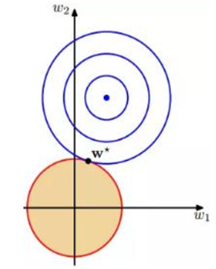
假设n=2,即只有2个参数w1和w2;作图如下：

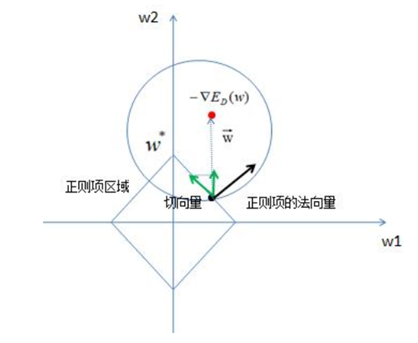
图中红色的圆即是限定区域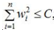，简化为2个参数就是w₁和w₂，限定区域w₁²+w₂²≤C即是以原点为圆心的圆。蓝色实线和虚线是等高线，外高内低，越靠里面的等高圆E_D（W）越小。梯度下降的方向（梯度的反方向-▽E_D（W）），即图上灰色箭头的方向，由外圆指向内圆的方向 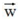表示；正则项边界上运动点P1和P2的切线用绿色箭头表示，法向量用实黑色箭头表示。切点P1上的切线在梯度下降方向有分量，仍有往负梯度方向运动的趋势；而切点P2上的法向量正好是梯度下降的方向，切线方向在梯度下降方向无分量，所以往梯度下降方向没有运动趋势，已是梯度最小的点。

结论：L2正则项使E最小时对应的参数W变小（离原点的距离更小）

L1正则化的优化角度分析：

在限定区域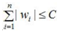，找到使E_D（w）的最小值。

同上，假设参数数量为2：w1和w2，限定区域为|w1|+|w2|≤C ,即为如下矩形限定区域，限定区域边界上的点的切向量的方向始终指向w2轴，使得w1=0,所以L1正则化容易使得参数为0，即使参数稀疏化。

梯度角度分析：

L1正则化：

L1正则化的损失函数为：

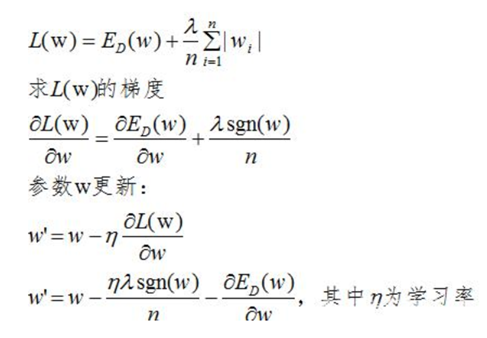
L1正则项的添加使参数w的更新增加了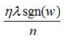，sgn(w)为阶跃函数，当w大于0，sgn(w)>0,参数w变小；当w小于0时，更新参数w变大，所以总体趋势使得参数变为0，即特征稀疏化。

L2正则化：

L2正则化的损失函数为：

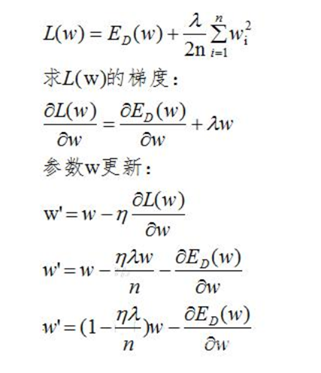
由上式可以看出，正则化的更新参数相比没有加正则项的更新参数多了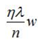，当w>0时，正则项使得参数增大变慢（减去一个数值，增大的没那么快），当w<0时，正则项使得参数减小变慢（加上一个数值，减小的没那么快），总体趋势变得很小，但不为0。

PRML的图形角度分析

L1正则化在零点附近具有很明显的棱角，L2正则化则在零附近是比较光滑的曲线。所以L1正则化更容易使参数为零，L2正则化则减小参数值，如下图。

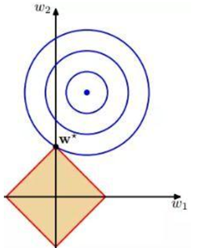
L1正则项

L2正则项

以上是根据阅读百度网友文章做的笔记（其中包括自己的理解），感谢该文档作者，引用链接：

https://baijiahao.baidu.com/s?id=1621054167310242353