locally weighted regression - CS229

欠拟合和过拟合

看下方的三张图

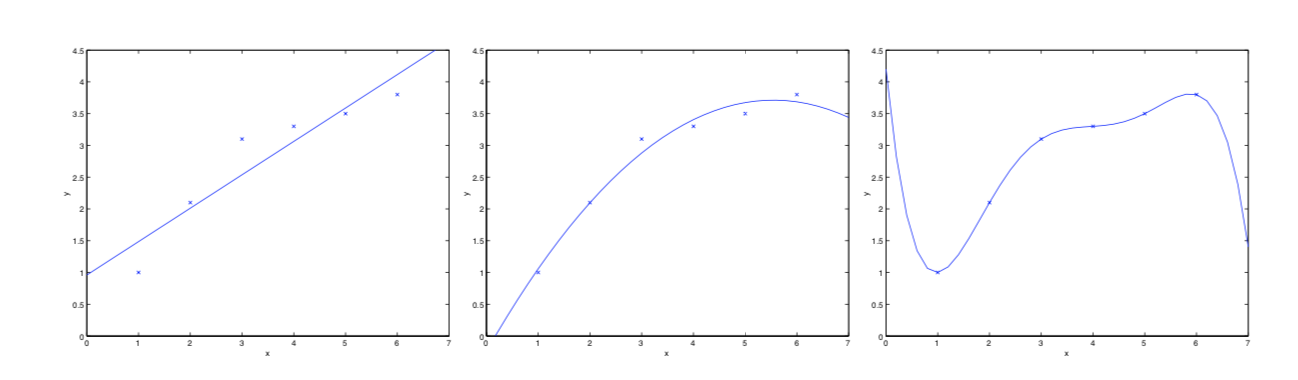
第一幅拟合为了 y=θ0+θ1xy=θ0+θ1x 的一次函数
第二幅拟合为了y=θ0+θ1x+θ2x2y=θ0+θ1x+θ2x2 的二次函数
第三幅拟合为了 y=∑5j=0θjxjy=∑j=05θjxj的五次项函数

最左边的分类器模型没有很好地捕捉到数据特征，不能够很好地拟合数据，我们称为欠拟合 
而最右边的分类器分类了所有的数据，也包括噪声数据，由于构造复杂，后期再分类的新的数据时，对于稍微不同的数据都会识别为不属于此类别，我们称为过拟合

局部加权回归

局部加权回归是一种非参数学习算法，这使得我们不必太担心对于自变量最高次项的选择

我们知道，对于普通的线性回归算法，想要预测 xx 点的yy值，我们通过：

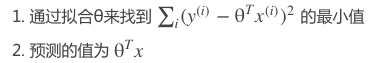
对于局部加权回归算法，我们通过下列步骤预测 y的值:

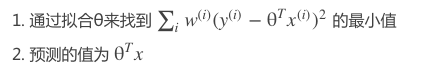
这里的 w(i)是权重，它并非一个定值，我们通过调节w(i)的值来确定不同训练数据对结果的影响力，
当w(i)很小时，它对应的y(i)−θTx(i)也很小，对结果的影响也很小；
而当它很大时，其对应的y(i)−θTx(i)也很大，对结果的影响很大。
w(i)的计算方法有很多种，其中一种公式为：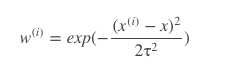

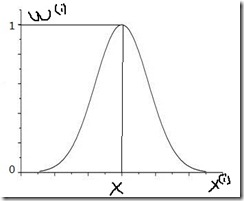
它很像高斯分布，函数图类似下图，要预测的点x对应的中间的顶点处的自变量，可以看出，离xx处越近的地方w(i)值越大,越远的地方w(i)越小，这就使得离x处近的数据对预测结果的影响更大

代码实现

 from numpy import *
 import matplotlib.pyplot as plt

 # 加载数据  返回数据和目标值
 def loadDataSet(fileName):
     numFeat = len(open(fileName).readline().split('\t')) - 1
     dataMat = []; labelMat = []
     fr = open(fileName)
     for line in fr.readlines():
         lineArr =[]
         curLine = line.strip().split('\t')
         for i in range(numFeat):
             lineArr.append(float(curLine[i]))
         dataMat.append(lineArr)
         labelMat.append(float(curLine[-1]))
     return dataMat,labelMat

 # 利用公式计算回归系数
 def standRegres(xArr,yArr):
     xMat = mat(xArr); yMat = mat(yArr).T
     xTx = xMat.T*xMat               # 公式步骤
     if linalg.det(xTx) == 0.0:
         print("行列式为0，奇异矩阵，不能做逆")
         return
     ws = xTx.I * (xMat.T*yMat)  #解线性方程组
     # ws = linalg.solve(xTx,xMat.T*yMat)  # 也可以使用函数来计算 线性方程组
     return ws

 # 局部加权线性回归 返回该条样本预测值
 def lwlr(testPoint,xArr,yArr,k=1.0):
     xMat = mat(xArr); yMat = mat(yArr).T
     m = shape(xMat)[0]
     weights = mat(eye((m)))     # 创建为单位矩阵，再mat转换数据格式     因为后面是与原数据矩阵运算，所以这里是为了后面运算且不带来其他影响
     for j in range(m):                      # 利用高斯公式创建权重W     遍历所有数据，给它们一个权重
         diffMat = testPoint - xMat[j,:]                         # 高斯核公式1
         weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))       # 高斯核公式2    矩阵*矩阵.T 转行向量为一个值    权重值以指数级衰减
     xTx = xMat.T * (weights * xMat)                             # 求回归系数公式1
     if linalg.det(xTx) == 0.0:      # 判断是否有逆矩阵
         print("行列式为0，奇异矩阵，不能做逆")
         return
     ws = xTx.I * (xMat.T * (weights * yMat))                    # 求回归系数公式2
     return testPoint * ws

 # 循环所有点求出所有的预测值
 def lwlrTest(testArr,xArr,yArr,k=1.0):  # 传入的k值决定了样本的权重，1和原来一样一条直线，0.01拟合程度不错，0.003纳入太多噪声点过拟合了
     m = shape(testArr)[0]
     yHat = zeros(m)
     for i in range(m):
         yHat[i] = lwlr(testArr[i],xArr,yArr,k)      # 返回该条样本的预测目标值
     return yHat

 xArr,yArr = loadDataSet('ex0.txt')
 # 求所有预测值
 yHat = lwlrTest(xArr,xArr,yArr,0.01)
 print(yHat)
 # 绘制数据点和拟合线（局部加权线性回归）
 xMat = mat(xArr)
 srtInd = xMat[:,1].argsort(0)   # 画拟合线 需要获得所有横坐标从小到大的下标
 xSort = xMat[srtInd][:,0,:] # 获得排序后的数据

 fig = plt.figure()
 ax = fig.add_subplot(111)
 ax.plot(xSort[:,1],yHat[srtInd],color='red')
 ax.scatter(xMat[:,1].flatten().A[0],mat(yArr).T.flatten().A[0])
 plt.show()