L1 loss, L2 loss以及Smooth L1 Loss的对比

总结对比下$L_1$ 损失函数，$L_2$ 损失函数以及$\text{Smooth} L_1$ 损失函数的优缺点。

均方误差MSE ($L_2$ Loss)

均方误差（Mean Square Error,MSE）是模型预测值$f(x)$ 与真实样本值$y$ 之间差值平方的平均值，其公式如下

\[MSE = \frac{\sum_{i=1}^n(f_{x_i} - y_i)^2}{n}
\]

其中，$y_i$和$f(x_i)$分别表示第$i$个样本的真实值及其对应的预测值，$n$为样本的个数。

忽略下标$i$ ，设$n=1$，以$f(x) - y$为横轴，MSE的值为纵轴，得到函数的图形如下：

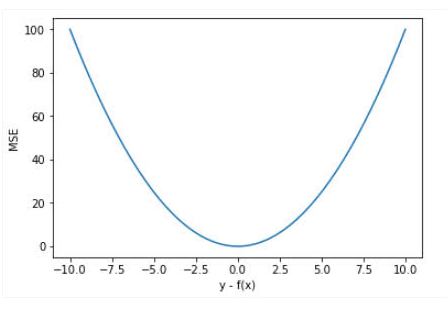
MSE的函数曲线光滑、连续，处处可导，便于使用梯度下降算法，是一种常用的损失函数。而且，随着误差的减小，梯度也在减小，这有利于收敛，即使使用固定的学习速率，也能较快的收敛到最小值。

当$y$和$f(x)$也就是真实值和预测值的差值大于1时，会放大误差；而当差值小于1时，则会缩小误差，这是平方运算决定的。MSE对于较大的误差（$>1$）给予较大的惩罚，较小的误差（$<1$）给予较小的惩罚。也就是说，对离群点比较敏感，受其影响较大。

如果样本中存在离群点，MSE会给离群点更高的权重，这就会牺牲其他正常点数据的预测效果，最终降低整体的模型性能。如下图：

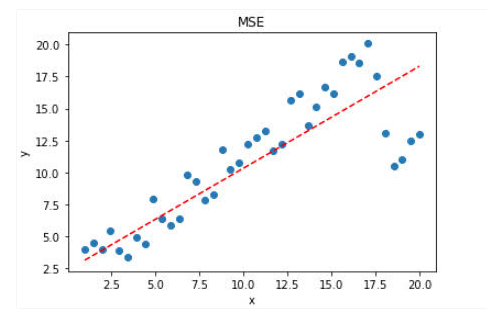
可见，使用 MSE 损失函数，受离群点的影响较大，虽然样本中只有 5 个离群点，但是拟合的直线还是比较偏向于离群点。

平均绝对误差($L_1$ Loss)

平均绝对误差（Mean Absolute Error,MAE) 是指模型预测值$f(x)$和真实值$y$之间距离的平均值，其公式如下：

\[MAE = \frac{\sum_{n=1}^n\mid f(x_i) - y_i\mid}{n}
\]

忽略下标$i$ ，设$n=1$，以$f(x) - y$为横轴，MAE的值为纵轴，得到函数的图形如下：

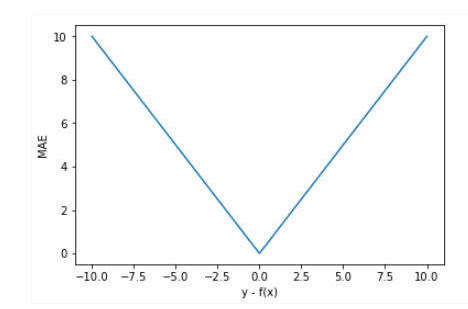
MAE曲线连续，但是在$y-f(x)=0$处不可导。而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的。这不利于函数的收敛和模型的学习。但是，无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解。

相比于MSE，MAE有个优点就是，对于离群点不那么敏感。因为MAE计算的是误差$y-f(x)$的绝对值，对于任意大小的差值，其惩罚都是固定的。

针对上面带有离群点的数据，MAE的效果要好于MSE。

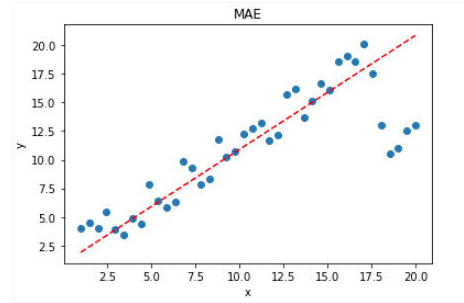
显然，使用 MAE 损失函数，受离群点的影响较小，拟合直线能够较好地表征正常数据的分布情况。

MSE和MAE的选择

从梯度的求解以及收敛上，MSE是由于MAE的。MSE处处可导，而且梯度值也是动态变化的，能够快速的收敛；而MAE在0点处不可导，且其梯度保持不变。对于很小的损失值其梯度也很大，在深度学习中，就需要使用变化的学习率，在损失值很小时降低学习率。
对离群（异常）值得处理上，MAE要明显好于MSE。

如果离群点（异常值）需要被检测出来，则可以选择MSE作为损失函数；如果离群点只是当做受损的数据处理，则可以选择MAE作为损失函数。

总之，MAE作为损失函数更稳定，并且对离群值不敏感，但是其导数不连续，求解效率低。另外，在深度学习中，收敛较慢。MSE导数求解速度高，但是其对离群值敏感，不过可以将离群值的导数设为0（导数值大于某个阈值）来避免这种情况。

在某些情况下，上述两种损失函数都不能满足需求。例如，若数据中90%的样本对应的目标值为150，剩下10%在0到30之间。那么使用MAE作为损失函数的模型可能会忽视10%的异常点，而对所有样本的预测值都为150。这是因为模型会按中位数来预测。而使用MSE的模型则会给出很多介于0到30的预测值，因为模型会向异常点偏移。

这种情况下，MSE和MAE都是不可取的，简单的办法是对目标变量进行变换，或者使用别的损失函数，例如：Huber,Log-Cosh以及分位数损失等。

Smooth $L_1$ Loss

在Faster R-CNN以及SSD中对边框的回归使用的损失函数都是Smooth $L_1$ 作为损失函数，

\[\text{Smooth}{L_1}(x) =\left \{ \begin{array}{c} 0.5x^2 & if \mid x \mid <1 \\ \mid x \mid - 0.5 & otherwise \end{array} \right.
\]

其中，$x = f(x_i) - y_i$ 为真实值和预测值的差值。

Smooth $L_1$ 能从两个方面限制梯度：

当预测框与 ground truth 差别过大时，梯度值不至于过大；
当预测框与 ground truth 差别很小时，梯度值足够小。

对比$L_1$ Loss 和 $L_2$ Loss

其中$x$为预测框与groud truth之间的差异：

\[\begin{align}
L_2(x) &= x^2 \\
L_1(x) &= x \\
smooth_{L_1}(x) &=\left \{ \begin{array}{c} 0.5x^2 & if \mid x \mid <1 \\ \mid x \mid - 0.5 & otherwise \end{array} \right.
\end{align}
\]

上面损失函数对$x$的导数为：

\[\begin{align}
\frac{\partial L_2(x)}{\partial x} &= 2x \\
\frac{\partial L_1(x)}{\partial x} &= \left \{ \begin{array}{c} 1 & \text{if } x \geq 0 \\ -1 & \text{otherwise} \end{array} \right. \\
\frac{\partial smooth_{L_1}(x)}{\partial x} &=\left \{ \begin{array}{c} x & if \mid x \mid <1 \\ \pm1 & otherwise \end{array} \right.
\end{align}
\]

上面导数可以看出：

根据公式-4，当$x$增大时，$L_2$的损失也增大。这就导致在训练初期，预测值与 groud truth 差异过于大时，损失函数对预测值的梯度十分大，训练不稳定。
根据公式-5,$L_1$对$x$的导数为常数，在训练的后期，预测值与ground truth差异很小时，$L_1$的导数的绝对值仍然为1，而 learning rate 如果不变，损失函数将在稳定值附近波动，难以继续收敛以达到更高精度。
根据公式-6，$\text{Smotth } L_1$在$x$较小时，对$x$的梯度也会变小。而当$x$较大时，对$x$的梯度的上限为1，也不会太大以至于破坏网络参数。$Smooth L_1$完美的避开了$L_1$和$L_2$作为损失函数的缺陷。

$L_1$ Loss ,$L_2$ Loss以及$Smooth L_1$ 放在一起的函数曲线对比

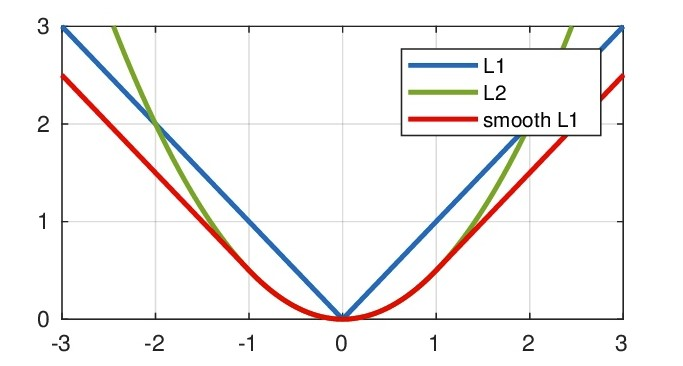
从上面可以看出，该函数实际上就是一个分段函数，在[-1,1]之间实际上就是L2损失，这样解决了L1的不光滑问题，在[-1,1]区间外，实际上就是L1损失，这样就解决了离群点梯度爆炸的问题

实现 (PyTorch)

def _smooth_l1_loss(input, target, reduction='none'):

    # type: (Tensor, Tensor) -> Tensor

    t = torch.abs(input - target)

    ret = torch.where(t < 1, 0.5 * t ** 2, t - 0.5)

    if reduction != 'none':

        ret = torch.mean(ret) if reduction == 'mean' else torch.sum(ret)

    return ret

也可以添加个参数beta 这样就可以控制，什么范围的误差使用MSE，什么范围内的误差使用MAE了。

def smooth_l1_loss(input, target, beta=1. / 9, reduction = 'none'):

    """

    very similar to the smooth_l1_loss from pytorch, but with

    the extra beta parameter

    """

    n = torch.abs(input - target)

    cond = n < beta

    ret = torch.where(cond, 0.5 * n ** 2 / beta, n - 0.5 * beta)

    if reduction != 'none':

        ret = torch.mean(ret) if reduction == 'mean' else torch.sum(ret)

    return ret

总结

对于大多数CNN网络，我们一般是使用L2-loss而不是L1-loss，因为L2-loss的收敛速度要比L1-loss要快得多。

对于边框预测回归问题，通常也可以选择平方损失函数（L2损失），但L2范数的缺点是当存在离群点（outliers)的时候，这些点会占loss的主要组成部分。比如说真实值为1，预测10次，有一次预测值为1000，其余次的预测值为1左右，显然loss值主要由1000决定。所以FastRCNN采用稍微缓和一点绝对损失函数（smooth L1损失），它是随着误差线性增长，而不是平方增长。

　　Smooth L1 和 L1 Loss 函数的区别在于，L1 Loss 在0点处导数不唯一，可能影响收敛。Smooth L1的解决办法是在 0 点附近使用平方函数使得它更加平滑。

Smooth L1的优点

相比于L1损失函数，可以收敛得更快。
相比于L2损失函数，对离群点、异常值不敏感，梯度变化相对更小，训练时不容易跑飞。