每周一练 之 数据结构与算法（Tree）

这是第六周的练习题，最近加班比较多，上周主要完成一篇 GraphQL入门教程 ，有兴趣的小伙伴可以看下哈。

下面是之前分享的链接：

• 1.每周一练 之 数据结构与算法（Stack）
• 2.每周一练 之 数据结构与算法（LinkedList）
• 3.每周一练 之 数据结构与算法（Queue）
• 4.每周一练 之 数据结构与算法（Set）
• 5.每周一练 之 数据结构与算法（Dictionary 和 HashTable）

欢迎关注我的 个人主页 && 个人博客 && 个人知识库 && 微信公众号“前端自习课”

本周练习内容：数据结构与算法 —— Tree

这些都是数据结构与算法，一部分方法是团队其他成员实现的，一部分我自己做的，有什么其他实现方法或错误，欢迎各位大佬指点，感谢。

一、什么是树？

1.树有什么特点，什么是二叉树和二叉搜索树（BST: Binary Search Tree）？

2.生活中常见的例子有哪些？

---

解析：

1. 树有什么特点，什么是二叉树和二叉搜索树：

• 树是一种非线性的数据结构，以分层方式存储数据，用来表示有层级关系的数据。

• 每棵树至多只有一个根结点，根结点会有很多子节点，每个子节点只有一个父结点。

• 父结点和子节点是相对的。

1. 生活中的例子：
   
   如：家谱、公司组织架构图。

二、请实现二叉搜索树（BST），并实现以下方法：

• insert(key)：向树中插入一个新的键；
• search(key)：树中查找一个键，如果节点存在返回true，不存在返回false；
• min()：返回树中最小的值/键；
• max()：返回树中最大的值/键；
• remove(key)：移除某个键；

提示：所谓的键对应于之前章节所学的节点（Node）

class Node {
    constructor(key){
        this.key = key
        this.left = null
        this.right = null
    }
}
class BST {
    constructor(){
        this.root = null
    }
    /**
     * 插入一个节点
     * @param {*} node 插入的位置节点
     * @param {*} newNode 插入的节点
     */
    insertNode (node, newNode){
        if(newNode.key < node.key){
            if(node.left === null && node.right === null){
                node.left = newNode
            }else if(node.left !== null && node.right === null){
                node.right = newNode
            }else{
                this.insertNode(node.left, newNode)
            }
        }else{
            if(node.left === null && node.right === null){
                node.left = newNode
            }else if(node.left !== null && node.right === null){
                node.right = newNode
            }else{
                this.insertNode(node.right, newNode)
            }
        }
    }
    /**
     * 插入操作
     * @param {*} key
     */
    insert (key){
        let newNode = new Node(key)
        if(this.root === null){
            this.root = newNode
        }else{
            this.insertNode(this.root, newNode)
        }
    }
    searchNode (node, key){
        if(node === null) return false
        if(key < node.key){
            return this.searchNode(node.left, key)
        }else if(key > node.key){
            return this.searchNode(node.right, key)
        }else{
            return true
        }
    }
    /**
     * 搜索操作
     * @param {*} key
     */
    search (key){
        return this.searchNode(this.root, key)
    }
    /**
     * 最小值的节点
     */
    min (){
        let node = this.root
        if(node === null) return null
        while(node && node.left !== null){
            node = node.left
        }
        return node.key
    }
    /**
     * 最大值的节点
     */
    max (){
        let node = this.root
        if(node === null) return null
        while(node && node.right !== null){
            node = node.right
        }
        return node.key
    }
    /**
     * 找到最小节点
     * @param {*} node
     */
    findMinNode (node){
        if(node === null) return null
        while(node && node.left !== null){
            node = node.left
        }
        return node
    }
    /**
     * 删除一个节点
     * @param {*} node
     * @param {*} key
     */
    removeNode (node, key){
        if(node === null) return null
        if(key < node.key){
            node.left = this.removeNode(node.left, key)
            return node
        }else if(key > node.key){
            node.right = this.removeNode(node.right, key)
            return node
        }else{
            // 1.叶节点
            if(node.left === null && node.right === null){
                node = null
                return node
            }
            // 2.只有一个子节点
            if(node.left === null){
                node = node.right
                return node
            }else if(node.right === null){
                node = node.left
            }
            // 3.有两个子节点
            let curNode = this.findMinNode(node.right)
            node.key = curNode.key
            node.right = this.removeNode(node.right, curNode.key)
            return node
        }
    }
    /**
     * 删除一个节点
     * @param {*} key
     */
    remove (key){
        if(this.root === null) return null
        this.root = this.removeNode(this.root, key)
    }
}

三、基于题二实现二叉搜索树扩展以下方法：

• preOrderTraverse()： 通过先序遍历方式遍历所有节点；
• inOrderTraverse()： 通过中序遍历方式遍历所有节点；
• postOrderTraverse()： 通过后序遍历方式遍历所有节点；

提示：

• 先序：先访问根节点，然后以同样方式访问左子树和右子树；（根==>左==>右）

输出 =》 11 7 5 3 6 9 8 10 15 13 12 14 20 18 25

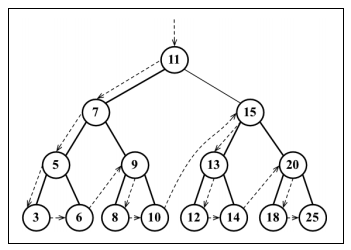
• 中序：先访问左子树，再访问根节点，最后访问右字数；以升序访问所有节点；（左==>根==>右）

输出 =》 3 5 6 7 8 9 10 11 12 13 14 15 18 20 25

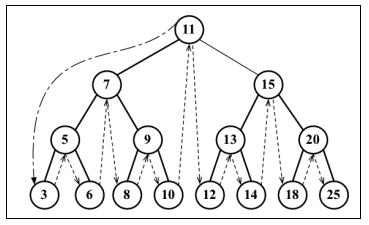
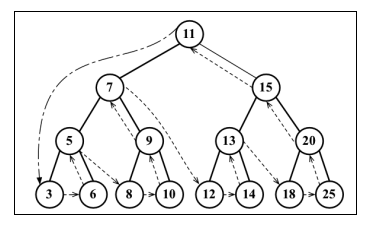
• 后序：先访问叶子节点，从左子树到右子树，再到根节点。（左==>右==>根）

输出 =》 3 6 5 8 10 9 7 12 14 13 18 25 20 15 11

---

解析：

// 1. 先序
BST.prototype.preOrderTraverseNode = function(node, callback){
    if(node !== null){
        callback(node.key)
        this.preOrderTraverseNode(node.left, callback)
        this.preOrderTraverseNode(node.right, callback)
    }
}
BST.prototype.preOrderTraverse = function(callback){
    this.preOrderTraverseNode(this.root, callback)
}

// 2. 中序
BST.prototype.inOrderTraverseNode = function(node, callback){
    if(node !== null){
        this.inOrderTraverseNode(node.left, callback)
        callback(node.key)
        this.inOrderTraverseNode(node.right, callback)
    }
}
BST.prototype.inOrderTraverse = function(callback){
    this.inOrderTraverseNode(this.root, callback)
}

// 3. 后序
BST.prototype.postOrderTraverseNode = function(node, callback){
    if(node !== null){
        this.postOrderTraverseNode(node.left, callback)
        this.postOrderTraverseNode(node.right, callback)
        callback(node.key)
    }
}
BST.prototype.postOrderTraverse = function(callback){
    this.postOrderTraverseNode(this.root, callback)
}

四、请实现从上往下打印二叉树

给定的二叉树为：[3, 9 , 20, null, null, 15, 7]

    3
   / \
  9  20
     / \
    15  7

请实现一个 printLevelOrder 方法，输出以下结果：

[
  [3],
  [9, 20],
  [15, 7]
]

---

来源：102.二叉树的层次遍历

解析：

• 方法一：

BST.prototype.printLevelOrder = function (root, arr = [], i = 0){
    if (root && (root.key || root.key === 0)) {
      !arr[i] && (arr[i] = [])
      arr[i].push(root.key)
      i++
      root.left && this.printLevelOrder(root.left, arr, i)
      root.right && this.printLevelOrder(root.right, arr, i)
    }
    return arr
}

• 方法二：

BST.prototype.printLevelOrder = function (){
    if(this.root === null) return []
    let result = [], queue = [this.root]
    while(true){
        let len = queue.length, arr = []
        while(len > 0){
            console.log(queue)
            let node = queue.shift()
            len -= 1
            arr.push(node.key)
            if(node.left !== null) queue.push(node.left)
            if(node.right !== null) queue.push(node.right)
        }
        if(arr.length === 0) return result
        result.push([...arr])
    }
}

五、给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入:
    2
   / \
  1   3
输出: true

示例 2：

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ，但是其右子节点值为 4 。

代码实现：

/**
 * 二叉树节点定义
 */
function TreeNode(val) {
  this.val = val;
  this.left = this.right = null;
}

/**
- @param {TreeNode} root
- @return {boolean}
*/
function isValidBST(root) {};

---

来源：99.验证二叉搜索树

解析：

function isValidBST(root) {
    let arr = []
    function inOrderTraverse(node){
        if(node === null) return;
        node.left && inOrderTraverse(node.left);
        arr.push(node.val);
        node.right && inOrderTraverse(node.right);
    }
    inOrderTraverse(root)
    for(let i = 0; i < arr.length - 1; i++){
        if(arr[i] >= arr[i+1]) return false
    }
    return true
};