线段树+lazy标记 2019年8月10日计蒜客联盟周赛 C.小A的题

题目链接：https://nanti.jisuanke.com/t/40852

题意：给定一个01串s，进行m次操作，|s|<=1e6，m<=5e5

操作有两种

l r 0，区间[l,r]升序排序

l r 1，区间[l,r]降序排序

输出m次操作后的串s

官方解析：

维护区间1的个数，区间0的个数=区间长度-区间1的个数，完成区间赋值操作并更新即可。

个人思路：

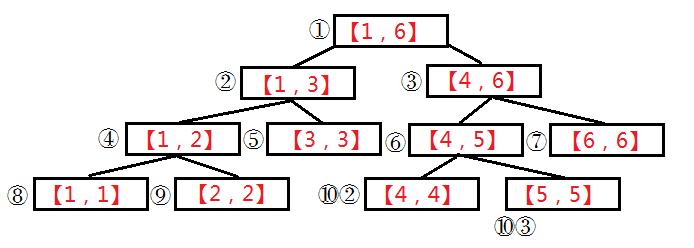
线段树的操作都是log(n)，如果带了lazy标记，就可以小于log(n)，不必查询到每个点。例如将[1,3]都置为1，只用将t[2]=3即可。

另外tag是标记升序降序的lazy标记，在update和getsum中会进行标记下放。

时间复杂度小于O（m*log(|S|)）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxl=1e6+;
const int manx=5e5+;
char s[maxl];
int t[maxl*],tag[maxl*];
inline int read()
{
    int f=,x=;char s=getchar();
    while(s<''||s>''){if(s=='-')f=-;s=getchar();}
    while(s>=''&&s<=''){x=(x<<)+(x<<)+s-'';s=getchar();}
    return x*f;
}

void build(int x,int l,int r)//t[x]记录1的个数
{
    tag[x]=-;
    if(l==r)
    {
        t[x]=s[l]-'';
        return;
    }
    int mid=(l+r)/;
    build(x*,l,mid);
    build(x*+,mid+,r);
    t[x]=t[x*]+t[x*+]; //x<<1|1
}
int getsum(int x,int l,int r,int L,int R)  //L R是要求的sum区间
{
    if(l==L&&r==R)return t[x];
    int mid=(l+r)/;
    if(tag[x]!=-)
    {
        tag[x*]=tag[x*+]=tag[x];
        t[x*]=tag[x]?(mid-l+):;
        t[x*+]=tag[x]?(r-mid):;
        tag[x]=-;
    }
    if(R<=mid)return getsum(x*,l,mid,L,R);
    else if(L>mid)return getsum(x*+,mid+,r,L,R);
    else return getsum(x*,l,mid,L,mid)+getsum(x*+,mid+,r,mid+,R);
}
void update(int x,int l,int r,int L,int R,int v)
{
    if(l==L&&r==R)
    {
        tag[x]=v;
        t[x]=v?(r-l+):;
        return;
    }
    int mid=(l+r)/;
    if(tag[x]!=-)
    {
        tag[x*]=tag[x*+]=tag[x];
        t[x*]=tag[x]?(mid-l+):;
        t[x*+]=tag[x]?(r-mid):;
        tag[x]=-;
    }
    if(R<=mid) update(x*,l,mid,L,R,v);
    else if(L>mid) update(x*+,mid+,r,L,R,v);
    else
    {
        update(x*,l,mid,L,mid,v);
        update(x*+,mid+,r,mid+,R,v);
    }
    t[x]=t[x*]+t[x*+];
}
void dfs(int x,int l,int r)
{
    if(l==r)
    {
        printf("%d",t[x]);
        return;
    }
    int mid=(l+r)/;
    if(tag[x]!=-)
    {
        tag[x*]=tag[x*+]=tag[x];
        t[x*]=tag[x]?(mid-l+):;
        t[x*+]=tag[x]?(r-mid):;
        tag[x]=-;
    }
    dfs(x*,l,mid);
    dfs(x*+,mid+,r);
}
int main()
{
    scanf("%s",s+);
    int n=strlen(s+);
    build(,,n);
    int m=read();
    int u,v,w;
    while(m--)
    {
        u=read();v=read();w=read();  //[u,v]，w=0升序，w=1降序
        int sum=getsum(,,n,u,v);  //算出有几个1
        if(sum==||sum==(v-u+))continue;
        if(w==)update(,,n,u,v-sum,),update(,,n,v-sum+,v,);
        else update(,,n,u,u+sum-,),update(,,n,u+sum,v,);
    }
    dfs(,,n);
    return ;
} 

另：移位符号计算比*号快，线段树要开四倍空间