利用Python学习线性代数 -- 1.1 线性方程组

利用Python学习线性代数系列，第一节

本节实现的主要功能函数，在源码文件linear_system中，后续章节将作为基本功能调用。

线性方程

线性方程组由一个或多个线性方程组成，如

\[\begin{array}\\
x_1 - 2 x_2 &= -1\\
-x_1 + 3 x_2 &= 3
\end{array}
\]

求包含两个变量两个线性方程的方程组的解，等价于求两条直线的交点。

这里可以画出书图1-1和1-2的线性方程组的图形。

通过改变线性方程的参数，观察图形，体会两个方程对应直线平行、相交、重合三种可能。

那么，怎么画二元线性方程的直线呢？

方法是这样的：

假如方程是 \(a x_1 + b x_2 = c\) 的形式，可以写成 \(x_2 = (c - a x_1) / b\)。

在以 \(x_1\) 和\(x_2\)为两个轴的直角坐标系中，\(x_1\)取一组值，如 \((-3, -2.9, -2.8, \dots, 2.9, 3.0)\)，

计算相应的 \(x_2\)，然后把所有点 \((x_1, x_2)\) 连起来成为一条线。

当 \(b\) 为 \(0\) 时， 则在\(x_1 = c / a\)处画一条垂直线。

  1. # 引入Numpy和 Matplotlib库
  2. import numpy as np
  3. from matplotlib import pyplot as plt

Matplotlib 是Python中使用较多的可视化库，这里只用到了它的一些基本功能。

  1. def draw_line(a, b, c, start=-4,
  2.               stop=5, step=0.01):
  3.     """根据线性方程参数绘制一条直线"""
  4.     # 如果b为0，则画一条垂线
  5.     if np.isclose(b, 0):
  6.         plt.vlines(start, stop, c / a)
  7.     else: # 否则画 y = (c - a*x) / b
  8.         xs = np.arange(start, stop, step)
  9.         plt.plot(xs, (c - a*xs)/b)
  1. # 1.1 图1-1
  2. draw_line(1, -2, -1)
  3. draw_line(-1, 3, 3)

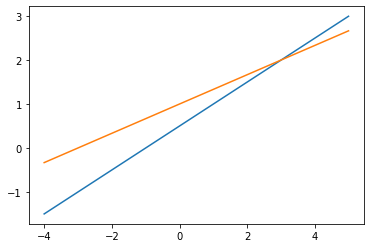
  1. def draw_lines(augmented, start=-4,
  2.               stop=5, step=0.01):
  3.     """给定增广矩阵，画两条线."""
  4.     plt.figure()
  5.     for equation in augmented:
  6.         draw_line(*equation, start, stop, step)
  7.     plt.show()
  1. # Fig. 1-1
  2. # 增广矩阵用二维数组表示
  3. # [[1, -2, -1], [-1, 3, 3]]
  4. # 这些数字对应图1-1对应方程的各项系数
  5. draw_lines([[1, -2, -1], [-1, 3, 3]])

  1. # Fig. 1-2
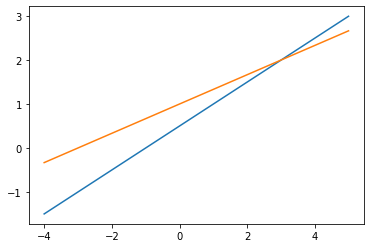
  2. draw_lines([[1, -2, -2], [-1, 2, 3]])
  3. # Fig. 1-3
  4. draw_lines([[1, -2, -1], [-1, 2, 1]])



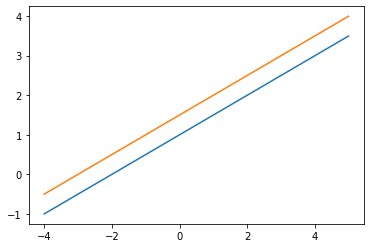
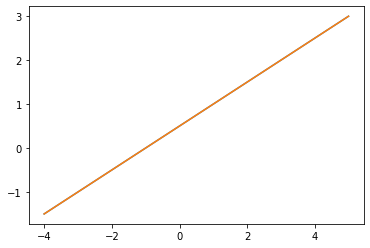
  • 建议：改变这些系数，观察直线，体会两条直线相交、平行和重合的情况

例如

  1. draw_lines([[1, -2, -2], [-1, 2, 9]])

如果对Numpy比较熟悉，则可以采用更简洁的方式实现上述绘图功能。

在计算多条直线方程时，可以利用向量编程的方式，用更少的代码实现。

  1. def draw_lines(augmented, start=-4,
  2.                stop=5, step=0.01):
  3.     """Draw lines represented by augmented matrix on 2-d plane."""
  4.     am = np.asarray(augmented)
  5.     xs = np.arange(start, stop, step).reshape([1, -1])
  6.     # 同时计算两条直线的y值
  7.     ys = (am[:, [-1]] - am[:, [1]]*xs) / am[:, [0]]
  8.     for y in ys:
  9.         plt.plot(xs[0], y)
  10.     plt.show()

矩阵记号

矩阵是一个数表，在程序中通常用二维数组表示，例如

  1. # 嵌套列表表示矩阵
  2. matrix = [[1, -2, 1, 0],
  3.           [0, 2, -8, 8],
  4.           [5, 0, -5, 10]]
  5. matrix
  1. [[1, -2, 1, 0], [0, 2, -8, 8], [5, 0, -5, 10]]

实际工程和研究实践中，往往会采用一些专门的数值计算库，简化和加速计算。

Numpy库是Python中数值计算的常用库。

在Numpy中，多维数组类型称为ndarray，可以理解为n dimensional array。

例如

  1. # Numpy ndarray 表示矩阵
  2. matrix = np.array([[1, -2, 1, 0],
  3.                     [0, 2, -8, 8],
  4.                     [5, 0, -5, 10]])
  5. matrix
  1. array([[ 1, -2,  1,  0],
  2.        [ 0,  2, -8,  8],
  3.        [ 5,  0, -5, 10]])

解线性方程组

本节解线性方程组的方法是 高斯消元法，利用了三种基本行变换。

  1. 把某个方程换成它与另一个方程的倍数的和；
  2. 交换两个方程的位置；
  3. 某个方程的所有项乘以一个非零项。

假设线性方程的增广矩阵是\(A\)，其第\(i\)行\(j\)列的元素是\(a_{ij}\)。

消元法的基本步骤是：

  • 增广矩阵中有 \(n\) 行，该方法的每一步处理一行。

    1. 在第\(i\)步，该方法处理第\(i\)行

      • 若\(a_{ii}\)为0，则在剩余行 \(\{j| j \in (i, n]\}\)中选择绝对值最大的行\(a_{ij}\)

        • 若\(a_{ij}\)为0，返回第1步。
        • 否则利用变换2，交换\(A\)的第\(i\)和\(j\)行。
    2. 利用行变换3，第\(i\)行所有元素除以\(a_{ii}\)，使第 \(i\) 个方程的第 \(i\)个 系数为1
    3. 利用行变换1，\(i\)之后的行减去第\(i\)行的倍数，使这些行的第 \(i\) 列为0

为了理解这些步骤的实现，这里先按书中的例1一步步计算和展示，然后再总结成完整的函数。

例1的增广矩阵是

\[\left[
\begin{array}
&1 & -2 & 1 & 0\\
0 & 2 & -8 & 8\\
5 & 0 & -5 & 10
\end{array}
\right]
\]

  1. # 增广矩阵
  2. A = np.array([[1, -2, 1, 0],
  3.               [0, 2, -8, 8],
  4.               [5, 0, -5, 10]])
  5. # 行号从0开始，处理第0行
  6. i = 0
  7. # 利用变换3，将第i行的 a_ii 转成1。这里a_00已经是1，所不用动
  8. # 然后利用变换1，把第1行第0列，第2行第0列都减成0。
  9. # 这里仅需考虑i列之后的元素，因为i列之前的元素已经是0
  10. #   即第1行减去第0行的0倍
  11. #   而第2行减去第0行的5倍
  12. A[i+1:, i:] = A[i+1:, i:] - A[i+1:, [i]] * A[i, i:]
  13. A
  1. array([[  1,  -2,   1,   0],
  2.        [  0,   2,  -8,   8],
  3.        [  0,  10, -10,  10]])
  1. i = 1
  2. # 利用变换3，将第i行的 a_ii 转成1。
  3. A[i] = A[i] / A[i, i]
  4. A
  1. array([[  1,  -2,   1,   0],
  2.        [  0,   1,  -4,   4],
  3.        [  0,  10, -10,  10]])
  1. # 然后利用变换1，把第2行第i列减成0。
  2. A[i+1:, i:] = A[i+1:, i:] - A[i+1:, [i]] * A[i, i:]
  3. A
  1. array([[  1,  -2,   1,   0],
  2.        [  0,   1,  -4,   4],
  3.        [  0,   0,  30, -30]])
  1. i = 2
  2. # 利用变换3，将第i行的 a_ii 转成1。
  3. A[i] = A[i] / A[i, i]
  4. A
  1. array([[ 1, -2,  1,  0],
  2.        [ 0,  1, -4,  4],
  3.        [ 0,  0,  1, -1]])

消元法的前向过程就结束了，我们可以总结成一个函数

  1. def eliminate_forward(augmented):
  2.     """
  3.     消元法的前向过程.
  5.     返回行阶梯形，以及先导元素的坐标（主元位置）
  6.     """
  7.     A = np.asarray(augmented, dtype=np.float64)
  8.     # row number of the last row
  9.     pivots = []
  10.     i, j = 0, 0
  11.     while i < A.shape[0] and j < A.shape[1]:
  12.         A[i] = A[i] / A[i, j]
  13.         if (i + 1) < A.shape[0]: # 除最后一行外
  14.             A[i+1:, j:] = A[i+1:, j:] - A[i+1:, [j]] * A[i, j:]
  15.         pivots.append((i, j))
  16.         i += 1
  17.         j += 1
  18.     return A, pivots

这里有两个细节值得注意

  1. 先导元素 \(a_{ij}\)，不一定是在主对角线位置，即 \(i\) 不一定等于\(j\).
  2. 最后一行只需要用变换3把先导元素转为1，没有剩余行需要转换
  1. # 测试一个增广矩阵，例1
  2. A = np.array([[1, -2, 1, 0],
  3.               [0, 2, -8, 8],
  4.               [5, 0, -5, 10]])
  5. A, pivots = eliminate_forward(A)
  6. print(A)
  7. print(pivots)
  1. [[ 1. -2.  1.  0.]
  2.  [ 0.  1. -4.  4.]
  3.  [ 0.  0.  1. -1.]]
  4. [(0, 0), (1, 1), (2, 2)]

消元法的后向过程则更简单一些，对于每一个主元(这里就是前面的\(a_{ii}\))，将其所在的列都用变换1，使其它行对应的列为0.

  1. for i, j in reversed(pivots):
  2.     A[:i, j:] = A[:i, j:] - A[[i], j:] * A[:i, [j]]
  3. A
  1. array([[ 1.,  0.,  0.,  1.],
  2.        [ 0.,  1.,  0.,  0.],
  3.        [ 0.,  0.,  1., -1.]])
  1. def eliminate_backward(simplified, pivots):
  2.     """消元法的后向过程."""
  3.     A = np.asarray(simplified)
  4.     for i, j in reversed(pivots):
  5.         A[:i, j:] = A[:i, j:] - A[[i], j:] * A[:i, [j]]
  6.     return A

至此，结合 eliminate_forward 和eliminate_backward函数，可以解形如例1的线性方程。

然而，存在如例3的线性方程，在eliminate_forward算法进行的某一步，主元为0，需要利用变换2交换两行。

交换行时，可以选择剩余行中，选择当前主元列不为0的任意行，与当前行交换。

这里每次都采用剩余行中，当前主元列绝对值最大的行。

补上行交换的前向过程函数如下

  1. def eliminate_forward(augmented):
  2.     """消元法的前向过程"""
  3.     A = np.asarray(augmented, dtype=np.float64)
  4.     # row number of the last row
  5.     pivots = []
  6.     i, j = 0, 0
  7.     while i < A.shape[0] and j < A.shape[1]:
  8.         # if pivot is zero, exchange rows
  9.         if np.isclose(A[i, j], 0):
  10.             if (i + 1) < A.shape[0]:
  11.                 max_k = i + 1 + np.argmax(np.abs(A[i+1:, i]))
  12.             if (i + 1) >= A.shape[0] or np.isclose(A[max_k, i], 0):
  13.                 j += 1
  14.                 continue
  15.             A[[i, max_k]] = A[[max_k, i]]
  16.         A[i] = A[i] / A[i, j]
  17.         if (i + 1) < A.shape[0]:
  18.             A[i+1:, j:] = A[i+1:, j:] - A[i+1:, [j]] * A[i, j:]
  19.         pivots.append((i, j))
  20.         i += 1
  21.         j += 1
  22.     return A, pivots

行交换时，有一种特殊情况，即剩余所有行的主元列都没有非零元素。

这种情况下，在当前列的右侧寻找不为零的列，作为新的主元列。

  1. # 用例3测试eliminate_forward
  2. aug = [[0, 1, -4, 8],
  3.        [2, -3, 2, 1],
  4.        [4, -8, 12, 1]]
  5. echelon, pivots = eliminate_forward(aug)
  6. print(echelon)
  7. print(pivots)
  1. [[ 1.   -2.    3.    0.25]
  2.  [ 0.    1.   -4.    0.5 ]
  3.  [ 0.    0.    0.    1.  ]]
  4. [(0, 0), (1, 1), (2, 3)]

例3化简的结果与书上略有不同，由行交换策略不同引起，也说明同一个矩阵可能由多个阶梯形。

结合上述的前向和后向过程，即可以给出一个完整的消元法实现

  1. def eliminate(augmented):
  2.     """
  3.     利用消元法前向和后向步骤，化简线性方程组.
  5.     如果是矛盾方程组，则仅输出前向化简结果，并打印提示
  6.     否则输出简化后的方程组，并输出最后一列
  7.     """
  8.     print(np.asarray(augmented))
  9.     A, pivots = eliminate_forward(augmented)
  10.     print(" The echelon form is\n", A)
  11.     print(" The pivots are: ", pivots)
  12.     pivot_cols = {p[1] for p in pivots}
  13.     simplified = eliminate_backward(A, pivots)
  14.     if (A.shape[1]-1) in pivot_cols:
  15.         print(" There is controdictory.\n", simplified)
  16.     elif len(pivots) == (A.shape[1] -1):
  17.         print(" Solution: ", simplified[:, -1])
  18.         is_correct = solution_check(np.asarray(augmented),
  19.                             simplified[:, -1])
  20.         print(" Is the solution correct? ", is_correct)
  21.     else:
  22.         print(" There are free variables.\n", simplified)
  23.     print("-"*30)
  1. eliminate(aug)
  1. [[ 0  1 -4  8]
  2.  [ 2 -3  2  1]
  3.  [ 4 -8 12  1]]
  4.  The echelon form is
  5.  [[ 1.   -2.    3.    0.25]
  6.  [ 0.    1.   -4.    0.5 ]
  7.  [ 0.    0.    0.    1.  ]]
  8.  The pivots are:  [(0, 0), (1, 1), (2, 3)]
  9.  There is controdictory.
  10.  [[ 1.  0. -5.  0.]
  11.  [ 0.  1. -4.  0.]
  12.  [ 0.  0.  0.  1.]]
  13. ------------------------------

利用 Sympy 验证消元法实现的正确性

Python的符号计算库Sympy，有化简矩阵为行最简型的方法，可以用来检验本节实现的代码是否正确。

  1. # 导入 sympy的 Matrix模块
  2. from sympy import Matrix
  1. Matrix(aug).rref(simplify=True)
  2. # 返回的是行最简型和主元列的位置
  1. (Matrix([
  2.  [1, 0, -5, 0],
  3.  [0, 1, -4, 0],
  4.  [0, 0,  0, 1]]), (0, 1, 3))
  1. echelon, pivots = eliminate_forward(aug)
  2. simplified = eliminate_backward(echelon, pivots)
  3. print(simplified, pivots)
  4. # 输出与上述rref一致
  1. [[ 1.  0. -5.  0.]
  2.  [ 0.  1. -4.  0.]
  3.  [ 0.  0.  0.  1.]] [(0, 0), (1, 1), (2, 3)]

综合前向和后向步骤，并结果的正确性

综合前向和后向消元，就可以得到完整的消元法过程。

消元结束，如果没有矛盾（最后一列不是主元列），基本变量数与未知数个数一致，则有唯一解，可以验证解是否正确。

验证的方法是将解与系数矩阵相乘，检查与原方程的b列一致。

  1. def solution_check(augmented, solution):
  2.     # 系数矩阵与解相乘
  3.     b = augmented[:, :-1] @ solution.reshape([-1, 1])
  4.     b = b.reshape([-1])
  5.     # 检查乘积向量与b列一致
  6.     return all(np.isclose(b - augmented[:, -1], np.zeros(len(b))))
  1. def eliminate(augmented):
  2.     from sympy import Matrix
  3.     print(np.asarray(augmented))
  4.     A, pivots = eliminate_forward(augmented)
  5.     print(" The echelon form is\n", A)
  6.     print(" The pivots are: ", pivots)
  7.     pivot_cols = {p[1] for p in pivots}
  8.     simplified = eliminate_backward(A, pivots)
  9.     if (A.shape[1]-1) in pivot_cols: # 最后一列是主元列
  10.         print(" There is controdictory.\n", simplified)
  11.     elif len(pivots) == (A.shape[1] -1): # 唯一解
  12.         is_correct = solution_check(np.asarray(augmented),
  13.                             simplified[:, -1])
  14.         print(" Is the solution correct? ", is_correct)
  15.         print(" Solution: \n", simplified)
  16.     else: # 有自由变量
  17.         print(" There are free variables.\n", simplified)
  18.     print("-"*30)
  19.     print("对比Sympy的rref结果")
  20.     print(Matrix(augmented).rref(simplify=True))
  21.     print("-"*30)

测试书中的例子

  1. aug_1_1_1 = [[1, -2, 1, 0],
  2.              [0, 2, -8, 8],
  3.              [5, 0, -5, 10]]
  4. eliminate(aug_1_1_1)
  5. # 1.1 example 3
  6. aug_1_1_3 = [[0, 1, -4, 8],
  7.              [2, -3, 2, 1],
  8.              [4, -8, 12, 1]]
  9. eliminate(aug_1_1_3)
  10. eliminate([[1, -6, 4, 0, -1],
  11.            [0, 2, -7, 0, 4],
  12.            [0, 0, 1, 2, -3],
  13.            [0, 0, 3, 1, 6]])
  14. eliminate([[0, -3, -6, 4, 9],
  15.            [-1, -2, -1, 3, 1],
  16.            [-2, -3, 0, 3, -1],
  17.            [1, 4, 5, -9, -7]])
  19. eliminate([[0, 3, -6, 6, 4, -5],
  20.            [3, -7, 8, -5, 8, 9],
  21.            [3, -9, 12, -9, 6, 15]])
  1. [[ 1 -2  1  0]
  2.  [ 0  2 -8  8]
  3.  [ 5  0 -5 10]]
  4.  The echelon form is
  5.  [[ 1. -2.  1.  0.]
  6.  [ 0.  1. -4.  4.]
  7.  [ 0.  0.  1. -1.]]
  8.  The pivots are:  [(0, 0), (1, 1), (2, 2)]
  9.  Is the solution correct?  True
  10.  Solution:
  11.  [[ 1.  0.  0.  1.]
  12.  [ 0.  1.  0.  0.]
  13.  [ 0.  0.  1. -1.]]
  14. ------------------------------
  15. 对比Sympy的rref结果
  16. (Matrix([
  17. [1, 0, 0,  1],
  18. [0, 1, 0,  0],
  19. [0, 0, 1, -1]]), (0, 1, 2))
  20. ------------------------------
  21. [[ 0  1 -4  8]
  22.  [ 2 -3  2  1]
  23.  [ 4 -8 12  1]]
  24.  The echelon form is
  25.  [[ 1.   -2.    3.    0.25]
  26.  [ 0.    1.   -4.    0.5 ]
  27.  [ 0.    0.    0.    1.  ]]
  28.  The pivots are:  [(0, 0), (1, 1), (2, 3)]
  29.  There is controdictory.
  30.  [[ 1.  0. -5.  0.]
  31.  [ 0.  1. -4.  0.]
  32.  [ 0.  0.  0.  1.]]
  33. ------------------------------
  34. 对比Sympy的rref结果
  35. (Matrix([
  36. [1, 0, -5, 0],
  37. [0, 1, -4, 0],
  38. [0, 0,  0, 1]]), (0, 1, 3))
  39. ------------------------------
  40. [[ 1 -6  4  0 -1]
  41.  [ 0  2 -7  0  4]
  42.  [ 0  0  1  2 -3]
  43.  [ 0  0  3  1  6]]
  44.  The echelon form is
  45.  [[ 1.  -6.   4.   0.  -1. ]
  46.  [ 0.   1.  -3.5  0.   2. ]
  47.  [ 0.   0.   1.   2.  -3. ]
  48.  [-0.  -0.  -0.   1.  -3. ]]
  49.  The pivots are:  [(0, 0), (1, 1), (2, 2), (3, 3)]
  50.  Is the solution correct?  True
  51.  Solution:
  52.  [[ 1.   0.   0.   0.  62. ]
  53.  [ 0.   1.   0.   0.  12.5]
  54.  [ 0.   0.   1.   0.   3. ]
  55.  [-0.  -0.  -0.   1.  -3. ]]
  56. ------------------------------
  57. 对比Sympy的rref结果
  58. (Matrix([
  59. [1, 0, 0, 0,   62],
  60. [0, 1, 0, 0, 25/2],
  61. [0, 0, 1, 0,    3],
  62. [0, 0, 0, 1,   -3]]), (0, 1, 2, 3))
  63. ------------------------------
  64. [[ 0 -3 -6  4  9]
  65.  [-1 -2 -1  3  1]
  66.  [-2 -3  0  3 -1]
  67.  [ 1  4  5 -9 -7]]
  68.  The echelon form is
  69.  [[ 1.   1.5 -0.  -1.5  0.5]
  70.  [-0.   1.   2.  -3.  -3. ]
  71.  [-0.  -0.  -0.   1.  -0. ]
  72.  [ 0.   0.   0.   0.   0. ]]
  73.  The pivots are:  [(0, 0), (1, 1), (2, 3)]
  74.  There are free variables.
  75.  [[ 1.  0. -3.  0.  5.]
  76.  [-0.  1.  2.  0. -3.]
  77.  [-0. -0. -0.  1. -0.]
  78.  [ 0.  0.  0.  0.  0.]]
  79. ------------------------------
  80. 对比Sympy的rref结果
  81. (Matrix([
  82. [1, 0, -3, 0,  5],
  83. [0, 1,  2, 0, -3],
  84. [0, 0,  0, 1,  0],
  85. [0, 0,  0, 0,  0]]), (0, 1, 3))
  86. ------------------------------
  87. [[ 0  3 -6  6  4 -5]
  88.  [ 3 -7  8 -5  8  9]
  89.  [ 3 -9 12 -9  6 15]]
  90.  The echelon form is
  91.  [[ 1.         -2.33333333  2.66666667 -1.66666667  2.66666667  3.        ]
  92.  [ 0.          1.         -2.          2.          1.33333333 -1.66666667]
  93.  [ 0.          0.          0.          0.          1.          4.        ]]
  94.  The pivots are:  [(0, 0), (1, 1), (2, 4)]
  95.  There are free variables.
  96.  [[  1.   0.  -2.   3.   0. -24.]
  97.  [  0.   1.  -2.   2.   0.  -7.]
  98.  [  0.   0.   0.   0.   1.   4.]]
  99. ------------------------------
  100. 对比Sympy的rref结果
  101. (Matrix([
  102. [1, 0, -2, 3, 0, -24],
  103. [0, 1, -2, 2, 0,  -7],
  104. [0, 0,  0, 0, 1,   4]]), (0, 1, 4))
  105. ------------------------------

利用Python学习线性代数 -- 1.1 线性方程组的更多相关文章

  1. 利用python 学习数据分析 (学习二)

    内容学习自: Python for Data Analysis, 2nd Edition         就是这本 纯英文学的很累,对不对取决于百度翻译了 前情提要: 各种方法贴: https://w ...

  2. 利用python 学习数据分析 (学习四)

    内容学习自: Python for Data Analysis, 2nd Edition         就是这本 纯英文学的很累,对不对取决于百度翻译了 前情提要: 各种方法贴: https://w ...

  3. 利用python 学习数据分析 (学习三)

    内容学习自: Python for Data Analysis, 2nd Edition         就是这本 纯英文学的很累,对不对取决于百度翻译了 前情提要: 各种方法贴: https://w ...

  4. 利用python 学习数据分析 (学习一)

    内容学习自: Python for Data Analysis, 2nd Edition         就是这本 纯英文学的很累,对不对取决于百度翻译了 前情提要: 各种方法贴: https://w ...

  5. 利用python进行数据分析——（一）库的学习

    总结一下自己对python常用包:Numpy,Pandas,Matplotlib,Scipy,Scikit-learn 一. Numpy: 标准安装的Python中用列表(list)保存一组值,可以用 ...

  6. Python 数据分析（二 本实验将学习利用 Python 数据聚合与分组运算，时间序列，金融与经济数据应用等相关知识

    Python 数据分析(二) 本实验将学习利用 Python 数据聚合与分组运算,时间序列,金融与经济数据应用等相关知识 第1节 groupby 技术 第2节 数据聚合 第3节 分组级运算和转换 第4 ...

  7. 利用Python实现一个感知机学习算法

    本文主要参考英文教材Python Machine Learning第二章.pdf文档下载链接: https://pan.baidu.com/s/1nuS07Qp 密码: gcb9. 本文主要内容包括利 ...

  8. 爬虫学习笔记（1）-- 利用Python从网页抓取数据

    最近想从一个网站上下载资源,懒得一个个的点击下载了,想写一个爬虫把程序全部下载下来,在这里做一个简单的记录 Python的基础语法在这里就不多做叙述了,黑马程序员上有一个基础的视频教学,可以跟着学习一 ...

  9. PYTHON学习（三）之利用python进行数据分析(1)---准备工作

    学习一门语言就是不断实践,python是目前用于数据分析最流行的语言,我最近买了本书<利用python进行数据分析>(Wes McKinney著),还去图书馆借了本<Python数据 ...

随机推荐

  1. java学习1-初始java程序

    # 第一个简单示例 public class Hello { public static void main(String[] args) { System.out.println("Hel ...

  2. Linux面试题-7

    在日常管理中,通常CPU会影响系统性能的情况是: A A:CPU已满负荷地运转 B:CPU的运行效率为30% C:CPU的运行效率为50% D:CPU的运行效率为80% 下面那个命令可以终止一个用户的 ...

  3. Uipath 选择页面下拉列表中的选项

    http://www.rpatokyo.com/ 使用Select item Activity选择页面下拉列表中的选项 在open browser中拖入Select Item Activity,配置参 ...

  4. ESP8266开发之旅 网络篇⑯ 无线更新——OTA固件更新

    授人以鱼不如授人以渔,目的不是为了教会你具体项目开发,而是学会学习的能力.希望大家分享给你周边需要的朋友或者同学,说不定大神成长之路有博哥的奠基石... QQ技术互动交流群:ESP8266&3 ...

  5. Visual Studio Code 添加C/C++编译功能

    VS Code作为一个文本/代码编辑器,相较于VS比较轻量化,而且可以支持C/C++.Python等多种语言,并具有丰富的拓展模块. 但是作为一个编辑器,在VS Code上安装C/C++模块之后,并不 ...

  6. 防抖与节流 & 若每个请求必须发送，如何平滑地获取最后一个接口返回的数据

    博客地址:https://ainyi.com/79 日常浏览网页中,在进行窗口的 resize.scroll 或者重复点击某按钮发送请求,此时事件处理函数或者接口调用的频率若无限制,则会加重浏览器的负 ...

  7. django-模板之include标签（十五）

    就是将一些常用的html代码分离出来,使其可以重复利用,减少代码量 index.html <!DOCTYPE html> <html lang="en"> ...

  8. ubuntu18.04 flink-1.9.0 Standalone集群搭建

    集群规划 Master JobManager Standby JobManager Task Manager Zookeeper flink01 √ √ flink02 √ √ flink03 √ √ ...

  9. 又到了卸载Notepad++的时候了？

    逛开源中国(OSCHINA),无意中发现一贴<不用Notepad++,你还有这些更好的选择> 才发现,原来 Notepad++ 的作者侯今吾前几天又在 npp 的官网上发表了一篇个人政治意 ...

  10. Scrapy 实现爬取多页数据 + 多层url数据爬取

    项目需求:爬取https://www.4567tv.tv/frim/index1.html网站前三页的电影名称和电影的导演名称 项目分析:电影名称在初次发的url返回的response中可以获取,可以 ...