poj3321（dfs序+树状数组）

题目链接：https://vjudge.net/problem/POJ-3321

题意：给一个普通树（不是二叉树），并且已经编号，每个结点为1或0，有两种操作，对单个结点修改和查询一个结点的子树的所有结点的值。

思路：操作为单点操作和区间查询，很适合用树状数组或线段树来解，但是这里的区间查询并不具备减法规则，一个结点的子数的所有结点编号也不连续。

　　　所以需要我们自己来重新给结点编号。这里利用dfs对树遍历一遍，使用一个时间戳（从1开始），在遍历一个结点开始和结束分别记录时间戳s[i],e[i]，能够发现s[i]即为结点i的新编号，s[i]~e[i]即为结点i的管辖范围（就是以i为根的子数的所有结点编号所在区间）。文字描述很抽象，下面举个例子：

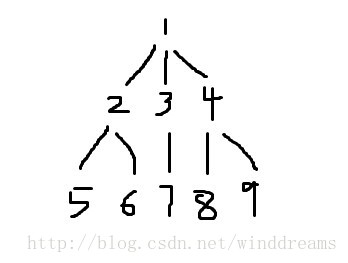
对于上面所示树，数字为题目给的编号。dfs的遍历顺序为

i:　　　　   1      2       5       6      3       7      4      8      9

(s[i],e[i])　   (1,9) (2,4) (3,3) (4,4) (5,6) (6,6) (7,9) (8,8) (9,9)

遍历结点开始时的时间戳表示结点编号这个很自然，遍历完这个结点的子树之后的时间戳其实就是子树结点的最后一个编号，所以s[i]~e[i]表示其子树的编号区间，一个子树的编号也是连续的。

然后就可以利用树状数组来解决剩下的问题了，对单点进行修改，对一个结点的子树进行查询，结果就是query(e[i])-query(s[i]-1)。复杂度为O(nlogn)。

AC代码：

#include<cstdio>
using namespace std;
const int maxn=;

struct node{
    int v,next;
}edge[maxn<<];

int head[maxn],tr[maxn],s[maxn],e[maxn];
bool vis[maxn],a[maxn];
int n,m,cnt,tim;

void add(int u,int v){
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}

void dfs(int p){
    s[p]=++tim;
    vis[p]=;
    for(int i=head[p];i!=-;i=edge[i].next){
        if(vis[edge[i].v]) continue;
        dfs(edge[i].v);
    }
    e[p]=tim;
}

int lowbit(int x){
    return x&(-x);
}

void update(int x,int num){
    while(x<=n){
        tr[x]+=num;
        x+=lowbit(x);
    }
}

int query(int x){
    int ans=;
    while(x>){
        ans+=tr[x];
        x-=lowbit(x);
    }
    return ans;
}

int main(){
    scanf("%d",&n);
    for(int i=;i<=n;++i){
        head[i]=-;
        a[i]=;
        update(i,);
    }
    for(int i=;i<n;++i){
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v);
        add(v,u);
    }
    dfs();
    scanf("%d",&m);
    char c;
    int t;
    while(m--){
        scanf(" %c%d",&c,&t);
        if(c=='C'){
            if(a[t]){
                a[t]=;
                update(s[t],-);
            }
            else{
                a[t]=;
                update(s[t],);
            }
        }
        else{
            printf("%d\n",query(e[t])-query(s[t]-));
        }
    }
    return ;
}