P3749 [六省联考2017]寿司餐厅最小割

$\color{#0066ff}{ 题目描述 }$

Kiana 最近喜欢到一家非常美味的寿司餐厅用餐。

每天晚上，这家餐厅都会按顺序提供 $n$ 种寿司，第 $i$ 种寿司有一个代号 $a_i$ 和美味度 $d_{i, i}$ ，不同种类的寿司有可能使用相同的代号。每种寿司的份数都是无限的，$Kiana$ 也可以无限次取寿司来吃，但每种寿司每次只能取一份，且每次取走的寿司必须是按餐厅提供寿司的顺序连续的一段，即 $Kiana$ 可以一次取走第 $1, 2$ 种寿司各一份，也可以一次取走第 $2, 3$ 种寿司各一份，但不可以一次取走第 $1, 3$ 种寿司。

由于餐厅提供的寿司种类繁多，而不同种类的寿司之间相互会有影响：三文鱼寿司和鱿鱼寿司一起吃或许会很棒，但和水果寿司一起吃就可能会肚子痛。因此，$Kiana$ 定义了一个综合美味度 $d_{i, j} \ (i < j)$，表示在一次取的寿司中，如果包含了餐厅提供的从第 $i$ 份到第 $j$ 份的所有寿司，吃掉这次取的所有寿司后将获得的额外美味度。由于取寿司需要花费一些时间，所以我们认为分两次取来的寿司之间相互不会影响。注意在吃一次取的寿司时，不止一个综合美味度会被累加，比如若 $Kiana$ 一次取走了第 $1, 2, 3$ 种寿司各一份，除了 $d_{1, 3}$ 以外，$d_{1, 2}, d_{2, 3}$ 也会被累加进总美味度中。

神奇的是，$Kiana$ 的美食评判标准是有记忆性的，无论是单种寿司的美味度，还是多种寿司组合起来的综合美味度，在计入 $Kiana$ 的总美味度时都只会被累加一次。比如，若 $Kiana$ 某一次取走了第 $1, 2$ 种寿司各一份，另一次取走了第 $2, 3$种寿司各一份，那么这两次取寿司的总美味度为 $d_{1, 1} + d_{2, 2} + d_{3, 3} + d_{1, 2} + d_{2, 3}$，其中 $d_{2, 2}$ 只会计算一次。

奇怪的是，这家寿司餐厅的收费标准很不同寻常。具体来说，如果 $Kiana$ 一共吃过了 $c \ (c > 0)$ 种代号为 $x$ 的寿司，则她需要为这些寿司付出 $mx^2 + cx$ 元钱，其中 $m$ 是餐厅给出的一个常数。

现在 $Kiana$ 想知道，在这家餐厅吃寿司，自己能获得的总美味度（包括所有吃掉的单种寿司的美味度和所有被累加的综合美味度）减去花费的总钱数的最大值是多少。由于她不会算，所以希望由你告诉她。

$\color{#0066ff}{输入格式}$

第一行包含两个正整数 $n, m$，分别表示这家餐厅提供的寿司总数和计算寿司价格中使用的常数。第二行包含 $n$ 个正整数，其中第 $k$ 个数 $a_k$ 表示第 $k$ 份寿司的代号。接下来 $n$ 行，第 $i$ 行包含 $n - i + 1$ 个整数，其中第 $j$ 个数 $d_{i, i+j-1}$ 表示吃掉寿司能获得的相应的美味度，具体含义见问题描述。

$\color{#0066ff}{输出格式}$

输出共一行包含一个正整数，表示 $Kiana$ 能获得的总美味度减去花费的总钱数的最大值。

$\color{#0066ff}{输入样例}$

10 1

5 5 4 4 1 2 5 1 5 3

83 91 72 29 22 -5 57 -14 -36 -3

-11 34 45 96 32 73 -1 0 29

-48 68 44 -5 96 66 17 74

88 47 69 -9 2 25 -49

86 -9 -77 62 -10 -30

2 40 95 -74 46

49 -52 2 -51

-55 50 -44

72 22

-68

$\color{#0066ff}{输出样例}$

$\color{#0066ff}{数据范围与提示}$

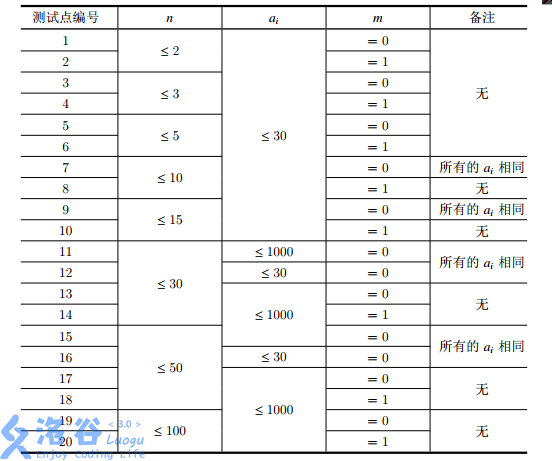
$\color{#0066ff}{题解}$

这是一个最大流最小割的题

要找最大的美味度-花费

我们找到总美味度，用最小割求花费，一减就行了

首先考虑总美味度的问题

因为有负的美味度

考虑将其算在花费里就行了，因为我们并不知道总美味度里到底包不包括某些负的值

将其算作花费在网络流上跑，这样才能保证最大

下面开始花式建边

建边

1、原点向每个美味度为正的区间连容量为美味度的边

2、每个美味度为负的区间像汇点连容量为-美味度的边

3、每个区间$[i,j]$向区间$[i+1,j], [i,j-1]$连一条容量为inf的边

4、每个区间向区间端点对应的寿司连一条inf的边

5、每个寿司向汇点连容量为寿司种类编号的边

6、每个寿司向所属寿司种类连容量为inf的边

7、每个寿司种类向汇点连容量为$m * id * id$的边

#include<bits/stdc++.h>

#define LL long long

LL in() {

	char ch; int x = 0, f = 1;

	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);

	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));

	return x * f;

}

struct node {

	int to, dis;

	node *nxt, *rev;

	node(int to = 0, int dis = 0, node *nxt = NULL): to(to), dis(dis), nxt(nxt) {}

	void *operator new (size_t) {

		static node *S = NULL, *T = NULL;

		return (S == T) && (T = (S = new node[1024]) + 1024), S++;

	}

};

const int maxn = 10505;

const int mod = 150;

const int inf = 0x7fffffff;

int id[mod][mod], val[mod][mod], idd[maxn];

int dep[maxn], a[mod];

node *head[maxn], *cur[maxn];

int n, s, t, m;

int ans;

using std::queue;

queue<int> q;

void add(int from, int to, int dis) {

	head[from] = new node(to, dis, head[from]);

}

void link(int from, int to, int dis) {

	add(from, to, dis);

	add(to, from, 0);

	head[from]->rev = head[to];

	head[to]->rev = head[from];

}

bool bfs() {

	for(int i = s; i <= t; i++) cur[i] = head[i], dep[i] = 0;

	q.push(s);

	dep[s] = 1;

	while(!q.empty()) {

		int tp = q.front(); q.pop();

		for(node *i = head[tp]; i; i = i->nxt)

			if(!dep[i->to] && i->dis) {

				dep[i->to] = dep[tp] + 1;

				q.push(i->to);

			}

	}

	return dep[t];

}

int dfs(int x, int change) {

	if(x == t || !change) return change;

	int flow = 0, ls;

	for(node *i = cur[x]; i; i = i->nxt) {

		cur[x] = i;

		if(dep[i->to] == dep[x] + 1 && (ls = dfs(i->to, std::min(change, i->dis)))) {

			flow += ls;

			change -= ls;

			i->dis -= ls;

			i->rev->dis += ls;

			if(!change) break;

		}

	}

	return flow;

}

int dinic() {

	int flow = 0;

	while(bfs()) flow += dfs(s, inf);

	return flow;

}

void build() {

	int cnt = 0;

	for(int i = 1; i <= n; i++)

		for(int j = i; j <= n; j++)

			id[i][j] = ++cnt;

	static bool vis[maxn];

	for(int i = 1; i <= n; i++)

		if(!vis[a[i]]) {

			vis[a[i]] = true;

			idd[a[i]] = ++cnt;

		}

	memset(vis, 0, sizeof vis);

	s = 0, t = cnt + n + 1;

	for(int i = 1; i <= n; i++)

		if(!vis[a[i]]) {

			vis[a[i]] = true;

			link(idd[a[i]], t, m * a[i] * a[i]);

		}

	for(int i = 1; i <= n; i++) {

		link(cnt + i, idd[a[i]], inf);

		link(cnt + i, t, a[i]);

	}

	for(int i = 1; i <= n; i++)

		for(int j = i; j <= n; j++) {

			if(val[i][j] >= 0) {

				ans += val[i][j];

				link(s, id[i][j], val[i][j]);

				link(id[i][j], cnt + i, inf);

				link(id[i][j], cnt + j, inf);

			}

			else {

				link(id[i][j], t, -val[i][j]);

				link(id[i][j], cnt + i, inf);

				link(id[i][j], cnt + j, inf);

			}

			if(i != j) {

				link(id[i][j], id[i + 1][j], inf);

				link(id[i][j], id[i][j - 1], inf);

			}

		}

}

int main() {

	n = in(), m = in();

	for(int i = 1; i <= n; i++) a[i] = in();

	for(int i = 1; i <= n; i++)

		for(int j = i; j <= n; j++)

			val[i][j] = in();

	build();

	printf("%d", ans - dinic());

	return 0;

}

思想很危险，目前还停留在noip，看到$n\leq 100$,居然只想到了DP，而且还不会写，网络流啊。。。